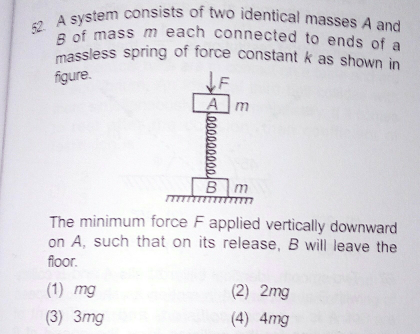
Question Number 26924 by Tinkutara last updated on 31/Dec/17
Answered by mrW1 last updated on 31/Dec/17
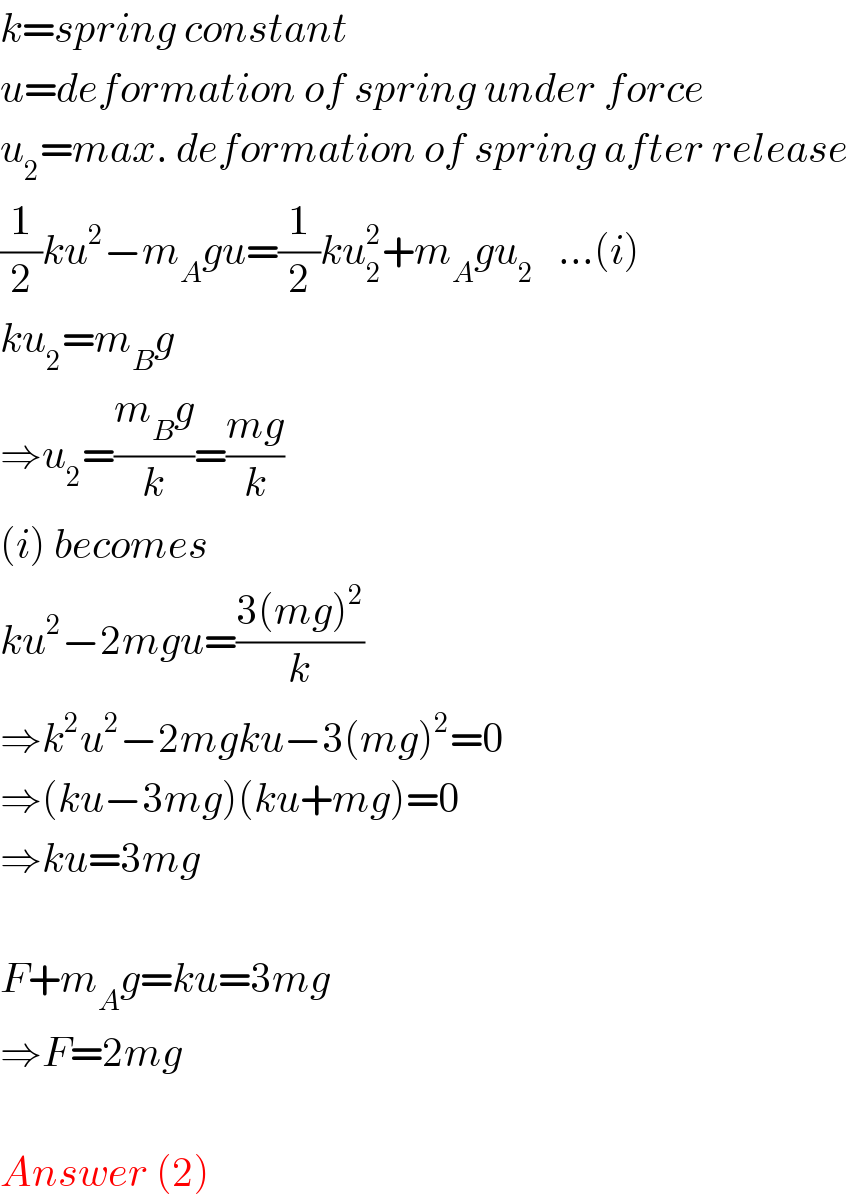
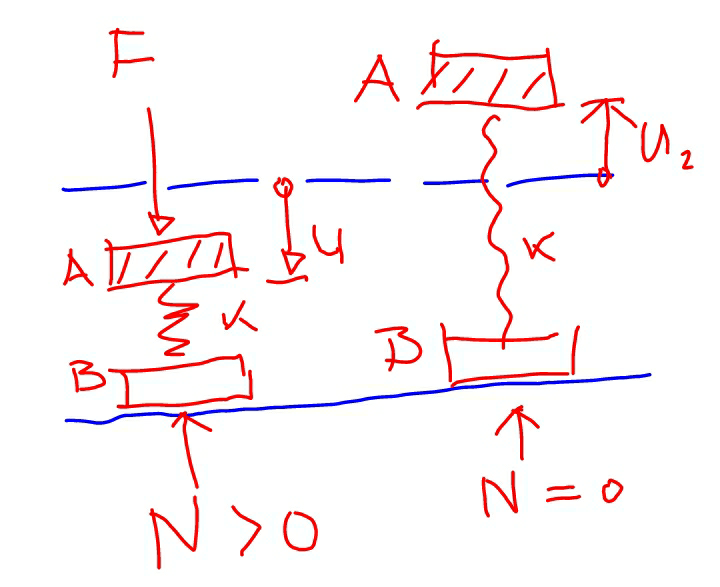
$${k}={spring}\:{constant} \\ $$$${u}={deformation}\:{of}\:{spring}\:{under}\:{force} \\ $$$${u}_{\mathrm{2}} ={max}.\:{deformation}\:{of}\:{spring}\:{after}\:{release} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}{ku}^{\mathrm{2}} −{m}_{{A}} {gu}=\frac{\mathrm{1}}{\mathrm{2}}{ku}_{\mathrm{2}} ^{\mathrm{2}} +{m}_{{A}} {gu}_{\mathrm{2}} \:\:\:…\left({i}\right) \\ $$$${ku}_{\mathrm{2}} ={m}_{{B}} {g} \\ $$$$\Rightarrow{u}_{\mathrm{2}} =\frac{{m}_{{B}} {g}}{{k}}=\frac{{mg}}{{k}} \\ $$$$\left({i}\right)\:{becomes} \\ $$$${ku}^{\mathrm{2}} −\mathrm{2}{mgu}=\frac{\mathrm{3}\left({mg}\right)^{\mathrm{2}} }{{k}} \\ $$$$\Rightarrow{k}^{\mathrm{2}} {u}^{\mathrm{2}} −\mathrm{2}{mgku}−\mathrm{3}\left({mg}\right)^{\mathrm{2}} =\mathrm{0} \\ $$$$\Rightarrow\left({ku}−\mathrm{3}{mg}\right)\left({ku}+{mg}\right)=\mathrm{0} \\ $$$$\Rightarrow{ku}=\mathrm{3}{mg} \\ $$$$ \\ $$$${F}+{m}_{{A}} {g}={ku}=\mathrm{3}{mg} \\ $$$$\Rightarrow{F}=\mathrm{2}{mg} \\ $$$$ \\ $$$${Answer}\:\left(\mathrm{2}\right) \\ $$
Commented by mrW1 last updated on 31/Dec/17
Commented by Tinkutara last updated on 31/Dec/17
Thank you very much Sir! I got the answer.
