Question Number 26951 by Tinkutara last updated on 31/Dec/17

Answered by prakash jain last updated on 31/Dec/17
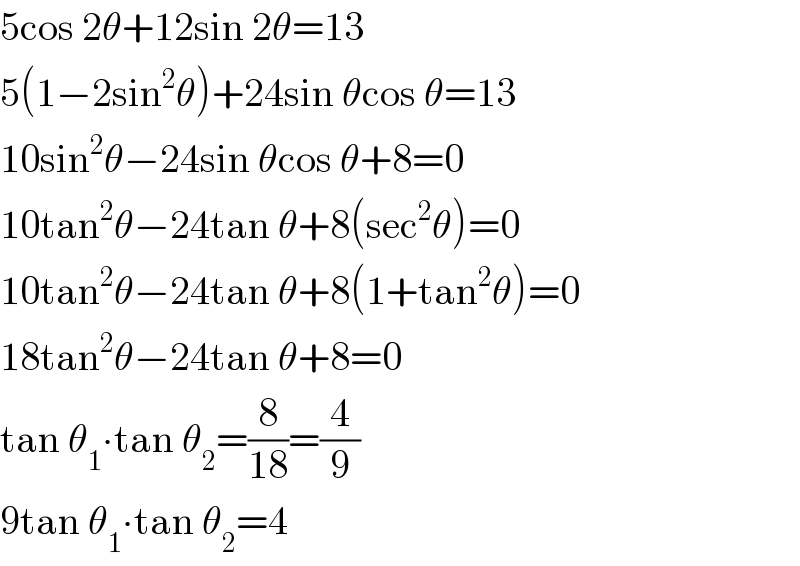
$$\mathrm{5cos}\:\mathrm{2}\theta+\mathrm{12sin}\:\mathrm{2}\theta=\mathrm{13} \\ $$$$\mathrm{5}\left(\mathrm{1}−\mathrm{2sin}^{\mathrm{2}} \theta\right)+\mathrm{24sin}\:\theta\mathrm{cos}\:\theta=\mathrm{13} \\ $$$$\mathrm{10sin}^{\mathrm{2}} \theta−\mathrm{24sin}\:\theta\mathrm{cos}\:\theta+\mathrm{8}=\mathrm{0} \\ $$$$\mathrm{10tan}^{\mathrm{2}} \theta−\mathrm{24tan}\:\theta+\mathrm{8}\left(\mathrm{sec}^{\mathrm{2}} \theta\right)=\mathrm{0} \\ $$$$\mathrm{10tan}^{\mathrm{2}} \theta−\mathrm{24tan}\:\theta+\mathrm{8}\left(\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \theta\right)=\mathrm{0} \\ $$$$\mathrm{18tan}^{\mathrm{2}} \theta−\mathrm{24tan}\:\theta+\mathrm{8}=\mathrm{0} \\ $$$$\mathrm{tan}\:\theta_{\mathrm{1}} \centerdot\mathrm{tan}\:\theta_{\mathrm{2}} =\frac{\mathrm{8}}{\mathrm{18}}=\frac{\mathrm{4}}{\mathrm{9}} \\ $$$$\mathrm{9tan}\:\theta_{\mathrm{1}} \centerdot\mathrm{tan}\:\theta_{\mathrm{2}} =\mathrm{4} \\ $$
Commented by Tinkutara last updated on 31/Dec/17
Thank you very much Sir! I got the answer.
