Question Number 26952 by Femmy last updated on 31/Dec/17
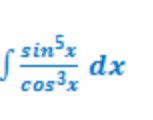
Answered by prakash jain last updated on 31/Dec/17
![∫((sin^5 x)/(cos^3 x))dx=∫((sin^4 x)/(cos^3 x))sin xdx =∫(((1−cos^2 x)^2 )/(cos^3 x))sin xdx =∫((1−2cos^2 x+cos^4 x)/(cos^3 x))sin xdx cos x=u⇒−sin xdx=du =−∫((1/u^3 )−(2/u)+u)du =−[−(1/(2u^2 ))−2ln u+(u^2 /2)]+c =−[−(1/(2cos^2 x))−2ln cos x+((cos^2 x)/2)]+c](https://www.tinkutara.com/question/Q26955.png)
$$\int\frac{\mathrm{sin}^{\mathrm{5}} {x}}{\mathrm{cos}^{\mathrm{3}} {x}}{dx}=\int\frac{\mathrm{sin}^{\mathrm{4}} {x}}{\mathrm{cos}^{\mathrm{3}} {x}}\mathrm{sin}\:{xdx} \\ $$$$=\int\frac{\left(\mathrm{1}−\mathrm{cos}^{\mathrm{2}} {x}\right)^{\mathrm{2}} }{\mathrm{cos}^{\mathrm{3}} {x}}\mathrm{sin}\:{xdx} \\ $$$$=\int\frac{\mathrm{1}−\mathrm{2cos}^{\mathrm{2}} {x}+\mathrm{cos}^{\mathrm{4}} {x}}{\mathrm{cos}^{\mathrm{3}} {x}}\mathrm{sin}\:{xdx} \\ $$$$\mathrm{cos}\:{x}={u}\Rightarrow−\mathrm{sin}\:{xdx}={du} \\ $$$$=−\int\left(\frac{\mathrm{1}}{{u}^{\mathrm{3}} }−\frac{\mathrm{2}}{{u}}+{u}\right){du} \\ $$$$=−\left[−\frac{\mathrm{1}}{\mathrm{2}{u}^{\mathrm{2}} }−\mathrm{2ln}\:{u}+\frac{{u}^{\mathrm{2}} }{\mathrm{2}}\right]+{c} \\ $$$$=−\left[−\frac{\mathrm{1}}{\mathrm{2cos}^{\mathrm{2}} \:{x}}−\mathrm{2ln}\:\mathrm{cos}\:{x}+\frac{\mathrm{cos}^{\mathrm{2}} {x}}{\mathrm{2}}\right]+{c} \\ $$
Commented by Femmy last updated on 31/Dec/17

$$\mathrm{thanks}\:\mathrm{sir}\:\mathrm{but}\:\mathrm{check}\:\mathrm{your}\:\mathrm{ans}\:\mathrm{again}\:\mathrm{little}\:\mathrm{mistake} \\ $$$$\mathrm{8o} \\ $$
Commented by prakash jain last updated on 31/Dec/17
$$\mathrm{Thanks}.\:\mathrm{corrected} \\ $$
