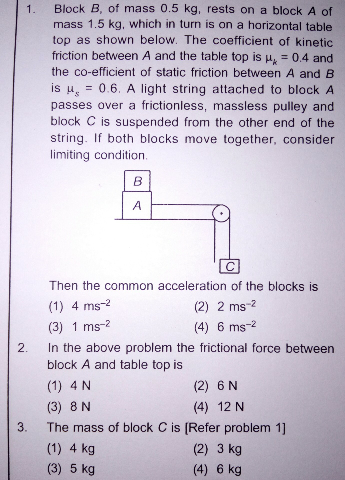
Question Number 26982 by Tinkutara last updated on 31/Dec/17
Answered by mrW1 last updated on 31/Dec/17
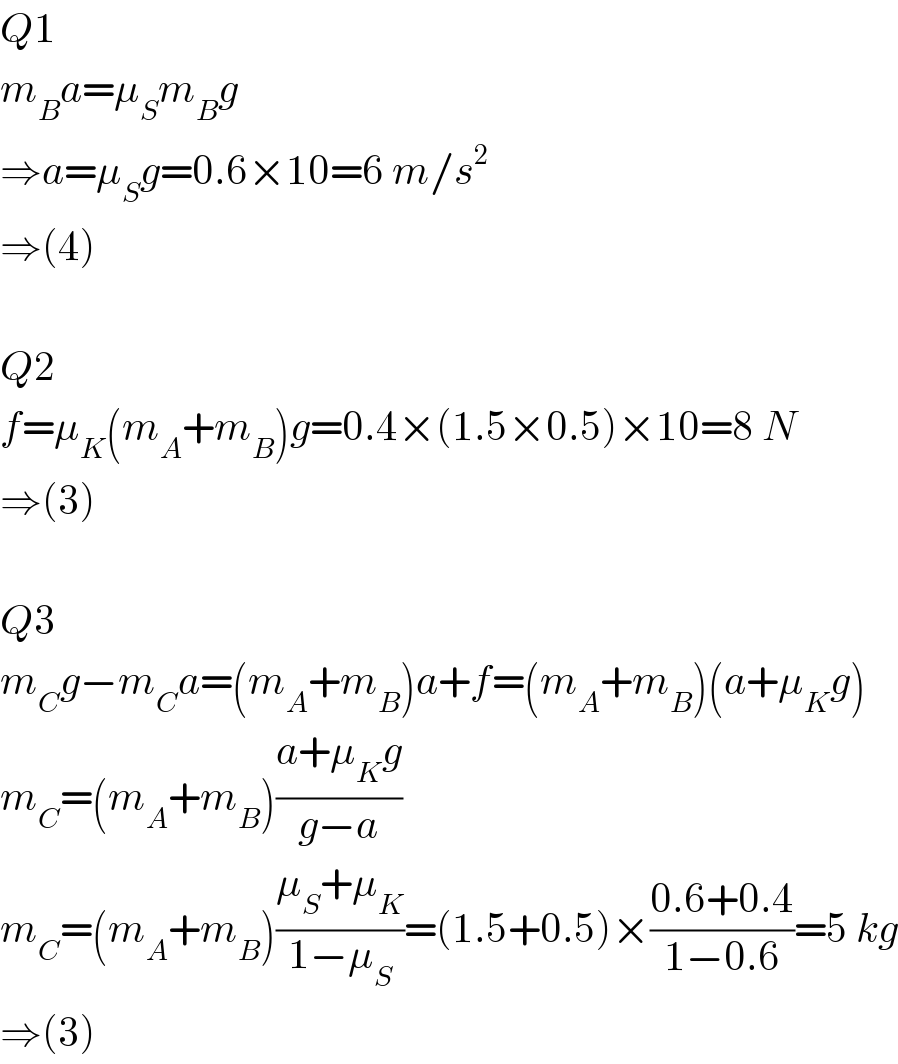
$${Q}\mathrm{1} \\ $$$${m}_{{B}} {a}=\mu_{{S}} {m}_{{B}} {g} \\ $$$$\Rightarrow{a}=\mu_{{S}} {g}=\mathrm{0}.\mathrm{6}×\mathrm{10}=\mathrm{6}\:{m}/{s}^{\mathrm{2}} \\ $$$$\Rightarrow\left(\mathrm{4}\right) \\ $$$$ \\ $$$${Q}\mathrm{2} \\ $$$${f}=\mu_{{K}} \left({m}_{{A}} +{m}_{{B}} \right){g}=\mathrm{0}.\mathrm{4}×\left(\mathrm{1}.\mathrm{5}×\mathrm{0}.\mathrm{5}\right)×\mathrm{10}=\mathrm{8}\:{N} \\ $$$$\Rightarrow\left(\mathrm{3}\right) \\ $$$$ \\ $$$${Q}\mathrm{3} \\ $$$${m}_{{C}} {g}−{m}_{{C}} {a}=\left({m}_{{A}} +{m}_{{B}} \right){a}+{f}=\left({m}_{{A}} +{m}_{{B}} \right)\left({a}+\mu_{{K}} {g}\right) \\ $$$${m}_{{C}} =\left({m}_{{A}} +{m}_{{B}} \right)\frac{{a}+\mu_{{K}} {g}}{{g}−{a}} \\ $$$${m}_{{C}} =\left({m}_{{A}} +{m}_{{B}} \right)\frac{\mu_{{S}} +\mu_{{K}} }{\mathrm{1}−\mu_{{S}} }=\left(\mathrm{1}.\mathrm{5}+\mathrm{0}.\mathrm{5}\right)×\frac{\mathrm{0}.\mathrm{6}+\mathrm{0}.\mathrm{4}}{\mathrm{1}−\mathrm{0}.\mathrm{6}}=\mathrm{5}\:{kg} \\ $$$$\Rightarrow\left(\mathrm{3}\right) \\ $$
Commented by Tinkutara last updated on 01/Jan/18
But in first question there is written that consider limiting friction. So why we take 0.6 then?
Commented by mrW1 last updated on 01/Jan/18

$${The}\:{limiting}\:{condition}\:{that}\:{block}\:{A} \\ $$$${and}\:{B}\:{move}\:{together}\:{is}\:{that}\:{the} \\ $$$${acceleration}\:{of}\:{them}\:{is}\:{not}\:{more} \\ $$$${than}\:{the}\:{max}.\:{static}\:{friction}\:{can} \\ $$$${reach},\:{that}\:{is}\:{a}_{{max}} =\mu_{{s}} {g}.\:{if}\:{the} \\ $$$${acceleration}\:{is}\:{bigger}\:{than}\:{this},\:{block} \\ $$$${B}\:{will}\:{slip}. \\ $$
Commented by mrW1 last updated on 01/Jan/18
There are following situations:
0< mc ≦0.8 kg: no motion, a=0.
0.8 < mc ≦ 5 kg: block A and B move together, 0<a≦6 m/s2.
mc > 5 kg: block B slips over block A, aA>6m/s2,aB=6m/s2.
Commented by Tinkutara last updated on 03/Jan/18
Thank you very much Sir! I got the answer.
