Question Number 27002 by math solver last updated on 01/Jan/18
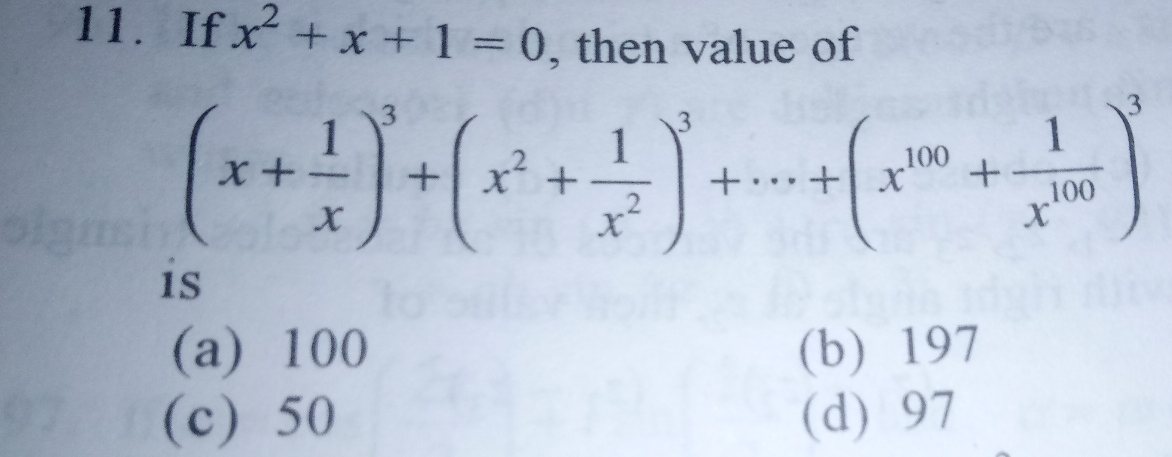
Commented by moxhix last updated on 01/Jan/18

$${x}\neq\mathrm{0}\:\left(\because\mathrm{0}^{\mathrm{2}} +\mathrm{0}+\mathrm{1}\neq\mathrm{0}\right) \\ $$$$\frac{{x}^{\mathrm{2}} +{x}+\mathrm{1}}{{x}}=\frac{\mathrm{0}}{{x}} \\ $$$${x}+\frac{\mathrm{1}}{{x}}=−\mathrm{1} \\ $$$$… \\ $$
Commented by math solver last updated on 01/Jan/18
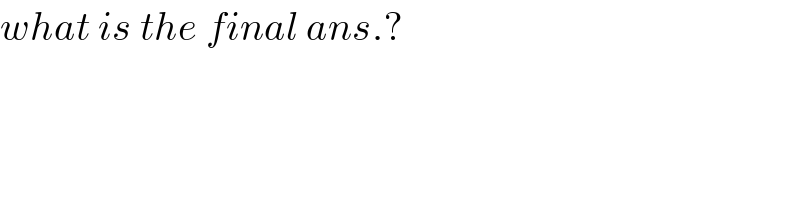
$${what}\:{is}\:{the}\:{final}\:{ans}.? \\ $$
Commented by abdo imad last updated on 01/Jan/18
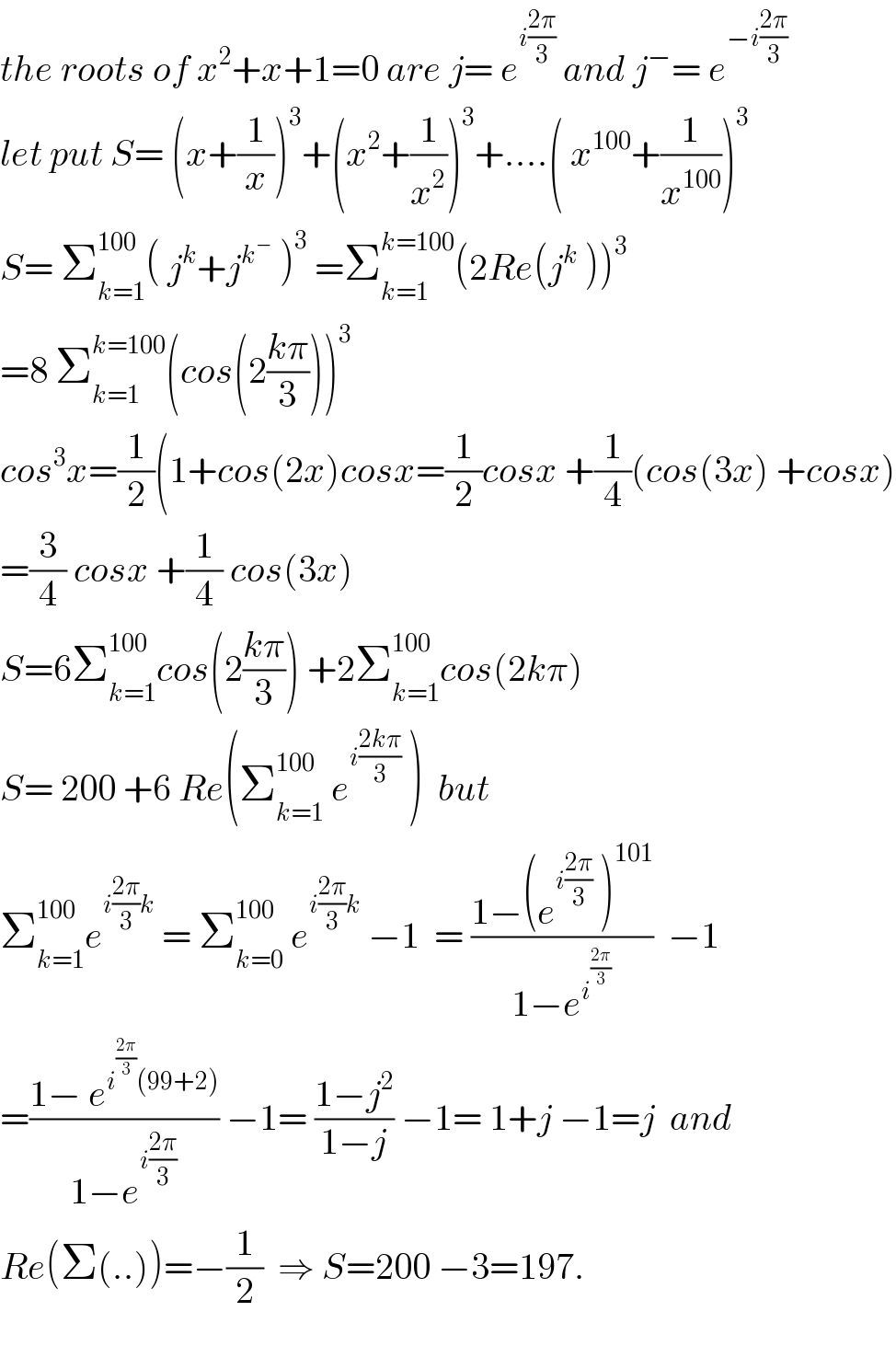
$${the}\:{roots}\:{of}\:{x}^{\mathrm{2}} +{x}+\mathrm{1}=\mathrm{0}\:{are}\:{j}=\:{e}^{{i}\frac{\mathrm{2}\pi}{\mathrm{3}}} \:{and}\:{j}^{−} =\:{e}^{−{i}\frac{\mathrm{2}\pi}{\mathrm{3}}} \\ $$$${let}\:{put}\:{S}=\:\left({x}+\frac{\mathrm{1}}{{x}}\right)^{\mathrm{3}} +\left({x}^{\mathrm{2}} +\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\right)^{\mathrm{3}} +….\left(\:{x}^{\mathrm{100}} +\frac{\mathrm{1}}{{x}^{\mathrm{100}} }\right)^{\mathrm{3}} \\ $$$${S}=\:\sum_{{k}=\mathrm{1}} ^{\mathrm{100}} \left(\:{j}^{{k}} +{j}^{{k}^{−} } \:\right)^{\mathrm{3}} \:=\sum_{{k}=\mathrm{1}} ^{{k}=\mathrm{100}} \left(\mathrm{2}{Re}\left({j}^{{k}} \:\right)\right)^{\mathrm{3}} \\ $$$$=\mathrm{8}\:\sum_{{k}=\mathrm{1}} ^{{k}=\mathrm{100}} \left({cos}\left(\mathrm{2}\frac{{k}\pi}{\mathrm{3}}\right)\right)^{\mathrm{3}} \\ $$$${cos}^{\mathrm{3}} {x}=\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{1}+{cos}\left(\mathrm{2}{x}\right){cosx}=\frac{\mathrm{1}}{\mathrm{2}}{cosx}\:+\frac{\mathrm{1}}{\mathrm{4}}\left({cos}\left(\mathrm{3}{x}\right)\:+{cosx}\right)\right. \\ $$$$=\frac{\mathrm{3}}{\mathrm{4}}\:{cosx}\:+\frac{\mathrm{1}}{\mathrm{4}}\:{cos}\left(\mathrm{3}{x}\right) \\ $$$${S}=\mathrm{6}\sum_{{k}=\mathrm{1}} ^{\mathrm{100}} {cos}\left(\mathrm{2}\frac{{k}\pi}{\mathrm{3}}\right)\:+\mathrm{2}\sum_{{k}=\mathrm{1}} ^{\mathrm{100}} {cos}\left(\mathrm{2}{k}\pi\right) \\ $$$${S}=\:\mathrm{200}\:+\mathrm{6}\:{Re}\left(\sum_{{k}=\mathrm{1}} ^{\mathrm{100}} \:{e}^{{i}\frac{\mathrm{2}{k}\pi}{\mathrm{3}}} \:\right)\:\:{but} \\ $$$$\sum_{{k}=\mathrm{1}} ^{\mathrm{100}} {e}^{{i}\frac{\mathrm{2}\pi}{\mathrm{3}}{k}} \:=\:\sum_{{k}=\mathrm{0}} ^{\mathrm{100}} \:{e}^{{i}\frac{\mathrm{2}\pi}{\mathrm{3}}{k}} \:−\mathrm{1}\:\:=\:\frac{\mathrm{1}−\left({e}^{{i}\frac{\mathrm{2}\pi}{\mathrm{3}}} \:\right)^{\mathrm{101}} }{\mathrm{1}−{e}^{{i}^{\frac{\mathrm{2}\pi}{\mathrm{3}}} } }\:\:−\mathrm{1} \\ $$$$=\frac{\mathrm{1}−\:{e}^{{i}^{\frac{\mathrm{2}\pi}{\mathrm{3}}} \left(\mathrm{99}+\mathrm{2}\right)} }{\mathrm{1}−{e}^{{i}\frac{\mathrm{2}\pi}{\mathrm{3}}} }\:−\mathrm{1}=\:\frac{\mathrm{1}−{j}^{\mathrm{2}} }{\mathrm{1}−{j}}\:−\mathrm{1}=\:\mathrm{1}+{j}\:−\mathrm{1}={j}\:\:{and}\: \\ $$$${Re}\left(\Sigma\left(..\right)\right)=−\frac{\mathrm{1}}{\mathrm{2}}\:\:\Rightarrow\:{S}=\mathrm{200}\:−\mathrm{3}=\mathrm{197}. \\ $$$$ \\ $$
Commented by abdo imad last updated on 01/Jan/18

$${S}=\mathrm{200}−\mathrm{3}=\:\mathrm{197}\:. \\ $$
Answered by AHSoomro last updated on 01/Jan/18

$$\mathrm{x}^{\mathrm{2}} +\mathrm{x}+\mathrm{1}=\mathrm{0} \\ $$$${x}=\frac{−\mathrm{1}\pm\sqrt{\mathrm{1}−\mathrm{4}}}{\mathrm{2}}=\frac{−\mathrm{1}\pm\mathrm{i}\sqrt{\mathrm{3}}}{\mathrm{2}} \\ $$$$\:\:=\omega,\omega^{\mathrm{2}} \\ $$$$\mathrm{Let}\:\mathrm{x}=\omega \\ $$$$\left(\omega+\frac{\mathrm{1}}{\omega}\right)^{\mathrm{3}} +\left(\omega^{\mathrm{2}} +\frac{\mathrm{1}}{\omega^{\mathrm{2}} }\right)^{\omega} +…+\left(\omega^{\mathrm{100}} +\frac{\mathrm{1}}{\omega^{\mathrm{100}} }\right)^{\mathrm{3}} \\ $$$$\left(\omega+\omega^{−\mathrm{1}} \right)^{\mathrm{3}} +\left(\omega^{\mathrm{2}} +\omega^{−\mathrm{2}} \right)^{\mathrm{3}} +…\left(\omega^{\mathrm{100}} +\omega^{−\mathrm{100}} \right) \\ $$$$\omega^{\mathrm{n}} +\omega^{−\mathrm{n}} =? \\ $$$$\mathrm{n}\:\mathrm{may}\:\mathrm{be}\:\mathrm{one}\:\mathrm{of}\:\mathrm{3k},\mathrm{3k}+\mathrm{1},\mathrm{3k}+\mathrm{2} \\ $$$$\:^{\bullet} \mathrm{n}=\mathrm{3k}\Rightarrow\omega^{\mathrm{n}} +\omega^{−\mathrm{n}} =\omega^{\mathrm{3k}} +\omega^{−\mathrm{3k}} \\ $$$$=\left(\omega^{\mathrm{3}} \right)^{\mathrm{k}} +\left(\omega^{\mathrm{3}} \right)^{−\mathrm{k}} =\mathrm{1}^{\mathrm{k}} +\mathrm{1}^{−\mathrm{k}} =\mathrm{2} \\ $$$$\:^{\bullet} \mathrm{n}=\mathrm{3k}+\mathrm{1}\Rightarrow\omega^{\mathrm{3k}+\mathrm{1}} +\omega^{−\left(\mathrm{3k}+\mathrm{1}\right)} \\ $$$$\:\:=\left(\omega^{\mathrm{3}} \right)^{\mathrm{k}} \omega+\left(\omega^{\mathrm{3}} \right)^{−\mathrm{k}} \omega^{−\mathrm{1}} =\omega+\omega^{−\mathrm{1}} \\ $$$$\:\:=\omega+\omega^{\mathrm{2}} =−\mathrm{1} \\ $$$$\:^{\bullet} \mathrm{n}=\mathrm{3k}+\mathrm{2}\Rightarrow\omega^{\mathrm{3k}+\mathrm{2}} +\omega^{−\left(\mathrm{3k}+\mathrm{2}\right)} \\ $$$$\:\:\:\:\:\:=\omega^{\mathrm{2}} +\omega^{−\mathrm{2}} =\omega^{\mathrm{2}} +\omega=−\mathrm{1} \\ $$$$\left(\omega^{\mathrm{3k}} +\frac{\mathrm{1}}{\omega^{\mathrm{3k}} }\right)^{\mathrm{3}} \:\:\:\mathrm{33}\:\mathrm{times} \\ $$$$\mathrm{2}^{\mathrm{3}} ×\mathrm{33}=\mathrm{264} \\ $$$$\left(\omega^{\mathrm{3k}+\mathrm{1}} +\frac{\mathrm{1}}{\omega^{\mathrm{3k}+\mathrm{1}} }\right)^{\mathrm{3}} \:\:\mathrm{and}\:\:\left(\omega^{\mathrm{3k}+\mathrm{2}} +\frac{\mathrm{1}}{\omega^{\mathrm{3k}+\mathrm{2}} }\right)^{\mathrm{3}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{67}\:\mathrm{times} \\ $$$$\left(−\mathrm{1}\right)^{\mathrm{3}} ×\mathrm{67}=−\mathrm{67} \\ $$$$\mathrm{2}^{\mathrm{3}} ×\mathrm{33}+\left(−\mathrm{1}\right)^{\mathrm{3}} ×\mathrm{67}=\mathrm{264}−\mathrm{67}=\mathrm{197} \\ $$
Commented by math solver last updated on 01/Jan/18

$${thanks}! \\ $$
Commented by abdo imad last updated on 01/Jan/18
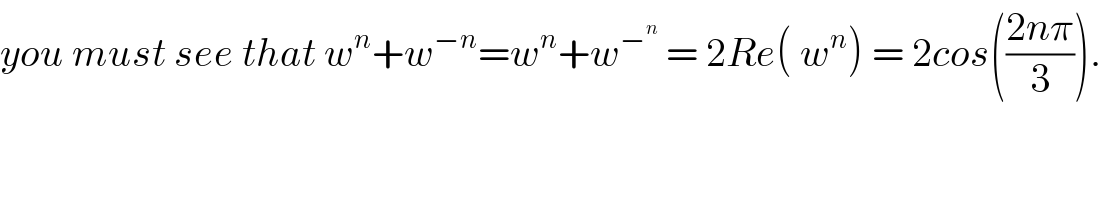
$${you}\:{must}\:{see}\:{that}\:{w}^{{n}} +{w}^{−{n}} ={w}^{{n}} +{w}^{−^{{n}} } \:=\:\mathrm{2}{Re}\left(\:{w}^{{n}} \right)\:=\:\mathrm{2}{cos}\left(\frac{\mathrm{2}{n}\pi}{\mathrm{3}}\right). \\ $$
Commented by Rasheed.Sindhi last updated on 01/Jan/18

$${I}\:{think}\:{Mr}\:{AHSoomro}\:{has}\:{solved}\:{without} \\ $$$${going}\:{into}\:{polar}\:{coordinates}. \\ $$
Commented by abdo imad last updated on 02/Jan/18

$${yes}\:{it}\:{seems}… \\ $$
Answered by ajfour last updated on 01/Jan/18
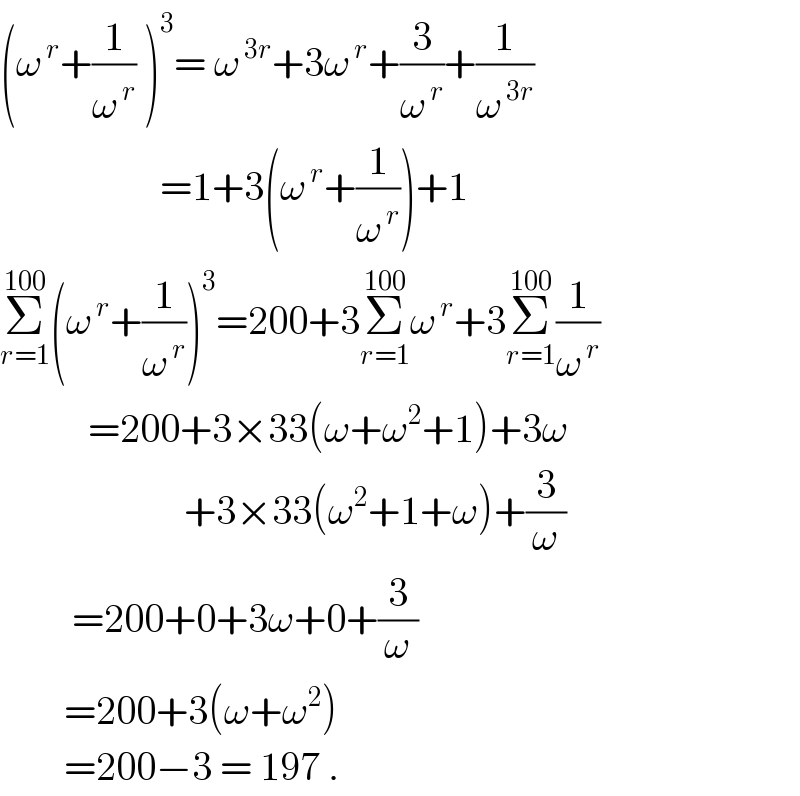
$$\left(\omega^{\:{r}} +\frac{\mathrm{1}}{\omega^{\:{r}} }\:\right)^{\mathrm{3}} =\:\omega^{\:\mathrm{3}{r}} +\mathrm{3}\omega^{\:{r}} +\frac{\mathrm{3}}{\omega^{\:{r}} }+\frac{\mathrm{1}}{\omega^{\:\mathrm{3}{r}} } \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{1}+\mathrm{3}\left(\omega^{\:{r}} +\frac{\mathrm{1}}{\omega^{\:{r}} }\right)+\mathrm{1} \\ $$$$\underset{{r}=\mathrm{1}} {\overset{\mathrm{100}} {\sum}}\left(\omega^{\:{r}} +\frac{\mathrm{1}}{\omega^{\:{r}} }\right)^{\mathrm{3}} =\mathrm{200}+\mathrm{3}\underset{{r}=\mathrm{1}} {\overset{\mathrm{100}} {\sum}}\omega^{\:{r}} +\mathrm{3}\underset{{r}=\mathrm{1}} {\overset{\mathrm{100}} {\sum}}\frac{\mathrm{1}}{\omega^{\:{r}} } \\ $$$$\:\:\:\:\:\:\:\:\:\:\:=\mathrm{200}+\mathrm{3}×\mathrm{33}\left(\omega+\omega^{\mathrm{2}} +\mathrm{1}\right)+\mathrm{3}\omega \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:+\mathrm{3}×\mathrm{33}\left(\omega^{\mathrm{2}} +\mathrm{1}+\omega\right)+\frac{\mathrm{3}}{\omega} \\ $$$$\:\:\:\:\:\:\:\:\:=\mathrm{200}+\mathrm{0}+\mathrm{3}\omega+\mathrm{0}+\frac{\mathrm{3}}{\omega} \\ $$$$\:\:\:\:\:\:\:\:=\mathrm{200}+\mathrm{3}\left(\omega+\omega^{\mathrm{2}} \right) \\ $$$$\:\:\:\:\:\:\:\:=\mathrm{200}−\mathrm{3}\:=\:\mathrm{197}\:. \\ $$
Commented by math solver last updated on 01/Jan/18

$${thank}\:{u}\:{sir}! \\ $$$$ \\ $$
