Question Number 27044 by Tinkutara last updated on 01/Jan/18

Answered by mrW1 last updated on 02/Jan/18

$$\alpha=\mathrm{30}° \\ $$$${x}={u}\:\mathrm{cos}\:\theta\:{t} \\ $$$${y}={u}\:\mathrm{sin}\:\theta\:{t}\:−\frac{{gt}^{\mathrm{2}} }{\mathrm{2}} \\ $$$${by}\:{landing}: \\ $$$${y}={x}\:\mathrm{tan}\:\alpha=\frac{{x}\:\mathrm{sin}\:\alpha}{\mathrm{cos}\:\alpha} \\ $$$${t}_{\mathrm{1}} =\mathrm{3}.\mathrm{5}\:{s} \\ $$$$\Rightarrow{ut}_{\mathrm{1}} \:\mathrm{sin}\:\theta−\frac{{gt}_{\mathrm{1}} ^{\mathrm{2}} }{\mathrm{2}}=\frac{\mathrm{sin}\:\alpha}{\mathrm{cos}\:\alpha}×{ut}_{\mathrm{1}} \:\mathrm{cos}\:\theta \\ $$$$\Rightarrow\mathrm{sin}\:\theta−\frac{{gt}_{\mathrm{1}} }{\mathrm{2}{u}}=\frac{\mathrm{sin}\:\alpha}{\mathrm{cos}\:\alpha}\:\mathrm{cos}\:\theta \\ $$$$\Rightarrow\mathrm{cos}\:\alpha\:\mathrm{sin}\:\theta−\frac{{gt}_{\mathrm{1}} \:\mathrm{cos}\:\alpha}{\mathrm{2}{u}}=\mathrm{sin}\:\alpha\:\mathrm{cos}\:\theta \\ $$$$\Rightarrow\mathrm{cos}\:\alpha\:\mathrm{sin}\:\theta−\mathrm{sin}\:\alpha\:\mathrm{cos}\:\theta=\frac{{gt}_{\mathrm{1}} \:\mathrm{cos}\:\alpha}{\mathrm{2}{u}} \\ $$$$\Rightarrow\mathrm{sin}\:\left(\theta−\:\alpha\right)=\frac{{gt}_{\mathrm{1}} \:\mathrm{cos}\:\alpha}{\mathrm{2}{u}} \\ $$$$\Rightarrow\theta=\:\alpha+\mathrm{sin}^{−\mathrm{1}} \left(\frac{{gt}_{\mathrm{1}} \:\mathrm{cos}\:\alpha}{\mathrm{2}{u}}\right) \\ $$$$\Rightarrow\theta=\:\mathrm{30}+\mathrm{sin}^{−\mathrm{1}} \left(\frac{\mathrm{10}×\mathrm{3}.\mathrm{5}×\mathrm{cos}\:\mathrm{30}°}{\mathrm{2}×\mathrm{53}}\right)=\mathrm{46}.\mathrm{62}° \\ $$$$ \\ $$$${at}\:{t}=\mathrm{2}\:{s}: \\ $$$${u}_{{x}} \left({t}\right)={u}\:\mathrm{cos}\:\theta \\ $$$${u}_{{y}} \left({t}\right)={u}\:\mathrm{sin}\:\theta−{gt} \\ $$$${u}\left({t}\right)=\sqrt{\left({u}\:\mathrm{cos}\:\theta\right)^{\mathrm{2}} +\left({u}\:\mathrm{sin}\:\theta−{gt}\right)^{\mathrm{2}} } \\ $$$${u}\left({t}\right)=\sqrt{{u}^{\mathrm{2}} +{gt}\left({gt}−\mathrm{2}{u}\:\mathrm{sin}\:\theta\right)} \\ $$$${u}\left({t}\right)=\sqrt{\mathrm{53}^{\mathrm{2}} +\mathrm{10}×\mathrm{2}\left(\mathrm{10}×\mathrm{2}−\mathrm{2}×\mathrm{53}×\mathrm{sin}\:\mathrm{46}.\mathrm{62}°\right)}=\mathrm{40}.\mathrm{84}\:{m}/{s} \\ $$$$\Delta{u}=\mathrm{53}−\mathrm{40}.\mathrm{84}=\mathrm{12}.\mathrm{16}\:{m}/{s} \\ $$
Commented by mrW1 last updated on 03/Jan/18
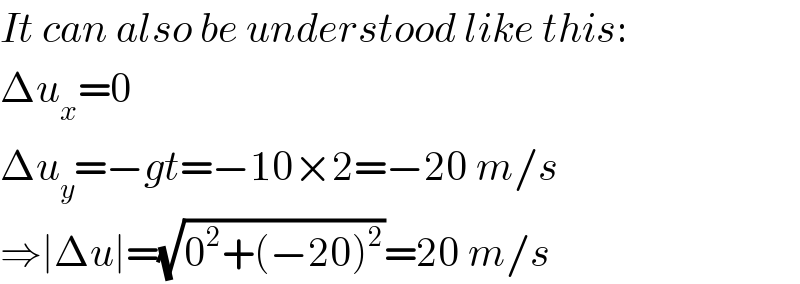
$${It}\:{can}\:{also}\:{be}\:{understood}\:{like}\:{this}: \\ $$$$\Delta{u}_{{x}} =\mathrm{0} \\ $$$$\Delta{u}_{{y}} =−{gt}=−\mathrm{10}×\mathrm{2}=−\mathrm{20}\:{m}/{s} \\ $$$$\Rightarrow\mid\Delta{u}\mid=\sqrt{\mathrm{0}^{\mathrm{2}} +\left(−\mathrm{20}\right)^{\mathrm{2}} }=\mathrm{20}\:{m}/{s} \\ $$
Commented by Tinkutara last updated on 03/Jan/18
Yes answer given is 20 m/s. Thank you very much Sir! I got the answer.
