Question Number 27074 by Tinkutara last updated on 01/Jan/18

Answered by mrW1 last updated on 01/Jan/18

Commented by mrW1 last updated on 02/Jan/18
![dm=λdx=(a_0 +b_0 x^2 )dx dF=((Gmdm)/((a+x)^2 ))=((Gm(a_0 +b_0 x^2 )dx)/((a+x)^2 )) F=∫_0 ^( L) ((Gm(a_0 +b_0 x^2 )dx)/((a+x)^2 )) F=Gm∫_0 ^( L) (((a_0 +b_0 x^2 )dx)/((a+x)^2 )) F=Gm{a_0 [(1/(a+x))]_L ^0 +b_0 ∫_0 ^( L) ((x^2 dx)/((a+x)^2 ))} F=Gm{a_0 ((1/a)−(1/(a+L)))+b_0 [x−2a ln (x+a)−(a^2 /(x+a))]_0 ^L } F=Gm{a_0 ((1/a)−(1/(a+L)))+b_0 (L+2a ln (a/(a+L))+a−(a^2 /(a+L)))} F=Gm{((a_0 L)/(a(a+L)))+b_0 [2a ln (a/(a+L))+(((2a+L)L)/(a+L))]}](https://www.tinkutara.com/question/Q27079.png)
$${dm}=\lambda{dx}=\left({a}_{\mathrm{0}} +{b}_{\mathrm{0}} {x}^{\mathrm{2}} \right){dx} \\ $$$${dF}=\frac{{Gmdm}}{\left({a}+{x}\right)^{\mathrm{2}} }=\frac{{Gm}\left({a}_{\mathrm{0}} +{b}_{\mathrm{0}} {x}^{\mathrm{2}} \right){dx}}{\left({a}+{x}\right)^{\mathrm{2}} } \\ $$$${F}=\int_{\mathrm{0}} ^{\:{L}} \frac{{Gm}\left({a}_{\mathrm{0}} +{b}_{\mathrm{0}} {x}^{\mathrm{2}} \right){dx}}{\left({a}+{x}\right)^{\mathrm{2}} } \\ $$$${F}={Gm}\int_{\mathrm{0}} ^{\:{L}} \frac{\left({a}_{\mathrm{0}} +{b}_{\mathrm{0}} {x}^{\mathrm{2}} \right){dx}}{\left({a}+{x}\right)^{\mathrm{2}} } \\ $$$${F}={Gm}\left\{{a}_{\mathrm{0}} \left[\frac{\mathrm{1}}{{a}+{x}}\right]_{{L}} ^{\mathrm{0}} +{b}_{\mathrm{0}} \int_{\mathrm{0}} ^{\:{L}} \frac{{x}^{\mathrm{2}} {dx}}{\left({a}+{x}\right)^{\mathrm{2}} }\right\} \\ $$$${F}={Gm}\left\{{a}_{\mathrm{0}} \left(\frac{\mathrm{1}}{{a}}−\frac{\mathrm{1}}{{a}+{L}}\right)+{b}_{\mathrm{0}} \left[{x}−\mathrm{2}{a}\:\mathrm{ln}\:\left({x}+{a}\right)−\frac{{a}^{\mathrm{2}} }{{x}+{a}}\right]_{\mathrm{0}} ^{{L}} \right\} \\ $$$${F}={Gm}\left\{{a}_{\mathrm{0}} \left(\frac{\mathrm{1}}{{a}}−\frac{\mathrm{1}}{{a}+{L}}\right)+{b}_{\mathrm{0}} \left({L}+\mathrm{2}{a}\:\mathrm{ln}\:\frac{{a}}{{a}+{L}}+{a}−\frac{{a}^{\mathrm{2}} }{{a}+{L}}\right)\right\} \\ $$$${F}={Gm}\left\{\frac{{a}_{\mathrm{0}} {L}}{{a}\left({a}+{L}\right)}+{b}_{\mathrm{0}} \left[\mathrm{2}{a}\:\mathrm{ln}\:\frac{{a}}{{a}+{L}}+\frac{\left(\mathrm{2}{a}+{L}\right){L}}{{a}+{L}}\right]\right\} \\ $$
Commented by mrW1 last updated on 02/Jan/18
![∫(x^2 /((a+x)^2 ))dx =∫((x^2 +2ax+a^2 −2ax−a^2 )/((a+x)^2 ))dx =∫[1−((2ax+a^2 )/((a+x)^2 ))]dx =∫[1−((2ax+2a^2 −a^2 )/((a+x)^2 ))]dx =x−∫((2a(x+a))/((a+x)^2 ))dx+a^2 ∫(1/((a+x)^2 ))dx =x−2a∫(1/(a+x))dx−(a^2 /(a+x)) =x−2a ln ∣a+x∣−(a^2 /(a+x))+C](https://www.tinkutara.com/question/Q27116.png)
$$\:\int\frac{{x}^{\mathrm{2}} }{\left({a}+{x}\right)^{\mathrm{2}} }{dx} \\ $$$$\:=\int\frac{{x}^{\mathrm{2}} +\mathrm{2}{ax}+{a}^{\mathrm{2}} −\mathrm{2}{ax}−{a}^{\mathrm{2}} }{\left({a}+{x}\right)^{\mathrm{2}} }{dx} \\ $$$$\:=\int\left[\mathrm{1}−\frac{\mathrm{2}{ax}+{a}^{\mathrm{2}} }{\left({a}+{x}\right)^{\mathrm{2}} }\right]{dx} \\ $$$$\:=\int\left[\mathrm{1}−\frac{\mathrm{2}{ax}+\mathrm{2}{a}^{\mathrm{2}} −{a}^{\mathrm{2}} }{\left({a}+{x}\right)^{\mathrm{2}} }\right]{dx} \\ $$$$\:={x}−\int\frac{\mathrm{2}{a}\left({x}+{a}\right)}{\left({a}+{x}\right)^{\mathrm{2}} }{dx}+{a}^{\mathrm{2}} \int\frac{\mathrm{1}}{\left({a}+{x}\right)^{\mathrm{2}} }{dx} \\ $$$$\:={x}−\mathrm{2}{a}\int\frac{\mathrm{1}}{{a}+{x}}{dx}−\frac{{a}^{\mathrm{2}} }{{a}+{x}} \\ $$$$\:={x}−\mathrm{2}{a}\:\mathrm{ln}\:\mid{a}+{x}\mid−\frac{{a}^{\mathrm{2}} }{{a}+{x}}+{C} \\ $$
Commented by Tinkutara last updated on 02/Jan/18
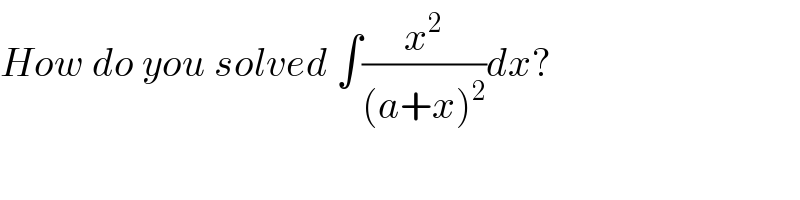
$${How}\:{do}\:{you}\:{solved}\:\int\frac{{x}^{\mathrm{2}} }{\left({a}+{x}\right)^{\mathrm{2}} }{dx}? \\ $$
Commented by Tinkutara last updated on 02/Jan/18
There is slight mistake in ln term. Answer given is:
Commented by Tinkutara last updated on 02/Jan/18

Commented by mrW1 last updated on 02/Jan/18

$${please}\:{recheck}\:{the}\:{answer}\:{in}\:{your}\:{book}. \\ $$$${i}\:{think}\:{the}\:{last}\:{term}\:{should}\:{be} \\ $$$$+\mathrm{2}{ab}_{\mathrm{0}} \:\mathrm{ln}\:\frac{{a}}{{a}+{L}}\:{or} \\ $$$$−\mathrm{2}{ab}_{\mathrm{0}} \:\mathrm{ln}\:\frac{{a}+{L}}{{a}} \\ $$
Commented by mrW1 last updated on 02/Jan/18
![[−2a ln (a+x)]_0 ^L =−2a[ln (a+L)−ln a]=−2a ln ((a+L)/a)=2a ln (a/(a+L))](https://www.tinkutara.com/question/Q27126.png)
$$\:\left[−\mathrm{2}{a}\:\mathrm{ln}\:\left({a}+{x}\right)\right]_{\mathrm{0}} ^{{L}} =−\mathrm{2}{a}\left[\mathrm{ln}\:\left({a}+{L}\right)−\mathrm{ln}\:{a}\right]=−\mathrm{2}{a}\:\mathrm{ln}\:\frac{{a}+{L}}{{a}}=\mathrm{2}{a}\:\mathrm{ln}\:\frac{{a}}{{a}+{L}} \\ $$
Commented by Tinkutara last updated on 03/Jan/18
Thank you very much Sir!
Answered by ajfour last updated on 02/Jan/18
![F=∫_0 ^( L) ((Gm(a_0 +b_0 x^2 )dx)/((x+a)^2 )) =Gm∫_a ^( a+L) (([a_0 +b_0 (t−a)^2 ]dt)/t^2 ) =Gm(−(a_0 /t))∣_a ^(a+L) +b_0 Gm∫_a ^( a+L) [1−((2a)/t)+(a^2 /t^2 )]dt =((Gma_0 L)/(a(a+L)))+b_0 Gm[L−2aln (((a+L)/a))+((a^2 L)/(a(a+L)))] =Gm[((L(a_0 +a^2 b_0 ))/(a(a+L)))+b_0 L−2ab_0 ln (1+(L/a))] .](https://www.tinkutara.com/question/Q27131.png)
$${F}=\int_{\mathrm{0}} ^{\:\:{L}} \frac{{Gm}\left({a}_{\mathrm{0}} +{b}_{\mathrm{0}} {x}^{\mathrm{2}} \right){dx}}{\left({x}+{a}\right)^{\mathrm{2}} } \\ $$$$\:\:={Gm}\int_{{a}} ^{\:\:{a}+{L}} \frac{\left[{a}_{\mathrm{0}} +{b}_{\mathrm{0}} \left({t}−{a}\right)^{\mathrm{2}} \right]{dt}}{{t}^{\mathrm{2}} } \\ $$$$\:={Gm}\left(−\frac{{a}_{\mathrm{0}} }{{t}}\right)\mid_{{a}} ^{{a}+{L}} +{b}_{\mathrm{0}} {Gm}\int_{{a}} ^{\:\:{a}+{L}} \left[\mathrm{1}−\frac{\mathrm{2}{a}}{{t}}+\frac{{a}^{\mathrm{2}} }{{t}^{\mathrm{2}} }\right]{dt} \\ $$$$=\frac{{Gma}_{\mathrm{0}} {L}}{{a}\left({a}+{L}\right)}+{b}_{\mathrm{0}} {Gm}\left[{L}−\mathrm{2}{a}\mathrm{ln}\:\left(\frac{{a}+{L}}{{a}}\right)+\frac{{a}^{\mathrm{2}} {L}}{{a}\left({a}+{L}\right)}\right] \\ $$$$={Gm}\left[\frac{{L}\left({a}_{\mathrm{0}} +{a}^{\mathrm{2}} {b}_{\mathrm{0}} \right)}{{a}\left({a}+{L}\right)}+{b}_{\mathrm{0}} {L}−\mathrm{2}{ab}_{\mathrm{0}} \mathrm{ln}\:\left(\mathrm{1}+\frac{{L}}{{a}}\right)\right]\:. \\ $$
Commented by mrW1 last updated on 02/Jan/18

$${thanks}\:{for}\:{confirming}\:{the}\:{result}! \\ $$
Commented by Tinkutara last updated on 03/Jan/18
Thank you very much Sir!
