Question Number 27112 by NECx last updated on 02/Jan/18
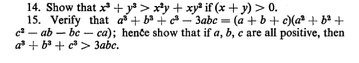
Commented by NECx last updated on 02/Jan/18
$${please}\:{help}\:{with}\:{the}\:{both}…\:{Thanks} \\ $$
Commented by prakash jain last updated on 05/Jan/18
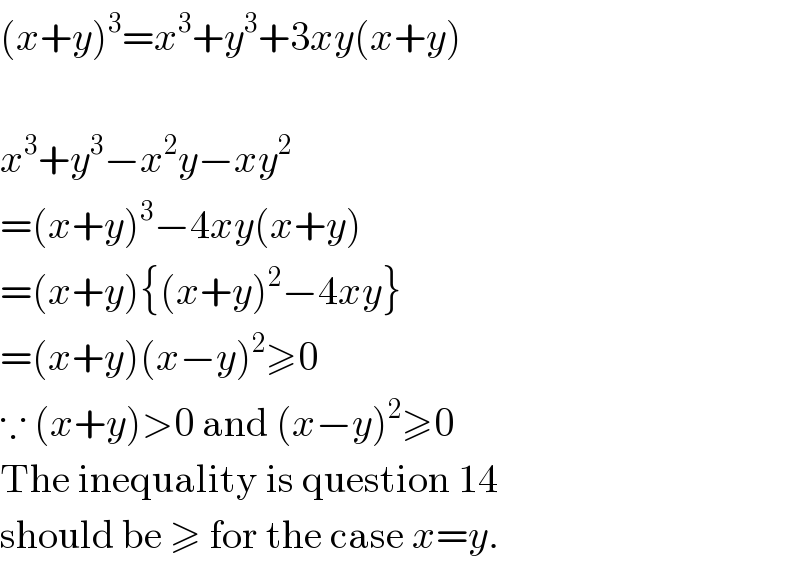
$$\left({x}+{y}\right)^{\mathrm{3}} ={x}^{\mathrm{3}} +{y}^{\mathrm{3}} +\mathrm{3}{xy}\left({x}+{y}\right) \\ $$$$ \\ $$$${x}^{\mathrm{3}} +{y}^{\mathrm{3}} −{x}^{\mathrm{2}} {y}−{xy}^{\mathrm{2}} \\ $$$$=\left({x}+{y}\right)^{\mathrm{3}} −\mathrm{4}{xy}\left({x}+{y}\right) \\ $$$$=\left({x}+{y}\right)\left\{\left({x}+{y}\right)^{\mathrm{2}} −\mathrm{4}{xy}\right\} \\ $$$$=\left({x}+{y}\right)\left({x}−{y}\right)^{\mathrm{2}} \geqslant\mathrm{0} \\ $$$$\because\:\left({x}+{y}\right)>\mathrm{0}\:\mathrm{and}\:\left({x}−{y}\right)^{\mathrm{2}} \geqslant\mathrm{0} \\ $$$$\mathrm{The}\:\mathrm{inequality}\:\mathrm{is}\:\mathrm{question}\:\mathrm{14} \\ $$$$\mathrm{should}\:\mathrm{be}\:\geqslant\:\mathrm{for}\:\mathrm{the}\:\mathrm{case}\:{x}={y}. \\ $$
