Question Number 27202 by Tinkutara last updated on 03/Jan/18
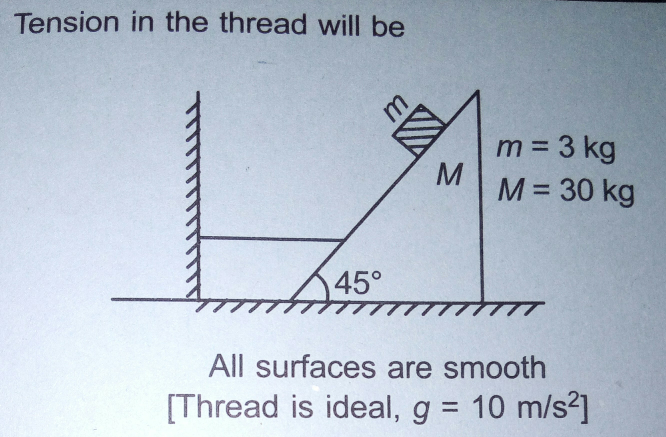
Answered by mrW1 last updated on 03/Jan/18
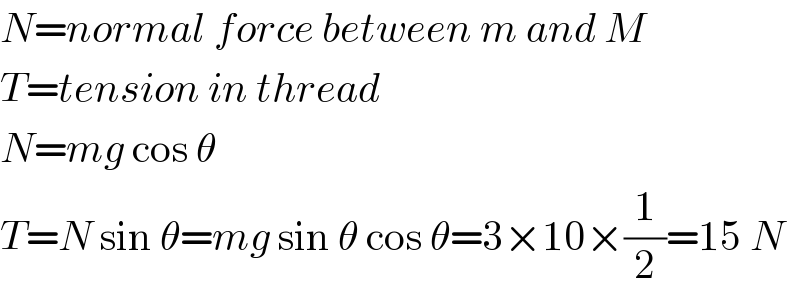
$${N}={normal}\:{force}\:{between}\:{m}\:{and}\:{M} \\ $$$${T}={tension}\:{in}\:{thread} \\ $$$${N}={mg}\:\mathrm{cos}\:\theta \\ $$$${T}={N}\:\mathrm{sin}\:\theta={mg}\:\mathrm{sin}\:\theta\:\mathrm{cos}\:\theta=\mathrm{3}×\mathrm{10}×\frac{\mathrm{1}}{\mathrm{2}}=\mathrm{15}\:{N} \\ $$
Commented by Tinkutara last updated on 03/Jan/18
Why we can't resolve tension along the inclined plane and normal to it and then balance the forces?
Commented by mrW1 last updated on 03/Jan/18
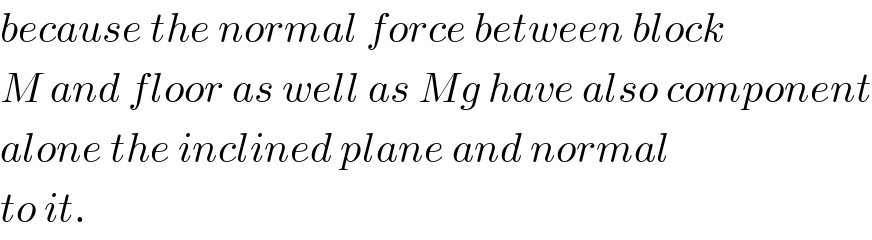
$${because}\:{the}\:{normal}\:{force}\:{between}\:{block} \\ $$$${M}\:{and}\:{floor}\:{as}\:{well}\:{as}\:{Mg}\:{have}\:{also}\:{component} \\ $$$${alone}\:{the}\:{inclined}\:{plane}\:{and}\:{normal} \\ $$$${to}\:{it}. \\ $$
Commented by Tinkutara last updated on 03/Jan/18
Thank you very much Sir! I got the answer.
Commented by mrW1 last updated on 03/Jan/18
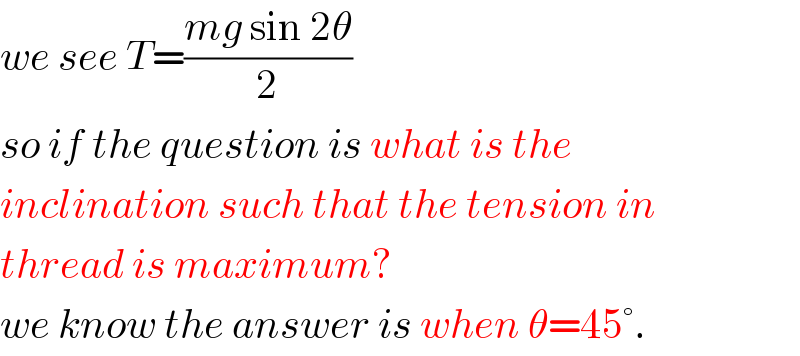
$${we}\:{see}\:{T}=\frac{{mg}\:\mathrm{sin}\:\mathrm{2}\theta}{\mathrm{2}} \\ $$$${so}\:{if}\:{the}\:{question}\:{is}\:{what}\:{is}\:{the} \\ $$$${inclination}\:{such}\:{that}\:{the}\:{tension}\:{in} \\ $$$${thread}\:{is}\:{maximum}? \\ $$$${we}\:{know}\:{the}\:{answer}\:{is}\:{when}\:\theta=\mathrm{45}°. \\ $$
Commented by Tinkutara last updated on 03/Jan/18
Yes thanks Sir.
