Question-27300

Question Number 27300 by mondodotto@gmail.com last updated on 04/Jan/18

Commented by mondodotto@gmail.com last updated on 04/Jan/18

$$\mathrm{any}\:\mathrm{one}\:\mathrm{to}\:\mathrm{help}\:\mathrm{this}\:\mathrm{please} \\ $$

Answered by bsayani309@gmail.com last updated on 05/Jan/18

if we think that 3=x then the sequence may be (x/(x+2)).((2(x+2))/(2(x+2)−2)).((2[2(x+2)−2])/(2[2(x+2)−2]+2)) like this the 5th term becoms((68)/(70)) and the 6th term is ((140)/(138))

$${if}\:{we}\:{think}\:{that}\:\mathrm{3}={x}\:{then}\:{the}\:{sequence}\:{may}\:{be}\: \\ $$$$\frac{{x}}{{x}+\mathrm{2}}.\frac{\mathrm{2}\left({x}+\mathrm{2}\right)}{\mathrm{2}\left({x}+\mathrm{2}\right)−\mathrm{2}}.\frac{\mathrm{2}\left[\mathrm{2}\left(\boldsymbol{{x}}+\mathrm{2}\right)−\mathrm{2}\right]}{\mathrm{2}\left[\mathrm{2}\left(\boldsymbol{{x}}+\mathrm{2}\right)−\mathrm{2}\right]+\mathrm{2}} \\ $$$$\boldsymbol{{like}}\:\boldsymbol{{this}}\:\boldsymbol{{the}}\:\mathrm{5}\boldsymbol{{th}}\:\boldsymbol{{term}}\:\boldsymbol{{becoms}}\frac{\mathrm{68}}{\mathrm{70}}\:\boldsymbol{{and}}\:\boldsymbol{{the}}\:\mathrm{6}\boldsymbol{{th}}\:\boldsymbol{{term}}\:\boldsymbol{{is}}\:\frac{\mathrm{140}}{\mathrm{138}} \\ $$

Answered by prakash jain last updated on 05/Jan/18

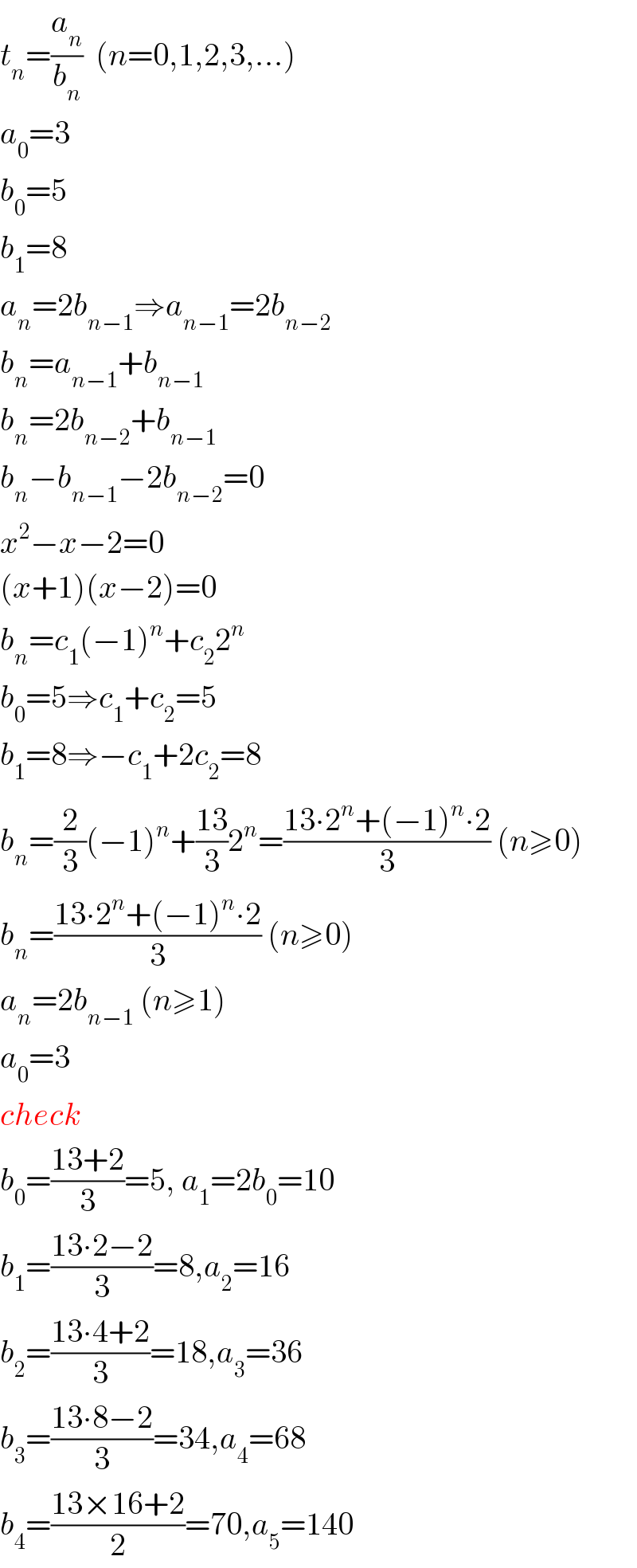
t_n =(a_n /b_n ) (n=0,1,2,3,...) a_0 =3 b_0 =5 b_1 =8 a_n =2b_(n−1) ⇒a_(n−1) =2b_(n−2) b_n =a_(n−1) +b_(n−1) b_n =2b_(n−2) +b_(n−1) b_n −b_(n−1) −2b_(n−2) =0 x^2 −x−2=0 (x+1)(x−2)=0 b_n =c_1 (−1)^n +c_2 2^n b_0 =5⇒c_1 +c_2 =5 b_1 =8⇒−c_1 +2c_2 =8 b_n =(2/3)(−1)^n +((13)/3)2^n =((13∙2^n +(−1)^n ∙2)/3) (n≥0) b_n =((13∙2^n +(−1)^n ∙2)/3) (n≥0) a_n =2b_(n−1) (n≥1) a_0 =3 check b_0 =((13+2)/3)=5, a_1 =2b_0 =10 b_1 =((13∙2−2)/3)=8,a_2 =16 b_2 =((13∙4+2)/3)=18,a_3 =36 b_3 =((13∙8−2)/3)=34,a_4 =68 b_4 =((13×16+2)/2)=70,a_5 =140

$${t}_{{n}} =\frac{{a}_{{n}} }{{b}_{{n}} }\:\:\left({n}=\mathrm{0},\mathrm{1},\mathrm{2},\mathrm{3},…\right) \\ $$$${a}_{\mathrm{0}} =\mathrm{3} \\ $$$${b}_{\mathrm{0}} =\mathrm{5} \\ $$$${b}_{\mathrm{1}} =\mathrm{8} \\ $$$${a}_{{n}} =\mathrm{2}{b}_{{n}−\mathrm{1}} \Rightarrow{a}_{{n}−\mathrm{1}} =\mathrm{2}{b}_{{n}−\mathrm{2}} \\ $$$${b}_{{n}} ={a}_{{n}−\mathrm{1}} +{b}_{{n}−\mathrm{1}} \\ $$$${b}_{{n}} =\mathrm{2}{b}_{{n}−\mathrm{2}} +{b}_{{n}−\mathrm{1}} \\ $$$${b}_{{n}} −{b}_{{n}−\mathrm{1}} −\mathrm{2}{b}_{{n}−\mathrm{2}} =\mathrm{0} \\ $$$${x}^{\mathrm{2}} −{x}−\mathrm{2}=\mathrm{0} \\ $$$$\left({x}+\mathrm{1}\right)\left({x}−\mathrm{2}\right)=\mathrm{0} \\ $$$${b}_{{n}} ={c}_{\mathrm{1}} \left(−\mathrm{1}\right)^{{n}} +{c}_{\mathrm{2}} \mathrm{2}^{{n}} \\ $$$${b}_{\mathrm{0}} =\mathrm{5}\Rightarrow{c}_{\mathrm{1}} +{c}_{\mathrm{2}} =\mathrm{5} \\ $$$${b}_{\mathrm{1}} =\mathrm{8}\Rightarrow−{c}_{\mathrm{1}} +\mathrm{2}{c}_{\mathrm{2}} =\mathrm{8} \\ $$$${b}_{{n}} =\frac{\mathrm{2}}{\mathrm{3}}\left(−\mathrm{1}\right)^{{n}} +\frac{\mathrm{13}}{\mathrm{3}}\mathrm{2}^{{n}} =\frac{\mathrm{13}\centerdot\mathrm{2}^{{n}} +\left(−\mathrm{1}\right)^{{n}} \centerdot\mathrm{2}}{\mathrm{3}}\:\left({n}\geqslant\mathrm{0}\right) \\ $$$${b}_{{n}} =\frac{\mathrm{13}\centerdot\mathrm{2}^{{n}} +\left(−\mathrm{1}\right)^{{n}} \centerdot\mathrm{2}}{\mathrm{3}}\:\left({n}\geqslant\mathrm{0}\right) \\ $$$${a}_{{n}} =\mathrm{2}{b}_{{n}−\mathrm{1}} \:\left({n}\geqslant\mathrm{1}\right) \\ $$$${a}_{\mathrm{0}} =\mathrm{3} \\ $$$${check} \\ $$$${b}_{\mathrm{0}} =\frac{\mathrm{13}+\mathrm{2}}{\mathrm{3}}=\mathrm{5},\:{a}_{\mathrm{1}} =\mathrm{2}{b}_{\mathrm{0}} =\mathrm{10} \\ $$$${b}_{\mathrm{1}} =\frac{\mathrm{13}\centerdot\mathrm{2}−\mathrm{2}}{\mathrm{3}}=\mathrm{8},{a}_{\mathrm{2}} =\mathrm{16} \\ $$$${b}_{\mathrm{2}} =\frac{\mathrm{13}\centerdot\mathrm{4}+\mathrm{2}}{\mathrm{3}}=\mathrm{18},{a}_{\mathrm{3}} =\mathrm{36} \\ $$$${b}_{\mathrm{3}} =\frac{\mathrm{13}\centerdot\mathrm{8}−\mathrm{2}}{\mathrm{3}}=\mathrm{34},{a}_{\mathrm{4}} =\mathrm{68} \\ $$$${b}_{\mathrm{4}} =\frac{\mathrm{13}×\mathrm{16}+\mathrm{2}}{\mathrm{2}}=\mathrm{70},{a}_{\mathrm{5}} =\mathrm{140} \\ $$

Commented by mondodotto@gmail.com last updated on 05/Jan/18

$$\mathrm{thanx}\:\mathrm{a}\:\mathrm{lot}\:\mathrm{really}\:\mathrm{apreciate}\:\mathrm{this} \\ $$

Commented by Rasheed.Sindhi last updated on 05/Jan/18

$$\boldsymbol{{e}}^{\boldsymbol{\mathcal{X}}} \boldsymbol{{celent}}\:\boldsymbol{{Sir}}! \\ $$

Answered by shiv15031973@gmail.com last updated on 05/Jan/18

as every denominator double is next no. numerator ∵34+34=68 and every fraction is having difference at up down of 2 in sequence so next denominator will be70 ans=((68)/(70)) and((140)/(138)) .

$${as}\:{every}\:{denominator}\:{double}\:{is} \\ $$$${next}\:{no}.\:{numerator}\:\because\mathrm{34}+\mathrm{34}=\mathrm{68} \\ $$$${and}\:{every}\:{fraction}\:{is}\:{having}\:{difference} \\ $$$${at}\:{up}\:{down}\:{of}\:\mathrm{2}\:{in}\:{sequence}\: \\ $$$$\boldsymbol{{so}}\:\boldsymbol{{next}}\:\boldsymbol{{denominator}}\:\boldsymbol{{will}}\:\boldsymbol{{be}}\mathrm{70} \\ $$$$\boldsymbol{{ans}}=\frac{\mathrm{68}}{\mathrm{70}}\:\:\boldsymbol{{and}}\frac{\mathrm{140}}{\mathrm{138}}\:. \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply