Question Number 27303 by Tinkutara last updated on 04/Jan/18

Answered by mrW1 last updated on 05/Jan/18
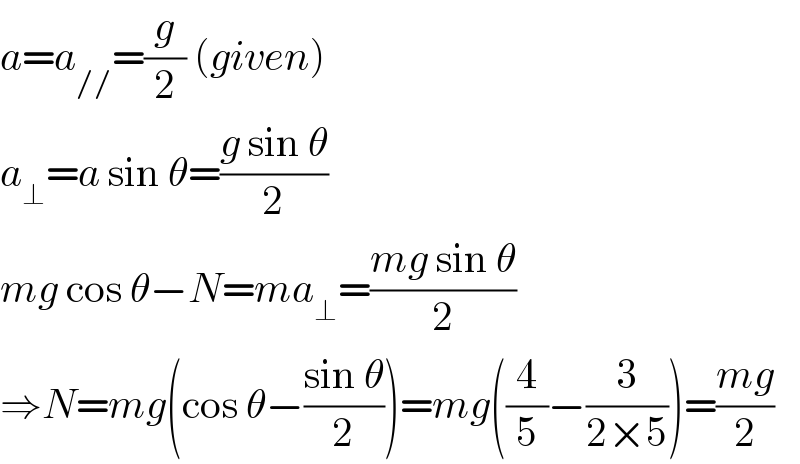
$${a}={a}_{//} =\frac{{g}}{\mathrm{2}}\:\left({given}\right) \\ $$$${a}_{\bot} ={a}\:\mathrm{sin}\:\theta=\frac{{g}\:\mathrm{sin}\:\theta}{\mathrm{2}} \\ $$$${mg}\:\mathrm{cos}\:\theta−{N}={ma}_{\bot} =\frac{{mg}\:\mathrm{sin}\:\theta}{\mathrm{2}} \\ $$$$\Rightarrow{N}={mg}\left(\mathrm{cos}\:\theta−\frac{\mathrm{sin}\:\theta}{\mathrm{2}}\right)={mg}\left(\frac{\mathrm{4}}{\mathrm{5}}−\frac{\mathrm{3}}{\mathrm{2}×\mathrm{5}}\right)=\frac{{mg}}{\mathrm{2}} \\ $$
Commented by mrW1 last updated on 05/Jan/18
Commented by Tinkutara last updated on 05/Jan/18

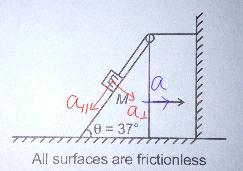
$${Why}\:{a}_{\bot} ={a}\mathrm{sin}\:\theta? \\ $$
Commented by mrW1 last updated on 05/Jan/18

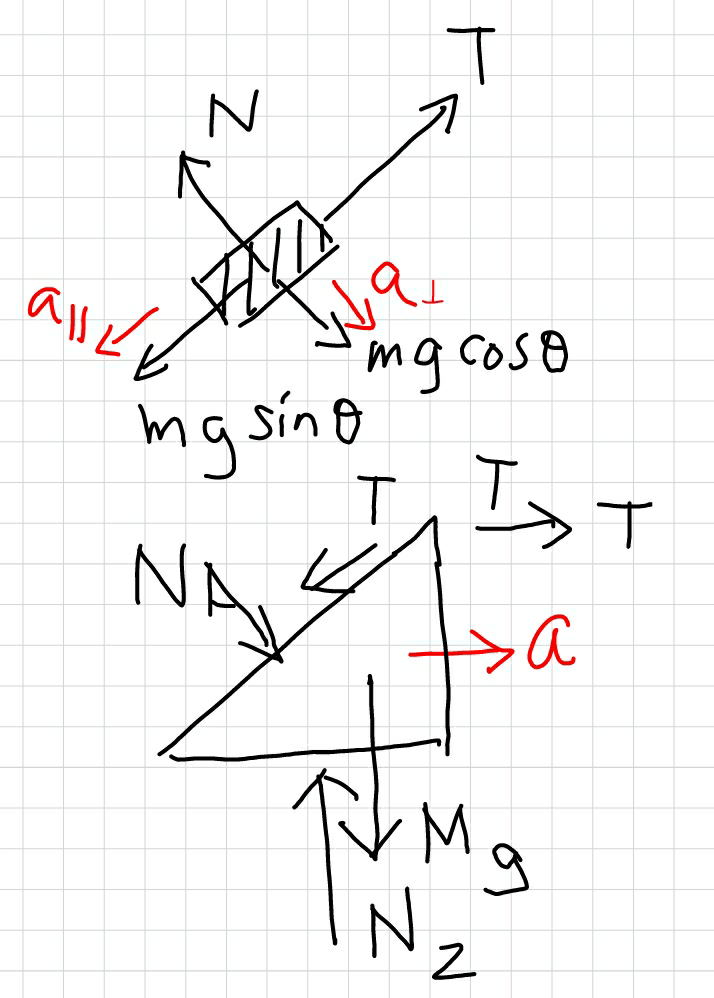
$${the}\:{component}\:{of}\:{a}\:{from}\:{M}\:{in}\:{direction}\:{normal} \\ $$$${to}\:{the}\:{contact}\:{surface}\:{is}\:{a}\:\mathrm{sin}\:\theta,\:{which} \\ $$$${must}\:{be}\:{the}\:{same}\:{as}\:{a}_{\bot} \:{from}\:{m}. \\ $$
Commented by mrW1 last updated on 05/Jan/18
Commented by mrW1 last updated on 05/Jan/18

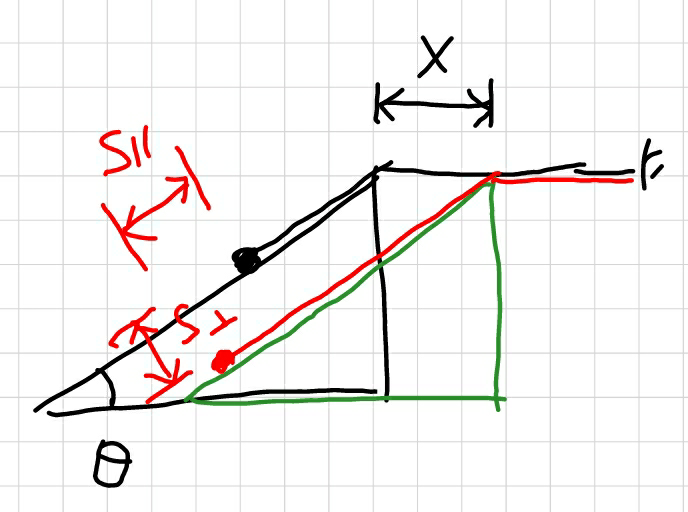
$${let}\:{x}={displacement}\:{of}\:{wedge}\:{M} \\ $$$${acceleration}\:{of}\:{block}\:{M}\:{is}\:{a}=\frac{{d}^{\mathrm{2}} {x}}{{dt}^{\mathrm{2}} } \\ $$$${displacement}\:{of}\:{block}\:{m}\:{is} \\ $$$${s}_{//} ={x} \\ $$$${s}_{\bot} ={x}\:\mathrm{sin}\:\theta \\ $$$$\Rightarrow{a}_{//} =\frac{{d}^{\mathrm{2}} {s}_{//} }{{dt}^{\mathrm{2}} }={a} \\ $$$$\Rightarrow{a}_{\bot} =\frac{{d}^{\mathrm{2}} {s}_{\bot} }{{dt}^{\mathrm{2}} }={a}\:\mathrm{sin}\:\theta \\ $$
Commented by Tinkutara last updated on 05/Jan/18
Then why the relative acceleration of block is g/2 w.r.t wedge?
Commented by mrW1 last updated on 05/Jan/18
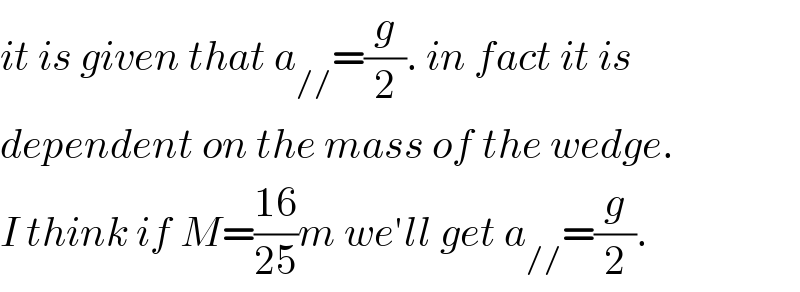
$${it}\:{is}\:{given}\:{that}\:{a}_{//} =\frac{{g}}{\mathrm{2}}.\:{in}\:{fact}\:{it}\:{is} \\ $$$${dependent}\:{on}\:{the}\:{mass}\:{of}\:{the}\:{wedge}. \\ $$$${I}\:{think}\:{if}\:{M}=\frac{\mathrm{16}}{\mathrm{25}}{m}\:{we}'{ll}\:{get}\:{a}_{//} =\frac{{g}}{\mathrm{2}}. \\ $$
Commented by mrW1 last updated on 05/Jan/18
Commented by Tinkutara last updated on 05/Jan/18
Thank you very much Sir! I got the answer.
Commented by mrW1 last updated on 05/Jan/18
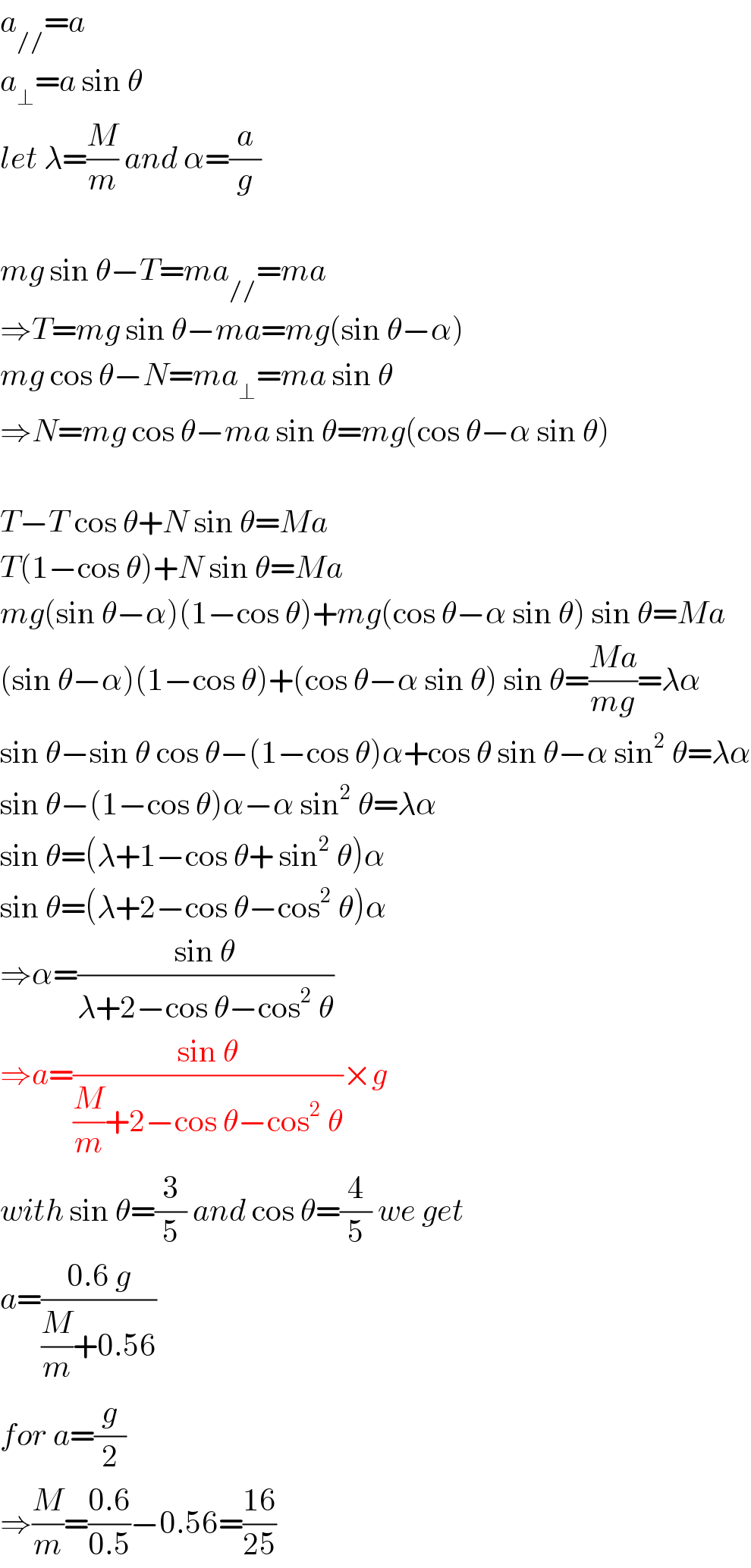
$${a}_{//} ={a} \\ $$$${a}_{\bot} ={a}\:\mathrm{sin}\:\theta \\ $$$${let}\:\lambda=\frac{{M}}{{m}}\:{and}\:\alpha=\frac{{a}}{{g}} \\ $$$$ \\ $$$${mg}\:\mathrm{sin}\:\theta−{T}={ma}_{//} ={ma} \\ $$$$\Rightarrow{T}={mg}\:\mathrm{sin}\:\theta−{ma}={mg}\left(\mathrm{sin}\:\theta−\alpha\right) \\ $$$${mg}\:\mathrm{cos}\:\theta−{N}={ma}_{\bot} ={ma}\:\mathrm{sin}\:\theta \\ $$$$\Rightarrow{N}={mg}\:\mathrm{cos}\:\theta−{ma}\:\mathrm{sin}\:\theta={mg}\left(\mathrm{cos}\:\theta−\alpha\:\mathrm{sin}\:\theta\right) \\ $$$$ \\ $$$${T}−{T}\:\mathrm{cos}\:\theta+{N}\:\mathrm{sin}\:\theta={Ma} \\ $$$${T}\left(\mathrm{1}−\mathrm{cos}\:\theta\right)+{N}\:\mathrm{sin}\:\theta={Ma} \\ $$$${mg}\left(\mathrm{sin}\:\theta−\alpha\right)\left(\mathrm{1}−\mathrm{cos}\:\theta\right)+{mg}\left(\mathrm{cos}\:\theta−\alpha\:\mathrm{sin}\:\theta\right)\:\mathrm{sin}\:\theta={Ma} \\ $$$$\left(\mathrm{sin}\:\theta−\alpha\right)\left(\mathrm{1}−\mathrm{cos}\:\theta\right)+\left(\mathrm{cos}\:\theta−\alpha\:\mathrm{sin}\:\theta\right)\:\mathrm{sin}\:\theta=\frac{{Ma}}{{mg}}=\lambda\alpha \\ $$$$\mathrm{sin}\:\theta−\mathrm{sin}\:\theta\:\mathrm{cos}\:\theta−\left(\mathrm{1}−\mathrm{cos}\:\theta\right)\alpha+\mathrm{cos}\:\theta\:\mathrm{sin}\:\theta−\alpha\:\mathrm{sin}^{\mathrm{2}} \:\theta=\lambda\alpha \\ $$$$\mathrm{sin}\:\theta−\left(\mathrm{1}−\mathrm{cos}\:\theta\right)\alpha−\alpha\:\mathrm{sin}^{\mathrm{2}} \:\theta=\lambda\alpha \\ $$$$\mathrm{sin}\:\theta=\left(\lambda+\mathrm{1}−\mathrm{cos}\:\theta+\:\mathrm{sin}^{\mathrm{2}} \:\theta\right)\alpha \\ $$$$\mathrm{sin}\:\theta=\left(\lambda+\mathrm{2}−\mathrm{cos}\:\theta−\mathrm{cos}^{\mathrm{2}} \:\theta\right)\alpha \\ $$$$\Rightarrow\alpha=\frac{\mathrm{sin}\:\theta}{\lambda+\mathrm{2}−\mathrm{cos}\:\theta−\mathrm{cos}^{\mathrm{2}} \:\theta} \\ $$$$\Rightarrow{a}=\frac{\mathrm{sin}\:\theta}{\frac{{M}}{{m}}+\mathrm{2}−\mathrm{cos}\:\theta−\mathrm{cos}^{\mathrm{2}} \:\theta}×{g} \\ $$$${with}\:\mathrm{sin}\:\theta=\frac{\mathrm{3}}{\mathrm{5}}\:{and}\:\mathrm{cos}\:\theta=\frac{\mathrm{4}}{\mathrm{5}}\:{we}\:{get} \\ $$$${a}=\frac{\mathrm{0}.\mathrm{6}\:{g}}{\frac{{M}}{{m}}+\mathrm{0}.\mathrm{56}} \\ $$$${for}\:{a}=\frac{{g}}{\mathrm{2}} \\ $$$$\Rightarrow\frac{{M}}{{m}}=\frac{\mathrm{0}.\mathrm{6}}{\mathrm{0}.\mathrm{5}}−\mathrm{0}.\mathrm{56}=\frac{\mathrm{16}}{\mathrm{25}} \\ $$
Commented by Tinkutara last updated on 05/Jan/18
I really appreciate this.
