Question Number 27332 by ajfour last updated on 05/Jan/18
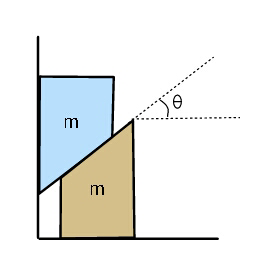
Commented by ajfour last updated on 05/Jan/18

$${Find}\:{acceleration}\:{of}\:{blue}\:{and} \\ $$$${brown}\:{blocks}.\:{Friction}\:{coefficient} \\ $$$${is}\:\boldsymbol{\mu}\:{everywhere}\:\left({sufficiently}\:{less},\right. \\ $$$$\left.{and}\:{permits}\:{motion}\right). \\ $$
Answered by mrW1 last updated on 05/Jan/18
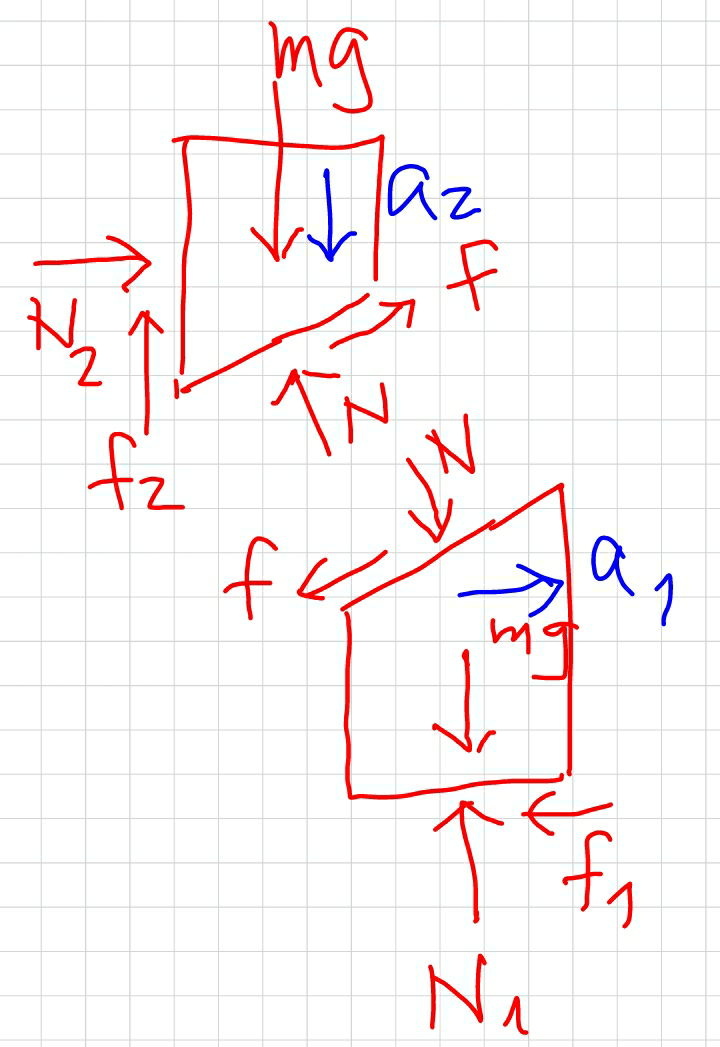
Commented by mrW1 last updated on 05/Jan/18
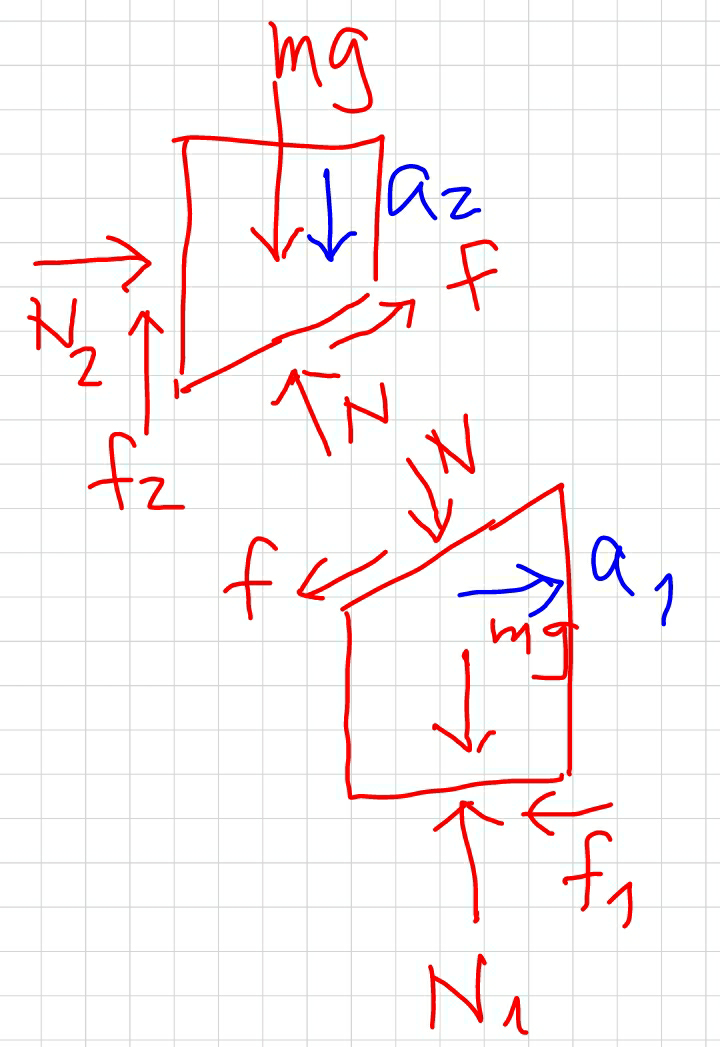
Commented by mrW1 last updated on 06/Jan/18
![(a_2 /a_1 )=tan θ N_2 =N sin θ−f cos θ=N(sin θ−μ cos θ) mg−f_2 −N cos θ−f sin θ=ma_2 mg−μN_2 −N (cos θ+μ sin θ)=ma_2 mg−μN(sin θ−μ cos θ)−N (cos θ+μ sin θ)=ma_2 mg−N(2μsin θ−μ^2 cos θ+cos θ)=ma_2 N_1 =mg+N cos θ+f sin θ=mg+N(cos θ+μ sin θ) N sin θ−f cos θ−f_1 =ma_1 N(sin θ−μ cos θ)−μN_1 =ma_1 N(sin θ−μ cos θ)−μmg−μN(cos θ+μ sin θ)=ma_1 N(sin θ−μ^2 sin θ−2μ cos θ)−μmg=ma_1 ((mg−N(2μsin θ−μ^2 cos θ+cos θ))/(N(sin θ−μ^2 sin θ−2μ cos θ)−μmg))=((ma_2 )/(ma_1 ))=tan θ=((sin θ)/(cos θ)) mg cos θ−N(2μsin θ cos θ−μ^2 cos^2 θ+cos^2 θ)=N(sin^2 θ−μ^2 sin^2 θ−2μ sin θ cos θ)−μmg sin θ N(2μsin θ cos θ−μ^2 cos^2 θ+cos^2 θ+sin^2 θ−μ^2 sin^2 θ−2μ sin θ cos θ)=mg(cos θ+μsin θ) N(1−μ^2 )=mg(cos θ+μsin θ) ⇒N=(((cos θ+μ sin θ)mg)/(1−μ^2 )) a_1 =((N(sin θ−μ^2 sin θ−2μ cos θ))/m)−μg a_1 =(((cos θ+μ sin θ)(sin θ−μ^2 sin θ−2μ cos θ)g)/(1−μ^2 ))−μg ⇒a_1 =[(cos θ+μ sin θ)(sin θ−((2μ)/(1−μ^2 )) cos θ)−μ]g a_2 =g−((N(2μ sin θ+cos θ−μ^2 cos θ))/m) a_2 =g−(((cos θ+μ sin θ)(2μ sin θ+cos θ−μ^2 cos θ)g)/(1−μ^2 )) ⇒a_2 =[1−(cos θ+μ sin θ)(((2μ)/(1−μ^2 )) sin θ+cos θ)]g](https://www.tinkutara.com/question/Q27347.png)
$$\frac{{a}_{\mathrm{2}} }{{a}_{\mathrm{1}} }=\mathrm{tan}\:\theta \\ $$$${N}_{\mathrm{2}} ={N}\:\mathrm{sin}\:\theta−{f}\:\mathrm{cos}\:\theta={N}\left(\mathrm{sin}\:\theta−\mu\:\mathrm{cos}\:\theta\right) \\ $$$${mg}−{f}_{\mathrm{2}} −{N}\:\mathrm{cos}\:\theta−{f}\:\mathrm{sin}\:\theta={ma}_{\mathrm{2}} \\ $$$${mg}−\mu{N}_{\mathrm{2}} −{N}\:\left(\mathrm{cos}\:\theta+\mu\:\mathrm{sin}\:\theta\right)={ma}_{\mathrm{2}} \\ $$$${mg}−\mu{N}\left(\mathrm{sin}\:\theta−\mu\:\mathrm{cos}\:\theta\right)−{N}\:\left(\mathrm{cos}\:\theta+\mu\:\mathrm{sin}\:\theta\right)={ma}_{\mathrm{2}} \\ $$$${mg}−{N}\left(\mathrm{2}\mu\mathrm{sin}\:\theta−\mu^{\mathrm{2}} \:\mathrm{cos}\:\theta+\mathrm{cos}\:\theta\right)={ma}_{\mathrm{2}} \\ $$$$ \\ $$$${N}_{\mathrm{1}} ={mg}+{N}\:\mathrm{cos}\:\theta+{f}\:\mathrm{sin}\:\theta={mg}+{N}\left(\mathrm{cos}\:\theta+\mu\:\mathrm{sin}\:\theta\right) \\ $$$${N}\:\mathrm{sin}\:\theta−{f}\:\mathrm{cos}\:\theta−{f}_{\mathrm{1}} ={ma}_{\mathrm{1}} \\ $$$${N}\left(\mathrm{sin}\:\theta−\mu\:\mathrm{cos}\:\theta\right)−\mu{N}_{\mathrm{1}} ={ma}_{\mathrm{1}} \\ $$$${N}\left(\mathrm{sin}\:\theta−\mu\:\mathrm{cos}\:\theta\right)−\mu{mg}−\mu{N}\left(\mathrm{cos}\:\theta+\mu\:\mathrm{sin}\:\theta\right)={ma}_{\mathrm{1}} \\ $$$${N}\left(\mathrm{sin}\:\theta−\mu^{\mathrm{2}} \:\mathrm{sin}\:\theta−\mathrm{2}\mu\:\mathrm{cos}\:\theta\right)−\mu{mg}={ma}_{\mathrm{1}} \\ $$$$ \\ $$$$\frac{{mg}−{N}\left(\mathrm{2}\mu\mathrm{sin}\:\theta−\mu^{\mathrm{2}} \:\mathrm{cos}\:\theta+\mathrm{cos}\:\theta\right)}{{N}\left(\mathrm{sin}\:\theta−\mu^{\mathrm{2}} \:\mathrm{sin}\:\theta−\mathrm{2}\mu\:\mathrm{cos}\:\theta\right)−\mu{mg}}=\frac{{ma}_{\mathrm{2}} }{{ma}_{\mathrm{1}} }=\mathrm{tan}\:\theta=\frac{\mathrm{sin}\:\theta}{\mathrm{cos}\:\theta} \\ $$$${mg}\:\mathrm{cos}\:\theta−{N}\left(\mathrm{2}\mu\mathrm{sin}\:\theta\:\mathrm{cos}\:\theta−\mu^{\mathrm{2}} \:\mathrm{cos}^{\mathrm{2}} \:\theta+\mathrm{cos}^{\mathrm{2}} \:\theta\right)={N}\left(\mathrm{sin}^{\mathrm{2}} \:\theta−\mu^{\mathrm{2}} \:\mathrm{sin}^{\mathrm{2}} \:\theta−\mathrm{2}\mu\:\mathrm{sin}\:\theta\:\mathrm{cos}\:\theta\right)−\mu{mg}\:\mathrm{sin}\:\theta \\ $$$${N}\left(\mathrm{2}\mu\mathrm{sin}\:\theta\:\mathrm{cos}\:\theta−\mu^{\mathrm{2}} \:\mathrm{cos}^{\mathrm{2}} \:\theta+\mathrm{cos}^{\mathrm{2}} \:\theta+\mathrm{sin}^{\mathrm{2}} \:\theta−\mu^{\mathrm{2}} \:\mathrm{sin}^{\mathrm{2}} \:\theta−\mathrm{2}\mu\:\mathrm{sin}\:\theta\:\mathrm{cos}\:\theta\right)={mg}\left(\mathrm{cos}\:\theta+\mu\mathrm{sin}\:\theta\right) \\ $$$${N}\left(\mathrm{1}−\mu^{\mathrm{2}} \right)={mg}\left(\mathrm{cos}\:\theta+\mu\mathrm{sin}\:\theta\right) \\ $$$$\Rightarrow{N}=\frac{\left(\mathrm{cos}\:\theta+\mu\:\mathrm{sin}\:\theta\right){mg}}{\mathrm{1}−\mu^{\mathrm{2}} } \\ $$$$ \\ $$$${a}_{\mathrm{1}} =\frac{{N}\left(\mathrm{sin}\:\theta−\mu^{\mathrm{2}} \:\mathrm{sin}\:\theta−\mathrm{2}\mu\:\mathrm{cos}\:\theta\right)}{{m}}−\mu{g} \\ $$$${a}_{\mathrm{1}} =\frac{\left(\mathrm{cos}\:\theta+\mu\:\mathrm{sin}\:\theta\right)\left(\mathrm{sin}\:\theta−\mu^{\mathrm{2}} \:\mathrm{sin}\:\theta−\mathrm{2}\mu\:\mathrm{cos}\:\theta\right){g}}{\mathrm{1}−\mu^{\mathrm{2}} }−\mu{g} \\ $$$$\Rightarrow{a}_{\mathrm{1}} =\left[\left(\mathrm{cos}\:\theta+\mu\:\mathrm{sin}\:\theta\right)\left(\mathrm{sin}\:\theta−\frac{\mathrm{2}\mu}{\mathrm{1}−\mu^{\mathrm{2}} }\:\mathrm{cos}\:\theta\right)−\mu\right]{g} \\ $$$$ \\ $$$${a}_{\mathrm{2}} ={g}−\frac{{N}\left(\mathrm{2}\mu\:\mathrm{sin}\:\theta+\mathrm{cos}\:\theta−\mu^{\mathrm{2}} \:\mathrm{cos}\:\theta\right)}{{m}} \\ $$$${a}_{\mathrm{2}} ={g}−\frac{\left(\mathrm{cos}\:\theta+\mu\:\mathrm{sin}\:\theta\right)\left(\mathrm{2}\mu\:\mathrm{sin}\:\theta+\mathrm{cos}\:\theta−\mu^{\mathrm{2}} \:\mathrm{cos}\:\theta\right){g}}{\mathrm{1}−\mu^{\mathrm{2}} } \\ $$$$\Rightarrow{a}_{\mathrm{2}} =\left[\mathrm{1}−\left(\mathrm{cos}\:\theta+\mu\:\mathrm{sin}\:\theta\right)\left(\frac{\mathrm{2}\mu}{\mathrm{1}−\mu^{\mathrm{2}} }\:\mathrm{sin}\:\theta+\mathrm{cos}\:\theta\right)\right]{g} \\ $$
Commented by ajfour last updated on 05/Jan/18
$${Excellently}\:{presented}\:{and} \\ $$$${handled}\:{Sir}! \\ $$
Commented by mrW1 last updated on 06/Jan/18
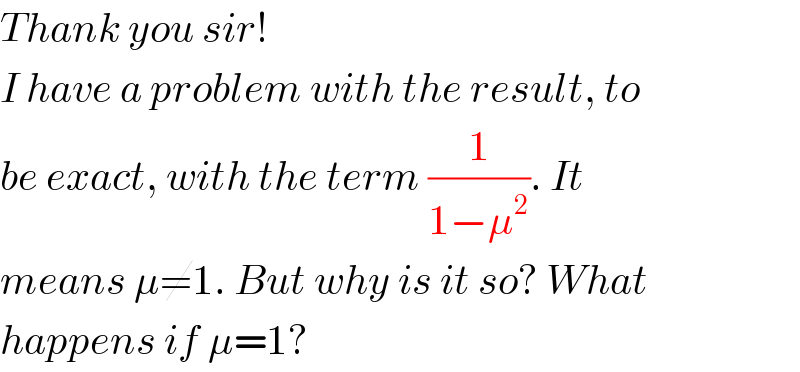
$${Thank}\:{you}\:{sir}! \\ $$$${I}\:{have}\:{a}\:{problem}\:{with}\:{the}\:{result},\:{to} \\ $$$${be}\:{exact},\:{with}\:{the}\:{term}\:\frac{\mathrm{1}}{\mathrm{1}−\mu^{\mathrm{2}} }.\:{It} \\ $$$${means}\:\mu\neq\mathrm{1}.\:{But}\:{why}\:{is}\:{it}\:{so}?\:{What} \\ $$$${happens}\:{if}\:\mu=\mathrm{1}? \\ $$
