Question Number 27446 by amit96 last updated on 07/Jan/18
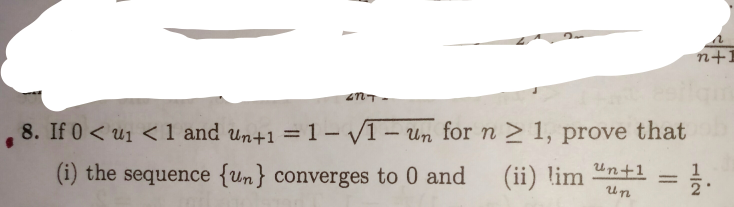
Commented by prakash jain last updated on 08/Jan/18
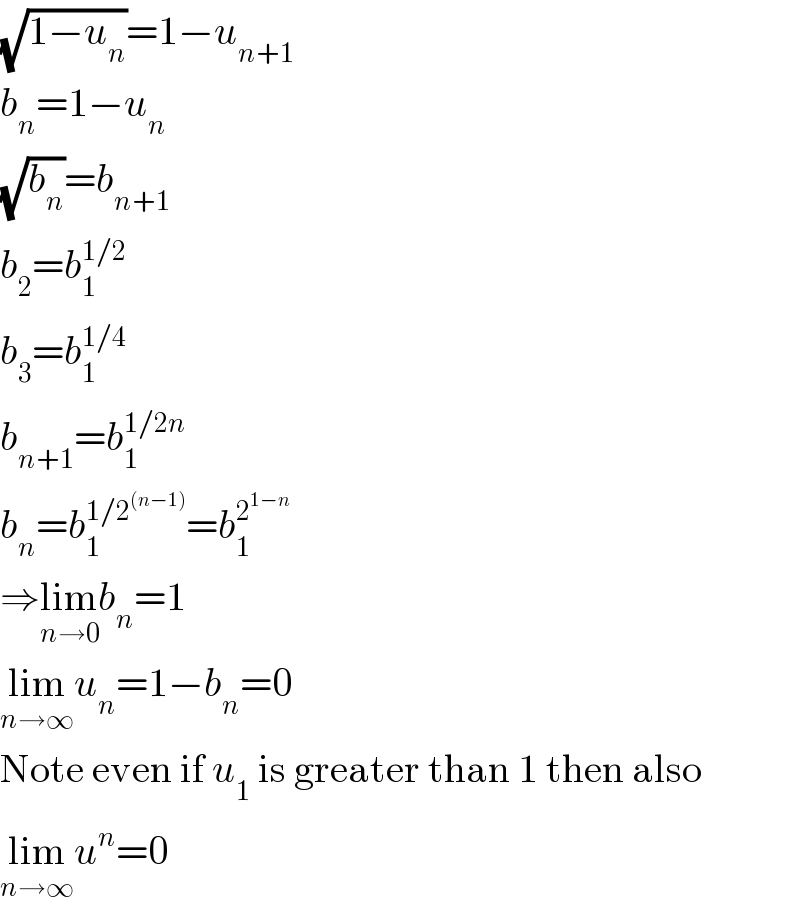
$$\sqrt{\mathrm{1}−{u}_{{n}} }=\mathrm{1}−{u}_{{n}+\mathrm{1}} \\ $$$${b}_{{n}} =\mathrm{1}−{u}_{{n}} \\ $$$$\sqrt{{b}_{{n}} }={b}_{{n}+\mathrm{1}} \\ $$$${b}_{\mathrm{2}} ={b}_{\mathrm{1}} ^{\mathrm{1}/\mathrm{2}} \\ $$$${b}_{\mathrm{3}} ={b}_{\mathrm{1}} ^{\mathrm{1}/\mathrm{4}} \\ $$$${b}_{{n}+\mathrm{1}} ={b}_{\mathrm{1}} ^{\mathrm{1}/\mathrm{2}{n}} \\ $$$${b}_{{n}} ={b}_{\mathrm{1}} ^{\mathrm{1}/\mathrm{2}^{\left({n}−\mathrm{1}\right)} } ={b}_{\mathrm{1}} ^{\mathrm{2}^{\mathrm{1}−{n}} } \\ $$$$\Rightarrow\underset{{n}\rightarrow\mathrm{0}} {\mathrm{lim}}{b}_{{n}} =\mathrm{1} \\ $$$$\underset{{n}\rightarrow\infty} {\mathrm{lim}}{u}_{{n}} =\mathrm{1}−{b}_{{n}} =\mathrm{0} \\ $$$$\mathrm{Note}\:\mathrm{even}\:\mathrm{if}\:{u}_{\mathrm{1}} \:\mathrm{is}\:\mathrm{greater}\:\mathrm{than}\:\mathrm{1}\:\mathrm{then}\:\mathrm{also} \\ $$$$\underset{{n}\rightarrow\infty} {\mathrm{lim}}{u}^{{n}} =\mathrm{0} \\ $$
Commented by prakash jain last updated on 08/Jan/18
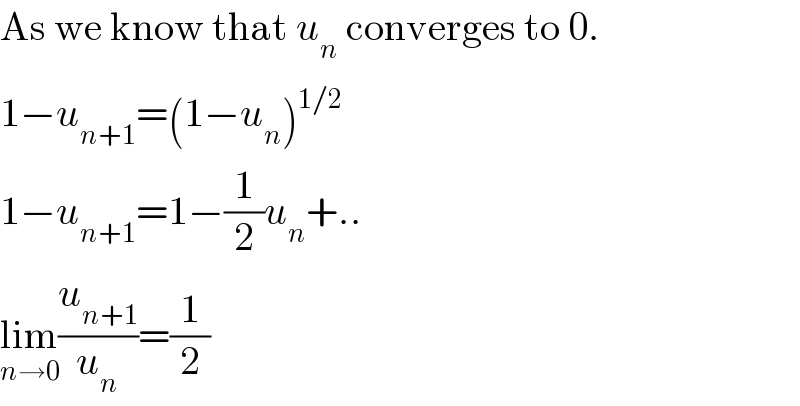
$$\mathrm{As}\:\mathrm{we}\:\mathrm{know}\:\mathrm{that}\:{u}_{{n}} \:\mathrm{converges}\:\mathrm{to}\:\mathrm{0}. \\ $$$$\mathrm{1}−{u}_{{n}+\mathrm{1}} =\left(\mathrm{1}−{u}_{{n}} \right)^{\mathrm{1}/\mathrm{2}} \\ $$$$\mathrm{1}−{u}_{{n}+\mathrm{1}} =\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}{u}_{{n}} +.. \\ $$$$\underset{{n}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{{u}_{{n}+\mathrm{1}} }{{u}_{{n}} }=\frac{\mathrm{1}}{\mathrm{2}} \\ $$
Commented by amit96 last updated on 31/Jan/18

$${thanks} \\ $$$$ \\ $$
