Question Number 27469 by byaw last updated on 07/Jan/18

Commented by byaw last updated on 31/Jan/18
please help solve this problem
thank you
Commented by Tinkutara last updated on 31/Jan/18
Is the answer 399?
Commented by byaw last updated on 04/Feb/18

$${Yes} \\ $$
Answered by Tinkutara last updated on 31/Jan/18
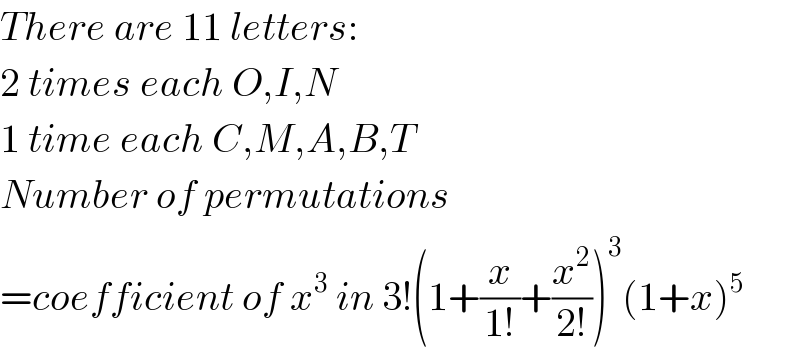
$${There}\:{are}\:\mathrm{11}\:{letters}: \\ $$$$\mathrm{2}\:{times}\:{each}\:{O},{I},{N} \\ $$$$\mathrm{1}\:{time}\:{each}\:{C},{M},{A},{B},{T} \\ $$$${Number}\:{of}\:{permutations} \\ $$$$={coefficient}\:{of}\:{x}^{\mathrm{3}} \:{in}\:\mathrm{3}!\left(\mathrm{1}+\frac{{x}}{\mathrm{1}!}+\frac{{x}^{\mathrm{2}} }{\mathrm{2}!}\right)^{\mathrm{3}} \left(\mathrm{1}+{x}\right)^{\mathrm{5}} \\ $$
Commented by byaw last updated on 04/Feb/18

$${thank}\:{you}\:{for}\:{the}\:{work}. \\ $$$${Can}\:{you}\:{please}\:{explain}\:{the}\:{formula}\:{for}\:{me}? \\ $$$${In}\:{case}\:{I}\:{get}\:{similar}\:{question} \\ $$$${how}\:{can}\:{i}\:{apply}\:{the}\:{formula}? \\ $$$$ \\ $$$${How}\:{can}\:{I}\:{use}\:{the}\:{formula}\:{to}\:{solve}\:{the}\:{problem}\:{blow}? \\ $$$$\mathrm{How}\:\mathrm{many}\:\mathrm{arrangements}\:\mathrm{are}\:\mathrm{there}\:\mathrm{in}\:\mathrm{the} \\ $$$$\mathrm{word}\:\mathrm{COMMUNICATION}\:\mathrm{taken} \\ $$$$\mathrm{4}\:\mathrm{letters}\:{at}\:{a}\:{time}. \\ $$$${Thank}\:{you}. \\ $$
