Menu Close

Question-27539

Tinku Tara 0 Comments
Pin




Question Number 27539 by Mr eaay last updated on 08/Jan/18
Commented by Tinkutara last updated on 08/Jan/18
For second part see question 27445 and 27400.
Answered by Joel578 last updated on 09/Jan/18
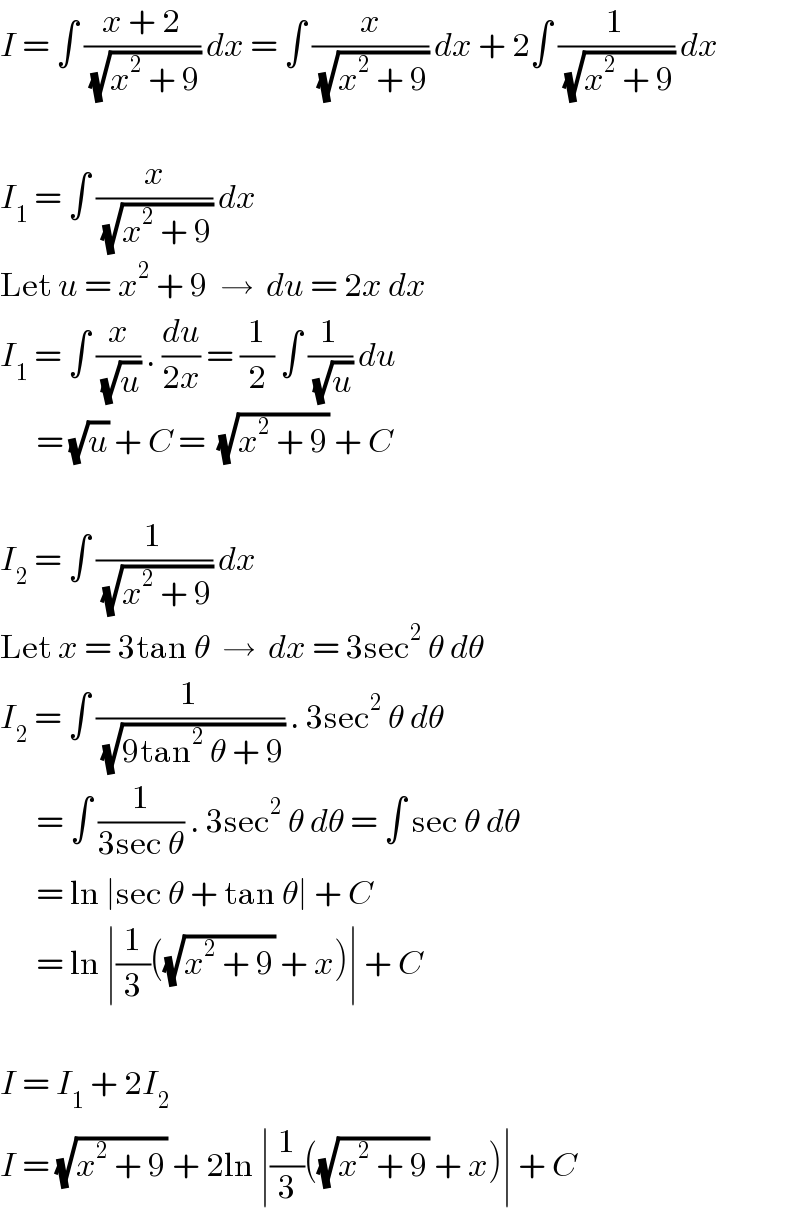
I = ∫ ((x + 2)/( (√(x^2 + 9)))) dx = ∫ (x/( (√(x^2 + 9)))) dx + 2∫ (1/( (√(x^2 + 9)))) dx I_1 = ∫ (x/( (√(x^2 + 9)))) dx Let u = x^2 + 9 → du = 2x dx I_1 = ∫ (x/( (√u))) . (du/(2x)) = (1/2) ∫ (1/( (√u))) du = (√u) + C = (√(x^2 + 9)) + C I_2 = ∫ (1/( (√(x^2 + 9)))) dx Let x = 3tan θ → dx = 3sec^2 θ dθ I_2 = ∫ (1/( (√(9tan^2 θ + 9)))) . 3sec^2 θ dθ = ∫ (1/(3sec θ)) . 3sec^2 θ dθ = ∫ sec θ dθ = ln ∣sec θ + tan θ∣ + C = ln ∣(1/3)((√(x^2 + 9)) + x)∣ + C I = I_1 + 2I_2 I = (√(x^2 + 9)) + 2ln ∣(1/3)((√(x^2 + 9)) + x)∣ + C
$${I}\:=\:\int\:\frac{{x}\:+\:\mathrm{2}}{\:\sqrt{{x}^{\mathrm{2}} \:+\:\mathrm{9}}}\:{dx}\:=\:\int\:\frac{{x}}{\:\sqrt{{x}^{\mathrm{2}} \:+\:\mathrm{9}}}\:{dx}\:+\:\mathrm{2}\int\:\frac{\mathrm{1}}{\:\sqrt{{x}^{\mathrm{2}} \:+\:\mathrm{9}}}\:{dx} \\ $$$$ \\ $$$${I}_{\mathrm{1}} \:=\:\int\:\frac{{x}}{\:\sqrt{{x}^{\mathrm{2}} \:+\:\mathrm{9}}}\:{dx} \\ $$$$\mathrm{Let}\:{u}\:=\:{x}^{\mathrm{2}} \:+\:\mathrm{9}\:\:\rightarrow\:\:{du}\:=\:\mathrm{2}{x}\:{dx} \\ $$$${I}_{\mathrm{1}} \:=\:\int\:\frac{{x}}{\:\sqrt{{u}}}\:.\:\frac{{du}}{\mathrm{2}{x}}\:=\:\frac{\mathrm{1}}{\mathrm{2}}\:\int\:\frac{\mathrm{1}}{\:\sqrt{{u}}}\:{du} \\ $$$$\:\:\:\:\:\:=\:\sqrt{{u}}\:+\:{C}\:=\:\:\sqrt{{x}^{\mathrm{2}} \:+\:\mathrm{9}}\:+\:{C} \\ $$$$ \\ $$$${I}_{\mathrm{2}} \:=\:\int\:\frac{\mathrm{1}}{\:\sqrt{{x}^{\mathrm{2}} \:+\:\mathrm{9}}}\:{dx} \\ $$$$\mathrm{Let}\:{x}\:=\:\mathrm{3tan}\:\theta\:\:\rightarrow\:\:{dx}\:=\:\mathrm{3sec}^{\mathrm{2}} \:\theta\:{d}\theta \\ $$$${I}_{\mathrm{2}} \:=\:\int\:\frac{\mathrm{1}}{\:\sqrt{\mathrm{9tan}^{\mathrm{2}} \:\theta\:+\:\mathrm{9}}}\:.\:\mathrm{3sec}^{\mathrm{2}} \:\theta\:{d}\theta \\ $$$$\:\:\:\:\:\:=\:\int\:\frac{\mathrm{1}}{\mathrm{3sec}\:\theta}\:.\:\mathrm{3sec}^{\mathrm{2}} \:\theta\:{d}\theta\:=\:\int\:\mathrm{sec}\:\theta\:{d}\theta \\ $$$$\:\:\:\:\:\:=\:\mathrm{ln}\:\mid\mathrm{sec}\:\theta\:+\:\mathrm{tan}\:\theta\mid\:+\:{C} \\ $$$$\:\:\:\:\:\:=\:\mathrm{ln}\:\mid\frac{\mathrm{1}}{\mathrm{3}}\left(\sqrt{{x}^{\mathrm{2}} \:+\:\mathrm{9}}\:+\:{x}\right)\mid\:+\:{C} \\ $$$$ \\ $$$${I}\:=\:{I}_{\mathrm{1}} \:+\:\mathrm{2}{I}_{\mathrm{2}} \\ $$$${I}\:=\:\sqrt{{x}^{\mathrm{2}} \:+\:\mathrm{9}}\:+\:\mathrm{2ln}\:\mid\frac{\mathrm{1}}{\mathrm{3}}\left(\sqrt{{x}^{\mathrm{2}} \:+\:\mathrm{9}}\:+\:{x}\right)\mid\:+\:{C} \\ $$
Answered by Joel578 last updated on 09/Jan/18
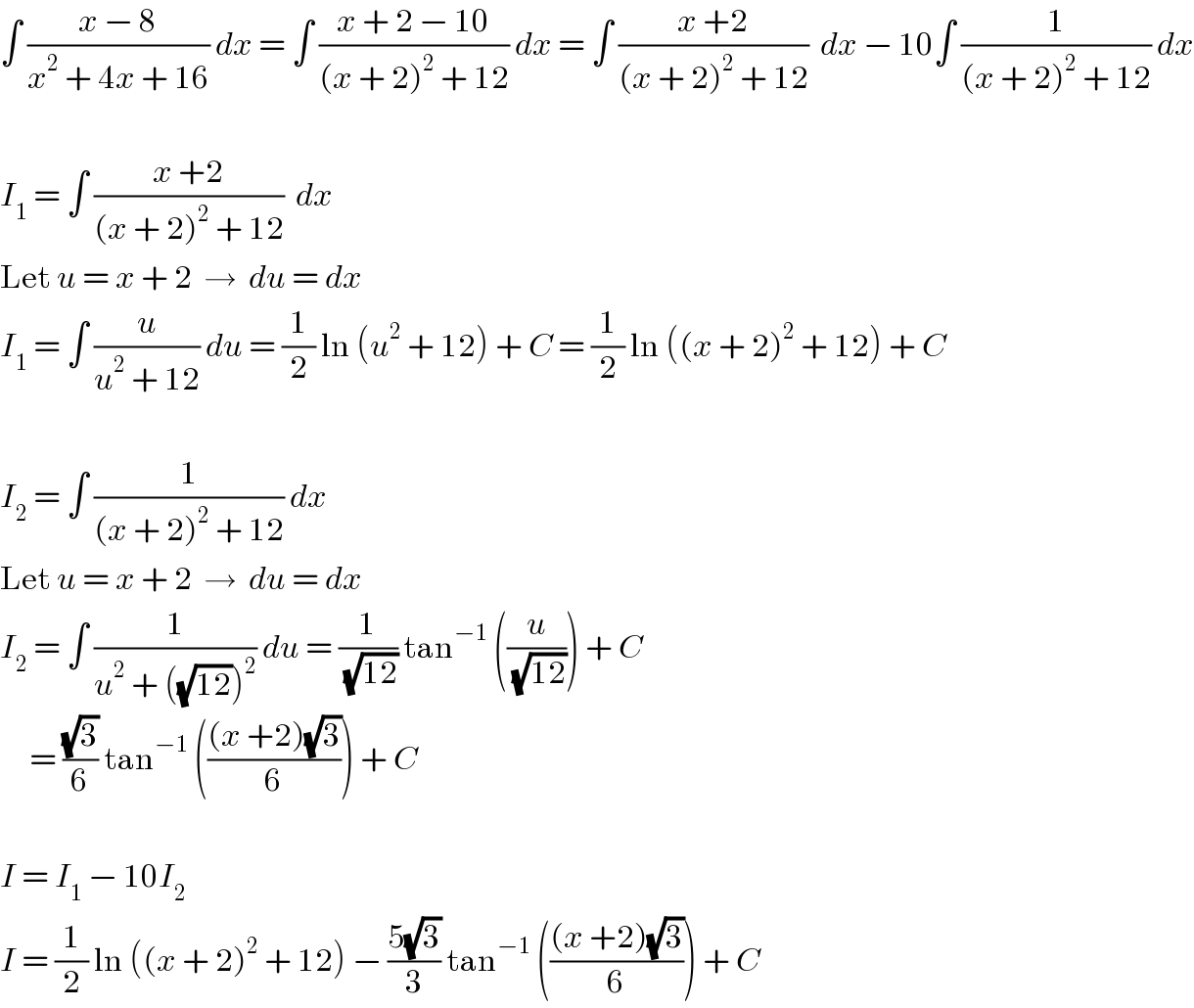
∫ ((x − 8)/(x^2 + 4x + 16)) dx = ∫ ((x + 2 − 10)/((x + 2)^2 + 12)) dx = ∫ ((x +2)/((x + 2)^2 + 12)) dx − 10∫ (1/((x + 2)^2 + 12)) dx I_1 = ∫ ((x +2)/((x + 2)^2 + 12)) dx Let u = x + 2 → du = dx I_1 = ∫ (u/(u^2 + 12)) du = (1/2) ln (u^2 + 12) + C = (1/2) ln ((x + 2)^2 + 12) + C I_2 = ∫ (1/((x + 2)^2 + 12)) dx Let u = x + 2 → du = dx I_2 = ∫ (1/(u^2 + ((√(12)))^2 )) du = (1/( (√(12)))) tan^(−1) ((u/( (√(12))))) + C = ((√3)/6) tan^(−1) ((((x +2)(√3))/6)) + C I = I_1 − 10I_2 I = (1/2) ln ((x + 2)^2 + 12) − ((5(√3))/3) tan^(−1) ((((x +2)(√3))/6)) + C
$$\int\:\frac{{x}\:−\:\mathrm{8}}{{x}^{\mathrm{2}} \:+\:\mathrm{4}{x}\:+\:\mathrm{16}}\:{dx}\:=\:\int\:\frac{{x}\:+\:\mathrm{2}\:−\:\mathrm{10}}{\left({x}\:+\:\mathrm{2}\right)^{\mathrm{2}} \:+\:\mathrm{12}}\:{dx}\:=\:\int\:\frac{{x}\:+\mathrm{2}}{\left({x}\:+\:\mathrm{2}\right)^{\mathrm{2}} \:+\:\mathrm{12}}\:\:{dx}\:−\:\mathrm{10}\int\:\frac{\mathrm{1}}{\left({x}\:+\:\mathrm{2}\right)^{\mathrm{2}} \:+\:\mathrm{12}}\:{dx} \\ $$$$ \\ $$$${I}_{\mathrm{1}} \:=\:\int\:\frac{{x}\:+\mathrm{2}}{\left({x}\:+\:\mathrm{2}\right)^{\mathrm{2}} \:+\:\mathrm{12}}\:\:{dx} \\ $$$$\mathrm{Let}\:{u}\:=\:{x}\:+\:\mathrm{2}\:\:\rightarrow\:\:{du}\:=\:{dx} \\ $$$${I}_{\mathrm{1}} \:=\:\int\:\frac{{u}}{{u}^{\mathrm{2}} \:+\:\mathrm{12}}\:{du}\:=\:\frac{\mathrm{1}}{\mathrm{2}}\:\mathrm{ln}\:\left({u}^{\mathrm{2}} \:+\:\mathrm{12}\right)\:+\:{C}\:=\:\frac{\mathrm{1}}{\mathrm{2}}\:\mathrm{ln}\:\left(\left({x}\:+\:\mathrm{2}\right)^{\mathrm{2}} \:+\:\mathrm{12}\right)\:+\:{C} \\ $$$$ \\ $$$${I}_{\mathrm{2}} \:=\:\int\:\frac{\mathrm{1}}{\left({x}\:+\:\mathrm{2}\right)^{\mathrm{2}} \:+\:\mathrm{12}}\:{dx} \\ $$$$\mathrm{Let}\:{u}\:=\:{x}\:+\:\mathrm{2}\:\:\rightarrow\:\:{du}\:=\:{dx} \\ $$$${I}_{\mathrm{2}} \:=\:\int\:\frac{\mathrm{1}}{{u}^{\mathrm{2}} \:+\:\left(\sqrt{\mathrm{12}}\right)^{\mathrm{2}} }\:{du}\:=\:\frac{\mathrm{1}}{\:\sqrt{\mathrm{12}}}\:\mathrm{tan}^{−\mathrm{1}} \:\left(\frac{{u}}{\:\sqrt{\mathrm{12}}}\right)\:+\:{C} \\ $$$$\:\:\:\:\:=\:\frac{\sqrt{\mathrm{3}}}{\mathrm{6}}\:\mathrm{tan}^{−\mathrm{1}} \:\left(\frac{\left({x}\:+\mathrm{2}\right)\sqrt{\mathrm{3}}}{\mathrm{6}}\right)\:+\:{C} \\ $$$$ \\ $$$${I}\:=\:{I}_{\mathrm{1}} \:−\:\mathrm{10}{I}_{\mathrm{2}} \\ $$$${I}\:=\:\frac{\mathrm{1}}{\mathrm{2}}\:\mathrm{ln}\:\left(\left({x}\:+\:\mathrm{2}\right)^{\mathrm{2}} \:+\:\mathrm{12}\right)\:−\:\frac{\mathrm{5}\sqrt{\mathrm{3}}}{\mathrm{3}}\:\mathrm{tan}^{−\mathrm{1}} \:\left(\frac{\left({x}\:+\mathrm{2}\right)\sqrt{\mathrm{3}}}{\mathrm{6}}\right)\:+\:{C} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *