Question Number 27564 by Tinkutara last updated on 09/Jan/18

Commented by Tinkutara last updated on 09/Jan/18
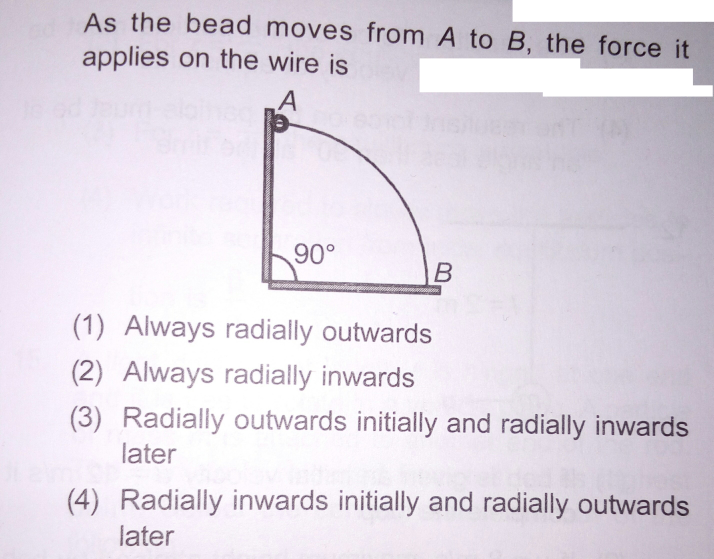
Commented by mrW2 last updated on 12/Jan/18
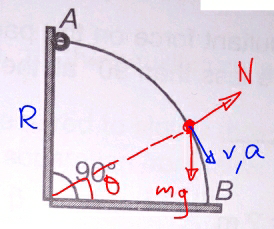
Commented by mrW2 last updated on 12/Jan/18
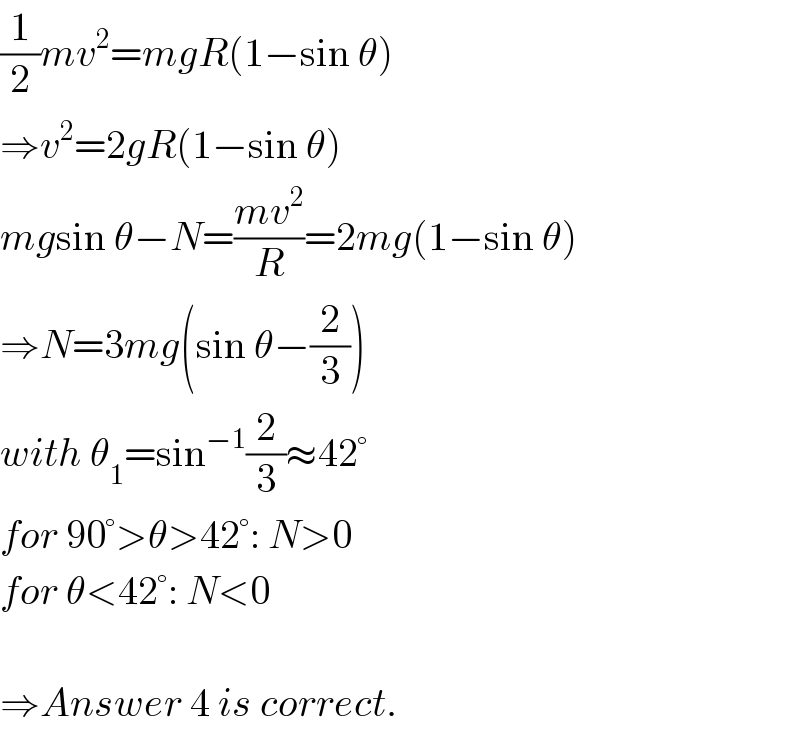
$$\frac{\mathrm{1}}{\mathrm{2}}{mv}^{\mathrm{2}} ={mgR}\left(\mathrm{1}−\mathrm{sin}\:\theta\right) \\ $$$$\Rightarrow{v}^{\mathrm{2}} =\mathrm{2}{gR}\left(\mathrm{1}−\mathrm{sin}\:\theta\right) \\ $$$${mg}\mathrm{sin}\:\theta−{N}=\frac{{mv}^{\mathrm{2}} }{{R}}=\mathrm{2}{mg}\left(\mathrm{1}−\mathrm{sin}\:\theta\right) \\ $$$$\Rightarrow{N}=\mathrm{3}{mg}\left(\mathrm{sin}\:\theta−\frac{\mathrm{2}}{\mathrm{3}}\right) \\ $$$${with}\:\theta_{\mathrm{1}} =\mathrm{sin}^{−\mathrm{1}} \frac{\mathrm{2}}{\mathrm{3}}\approx\mathrm{42}° \\ $$$${for}\:\mathrm{90}°>\theta>\mathrm{42}°:\:{N}>\mathrm{0} \\ $$$${for}\:\theta<\mathrm{42}°:\:{N}<\mathrm{0} \\ $$$$ \\ $$$$\Rightarrow{Answer}\:\mathrm{4}\:{is}\:{correct}. \\ $$
Commented by Tinkutara last updated on 12/Jan/18
Thank you very much Sir! I got the answer.
