Question Number 27640 by Tinkutara last updated on 11/Jan/18

Answered by ajfour last updated on 11/Jan/18
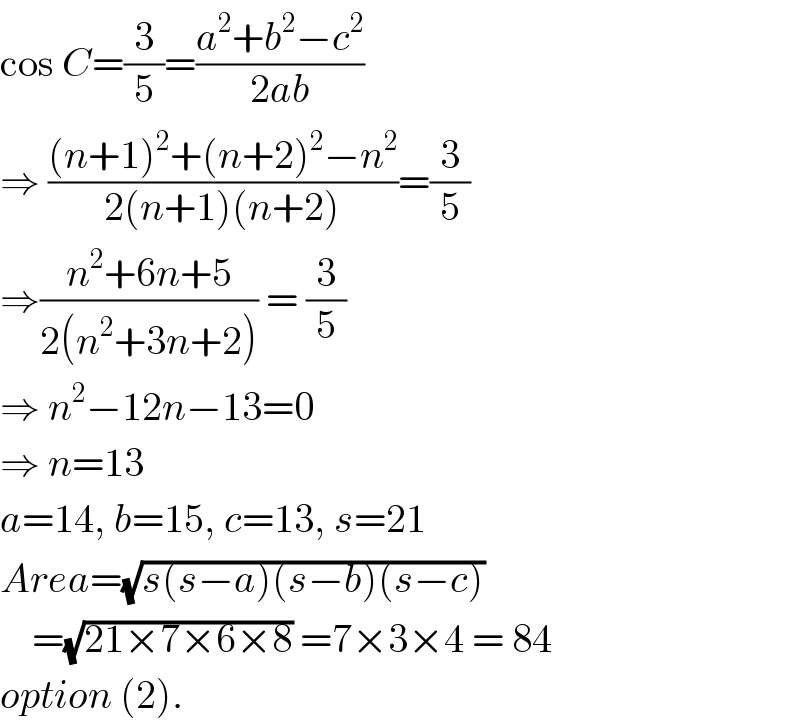
$$\mathrm{cos}\:{C}=\frac{\mathrm{3}}{\mathrm{5}}=\frac{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} −{c}^{\mathrm{2}} }{\mathrm{2}{ab}} \\ $$$$\Rightarrow\:\frac{\left({n}+\mathrm{1}\right)^{\mathrm{2}} +\left({n}+\mathrm{2}\right)^{\mathrm{2}} −{n}^{\mathrm{2}} }{\mathrm{2}\left({n}+\mathrm{1}\right)\left({n}+\mathrm{2}\right)}=\frac{\mathrm{3}}{\mathrm{5}} \\ $$$$\Rightarrow\frac{{n}^{\mathrm{2}} +\mathrm{6}{n}+\mathrm{5}}{\mathrm{2}\left({n}^{\mathrm{2}} +\mathrm{3}{n}+\mathrm{2}\right)}\:=\:\frac{\mathrm{3}}{\mathrm{5}} \\ $$$$\Rightarrow\:{n}^{\mathrm{2}} −\mathrm{12}{n}−\mathrm{13}=\mathrm{0} \\ $$$$\Rightarrow\:{n}=\mathrm{13} \\ $$$${a}=\mathrm{14},\:{b}=\mathrm{15},\:{c}=\mathrm{13},\:{s}=\mathrm{21} \\ $$$${Area}=\sqrt{{s}\left({s}−{a}\right)\left({s}−{b}\right)\left({s}−{c}\right)} \\ $$$$\:\:\:\:=\sqrt{\mathrm{21}×\mathrm{7}×\mathrm{6}×\mathrm{8}}\:=\mathrm{7}×\mathrm{3}×\mathrm{4}\:=\:\mathrm{84} \\ $$$${option}\:\left(\mathrm{2}\right). \\ $$
Commented by Tinkutara last updated on 12/Jan/18
Thank you very much Sir! I got the answer.
