Question Number 27850 by v7277668420 last updated on 15/Jan/18
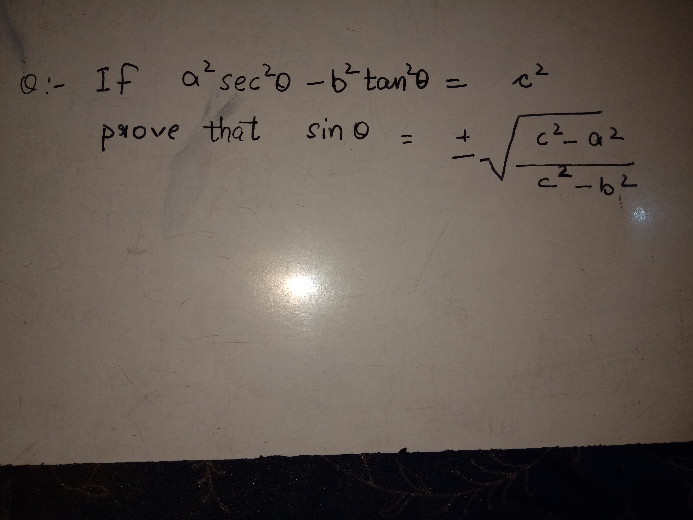
Answered by bmind4860 last updated on 15/Jan/18
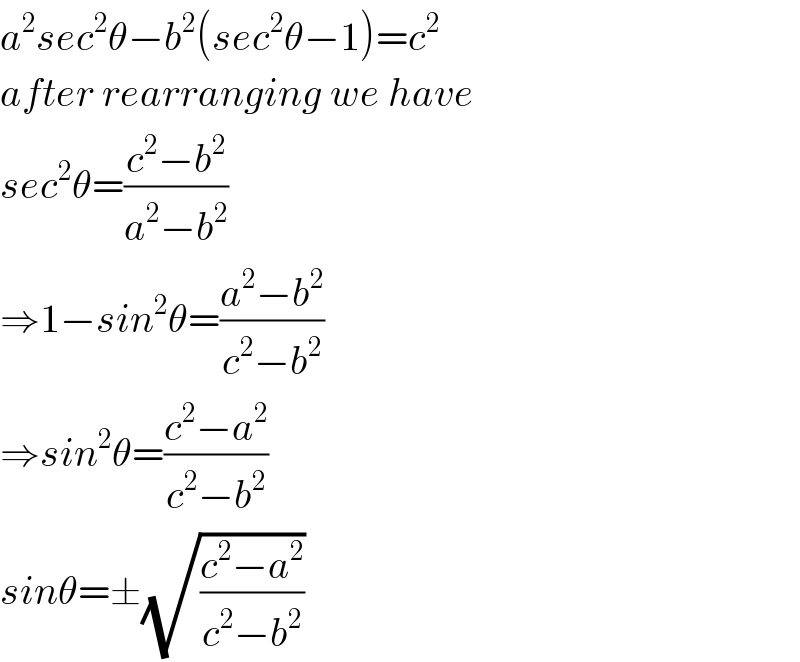
$${a}^{\mathrm{2}} {sec}^{\mathrm{2}} \theta−{b}^{\mathrm{2}} \left({sec}^{\mathrm{2}} \theta−\mathrm{1}\right)={c}^{\mathrm{2}} \\ $$$${after}\:{rearranging}\:{we}\:{have} \\ $$$${sec}^{\mathrm{2}} \theta=\frac{{c}^{\mathrm{2}} −{b}^{\mathrm{2}} }{{a}^{\mathrm{2}} −{b}^{\mathrm{2}} } \\ $$$$\Rightarrow\mathrm{1}−{sin}^{\mathrm{2}} \theta=\frac{{a}^{\mathrm{2}} −{b}^{\mathrm{2}} }{{c}^{\mathrm{2}} −{b}^{\mathrm{2}} } \\ $$$$\Rightarrow{sin}^{\mathrm{2}} \theta=\frac{{c}^{\mathrm{2}} −{a}^{\mathrm{2}} }{{c}^{\mathrm{2}} −{b}^{\mathrm{2}} } \\ $$$${sin}\theta=\pm\sqrt{\frac{{c}^{\mathrm{2}} −{a}^{\mathrm{2}} }{{c}^{\mathrm{2}} −{b}^{\mathrm{2}} }} \\ $$
