Question Number 27853 by Poojadarshini94 last updated on 15/Jan/18
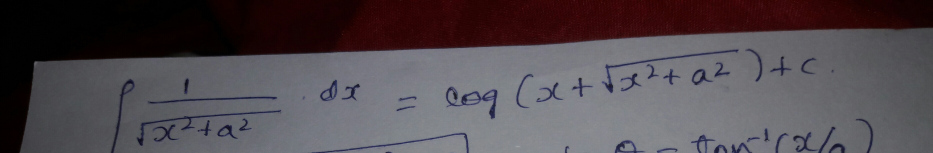
Commented by abdo imad last updated on 17/Jan/18
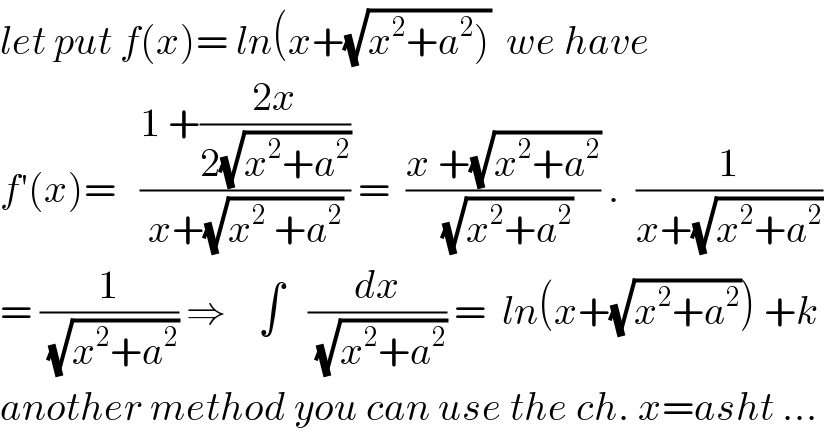
$${let}\:{put}\:{f}\left({x}\right)=\:{ln}\left({x}+\sqrt{\left.{x}^{\mathrm{2}} +{a}^{\mathrm{2}} \right)}\:\:{we}\:{have}\:\right. \\ $$$${f}'\left({x}\right)=^{\:\:} \:\:\frac{\mathrm{1}\:+\frac{\mathrm{2}{x}}{\mathrm{2}\sqrt{{x}^{\mathrm{2}} +{a}^{\mathrm{2}} }}}{{x}+\sqrt{{x}^{\mathrm{2}} \:+{a}^{\mathrm{2}} }}\:=\:\:\frac{{x}\:+\sqrt{{x}^{\mathrm{2}} +{a}^{\mathrm{2}} }}{\:\sqrt{{x}^{\mathrm{2}} +{a}^{\mathrm{2}} }}\:.\:\:\frac{\mathrm{1}}{{x}+\sqrt{{x}^{\mathrm{2}} +{a}^{\mathrm{2}} }} \\ $$$$=\:\frac{\mathrm{1}}{\:\sqrt{{x}^{\mathrm{2}} +{a}^{\mathrm{2}} }}\:\Rightarrow\:\:\:\:\int\:\:\:\frac{{dx}}{\:\sqrt{{x}^{\mathrm{2}} +{a}^{\mathrm{2}} }}\:=\:\:{ln}\left({x}+\sqrt{{x}^{\mathrm{2}} +{a}^{\mathrm{2}} }\right)\:+{k} \\ $$$${another}\:{method}\:{you}\:{can}\:{use}\:{the}\:{ch}.\:{x}={asht}\:… \\ $$
