Question Number 27870 by ajfour last updated on 15/Jan/18
Commented by ajfour last updated on 15/Jan/18
$${Q}.\mathrm{27818}\:{another}\:{solution} \\ $$
Answered by ajfour last updated on 15/Jan/18
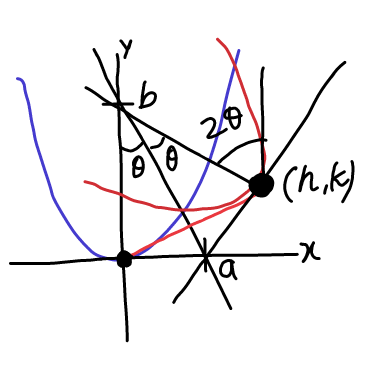
![translating the parabola y=Ax^2 to (h,k)≡(a+acos 2θ,asin 2θ) where tan θ=(a/b) ⇒ (h,k)≡[a+((a(b^2 −a^2 ))/(b^2 +a^2 )), ((2a^2 b)/(b^2 +a^2 ))] ≡[((2ab^2 )/(a^2 +b^2 )) ,((2a^2 b)/(a^2 +b^2 ))] y−k=A(x−h)^2 let us call this v=k+A(u−h)^2 say v=f(u) rotating it then by 2θ about(h,k) k+(y−k)cos 2θ−(x−h)sin 2θ =k+A[h+(x−h)cos 2θ+(y−k)sin 2θ−h]^2 ⇒(y−((2a^2 b)/(a^2 +b^2 )))(((b^2 −a^2 )/(a^2 +b^2 )))−(x−((2ab^2 )/(a^2 +b^2 )))(((2ab)/(a^2 +b^2 ))) =A[(x−((2ab^2 )/(a^2 +b^2 )))(((b^2 −a^2 )/(a^2 +b^2 )))+(y−((2a^2 b)/(a^2 +b^2 )))(((2ab)/(a^2 +b^2 )))]^2](https://www.tinkutara.com/question/Q27872.png)
$${translating}\:{the}\:{parabola}\:{y}={Ax}^{\mathrm{2}} \\ $$$${to}\:\left({h},{k}\right)\equiv\left({a}+{a}\mathrm{cos}\:\mathrm{2}\theta,{a}\mathrm{sin}\:\mathrm{2}\theta\right) \\ $$$$\:\:\:\:\:\:\:{where}\:\mathrm{tan}\:\theta=\frac{{a}}{{b}} \\ $$$$\Rightarrow\:\left({h},{k}\right)\equiv\left[{a}+\frac{{a}\left({b}^{\mathrm{2}} −{a}^{\mathrm{2}} \right)}{{b}^{\mathrm{2}} +{a}^{\mathrm{2}} },\:\frac{\mathrm{2}{a}^{\mathrm{2}} {b}}{{b}^{\mathrm{2}} +{a}^{\mathrm{2}} }\right] \\ $$$$\:\:\:\:\:\:\:\:\:\:\equiv\left[\frac{\mathrm{2}{ab}^{\mathrm{2}} }{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }\:,\frac{\mathrm{2}{a}^{\mathrm{2}} {b}}{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }\right]\: \\ $$$$\:\:{y}−{k}={A}\left({x}−{h}\right)^{\mathrm{2}} \\ $$$${let}\:{us}\:{call}\:{this} \\ $$$$\:\:{v}={k}+{A}\left({u}−{h}\right)^{\mathrm{2}} \:\:\:\:{say}\:{v}={f}\left({u}\right) \\ $$$${rotating}\:{it}\:{then}\:{by}\:\mathrm{2}\theta\:{about}\left({h},{k}\right) \\ $$$${k}+\left({y}−{k}\right)\mathrm{cos}\:\mathrm{2}\theta−\left({x}−{h}\right)\mathrm{sin}\:\mathrm{2}\theta \\ $$$$\:\:\:\:\:\:={k}+{A}\left[{h}+\left({x}−{h}\right)\mathrm{cos}\:\mathrm{2}\theta+\left({y}−{k}\right)\mathrm{sin}\:\mathrm{2}\theta−{h}\right]^{\mathrm{2}} \\ $$$$\Rightarrow\left({y}−\frac{\mathrm{2}{a}^{\mathrm{2}} {b}}{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }\right)\left(\frac{{b}^{\mathrm{2}} −{a}^{\mathrm{2}} }{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }\right)−\left({x}−\frac{\mathrm{2}{ab}^{\mathrm{2}} }{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }\right)\left(\frac{\mathrm{2}{ab}}{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }\right) \\ $$$$\:\:\:\:\:={A}\left[\left({x}−\frac{\mathrm{2}{ab}^{\mathrm{2}} }{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }\right)\left(\frac{{b}^{\mathrm{2}} −{a}^{\mathrm{2}} }{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }\right)+\left({y}−\frac{\mathrm{2}{a}^{\mathrm{2}} {b}}{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }\right)\left(\frac{\mathrm{2}{ab}}{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }\right)\right]^{\mathrm{2}} \\ $$
Commented by mrW2 last updated on 15/Jan/18

$${Very}\:{fine}\:{sir}! \\ $$
