Question-27997

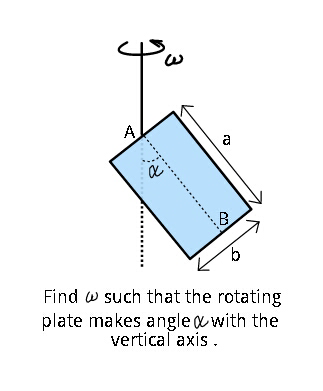
Question Number 27997 by ajfour last updated on 18/Jan/18

Commented by mrW2 last updated on 18/Jan/18

$$\omega=\sqrt{\frac{\mathrm{3}{g}}{\mathrm{2}{a}\:\mathrm{cos}\:\alpha}} \\ $$

Commented by ajfour last updated on 18/Jan/18

$${yes}\:{sir},\:{please}\:{see}\:{my}\:{solution} \\ $$$${when}\:{i}\:{post}.\:{Beforehand}\:{can}\:{i} \\ $$$${have}\:{some}\:{working}\:{steps}\:{to}\:{this} \\ $$$${answer}.. \\ $$

Commented by ajfour last updated on 18/Jan/18

What is the maximum value of ω for which the plate can stay in vertical plane ?

$${What}\:{is}\:{the}\:{maximum}\:{value}\:{of} \\ $$$$\omega\:{for}\:{which}\:{the}\:{plate}\:{can}\:{stay}\:{in} \\ $$$${vertical}\:{plane}\:? \\ $$

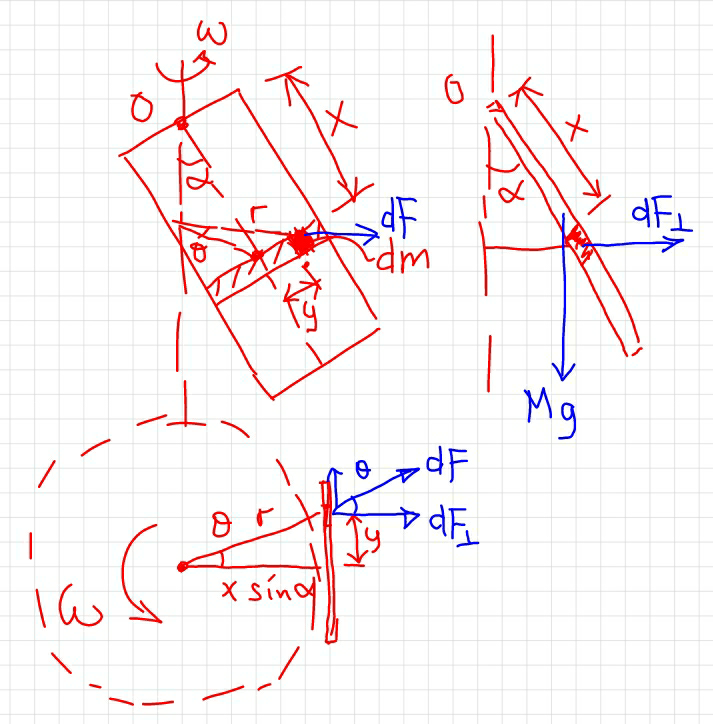
Answered by mrW2 last updated on 18/Jan/18

Commented by mrW2 last updated on 18/Jan/18

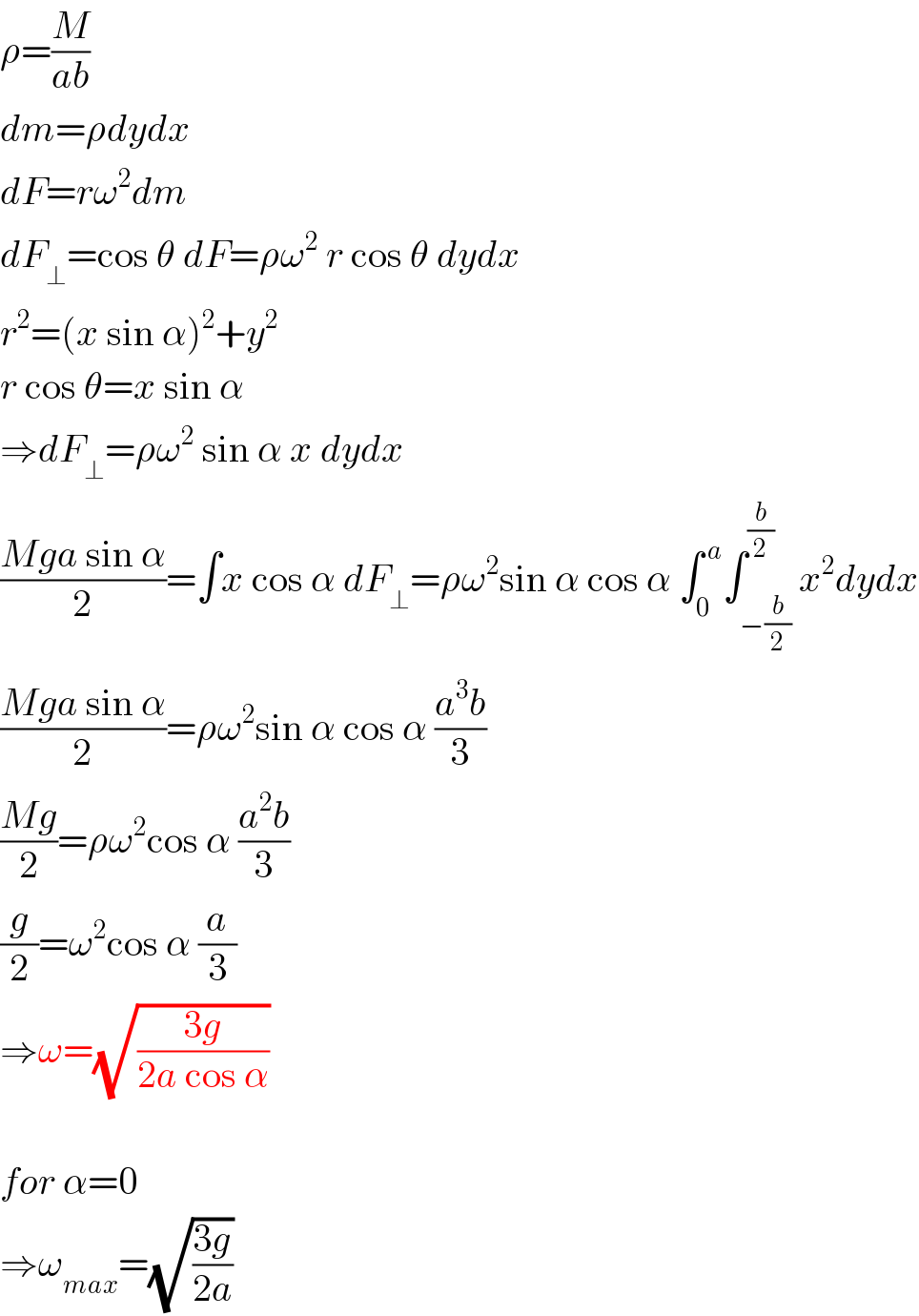
ρ=(M/(ab)) dm=ρdydx dF=rω^2 dm dF_⊥ =cos θ dF=ρω^2 r cos θ dydx r^2 =(x sin α)^2 +y^2 r cos θ=x sin α ⇒dF_⊥ =ρω^2 sin α x dydx ((Mga sin α)/2)=∫x cos α dF_⊥ =ρω^2 sin α cos α ∫_0 ^( a) ∫_(−(b/2)) ^(b/2) x^2 dydx ((Mga sin α)/2)=ρω^2 sin α cos α ((a^3 b)/3) ((Mg)/2)=ρω^2 cos α ((a^2 b)/3) (g/2)=ω^2 cos α (a/3) ⇒ω=(√((3g)/(2a cos α))) for α=0 ⇒ω_(max) =(√((3g)/(2a)))

$$\rho=\frac{{M}}{{ab}} \\ $$$${dm}=\rho{dydx} \\ $$$${dF}={r}\omega^{\mathrm{2}} {dm} \\ $$$${dF}_{\bot} =\mathrm{cos}\:\theta\:{dF}=\rho\omega^{\mathrm{2}} \:{r}\:\mathrm{cos}\:\theta\:{dydx} \\ $$$${r}^{\mathrm{2}} =\left({x}\:\mathrm{sin}\:\alpha\right)^{\mathrm{2}} +{y}^{\mathrm{2}} \\ $$$${r}\:\mathrm{cos}\:\theta={x}\:\mathrm{sin}\:\alpha \\ $$$$\Rightarrow{dF}_{\bot} =\rho\omega^{\mathrm{2}} \:\mathrm{sin}\:\alpha\:{x}\:{dydx} \\ $$$$\frac{{Mga}\:\mathrm{sin}\:\alpha}{\mathrm{2}}=\int{x}\:\mathrm{cos}\:\alpha\:{dF}_{\bot} =\rho\omega^{\mathrm{2}} \mathrm{sin}\:\alpha\:\mathrm{cos}\:\alpha\:\int_{\mathrm{0}} ^{\:{a}} \int_{−\frac{{b}}{\mathrm{2}}} ^{\frac{{b}}{\mathrm{2}}} {x}^{\mathrm{2}} {dydx} \\ $$$$\frac{{Mga}\:\mathrm{sin}\:\alpha}{\mathrm{2}}=\rho\omega^{\mathrm{2}} \mathrm{sin}\:\alpha\:\mathrm{cos}\:\alpha\:\frac{{a}^{\mathrm{3}} {b}}{\mathrm{3}} \\ $$$$\frac{{Mg}}{\mathrm{2}}=\rho\omega^{\mathrm{2}} \mathrm{cos}\:\alpha\:\frac{{a}^{\mathrm{2}} {b}}{\mathrm{3}} \\ $$$$\frac{{g}}{\mathrm{2}}=\omega^{\mathrm{2}} \mathrm{cos}\:\alpha\:\frac{{a}}{\mathrm{3}} \\ $$$$\Rightarrow\omega=\sqrt{\frac{\mathrm{3}{g}}{\mathrm{2}{a}\:\mathrm{cos}\:\alpha}} \\ $$$$ \\ $$$${for}\:\alpha=\mathrm{0} \\ $$$$\Rightarrow\omega_{{max}} =\sqrt{\frac{\mathrm{3}{g}}{\mathrm{2}{a}}} \\ $$

Commented by ajfour last updated on 18/Jan/18

Thank you too much Sir. I enjoyed thoroughly following the solution Sir.

Facebook Tweet Pin

Leave a Reply Cancel reply