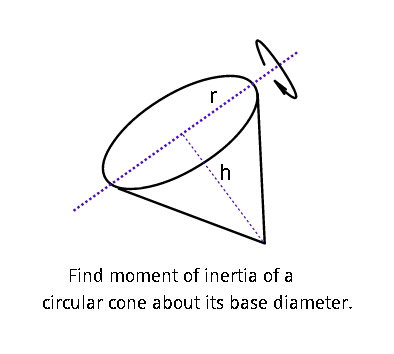
Question Number 28027 by ajfour last updated on 18/Jan/18
Answered by mrW2 last updated on 19/Jan/18
)^2 R^2 dx =((ρπhR^4 )/4)∫_0 ^( h) [((4h^2 )/R^2 )((x/h))^2 +(1−(x/h))^2 ](1−(x/h))^2 d((x/h)) =((ρπhR^4 )/4)∫_0 ^( 1) [((4h^2 )/R^2 )(1−s)^2 +s^2 ]s^2 ds =((ρπhR^4 )/4)∫_0 ^( 1) [((4h^2 )/R^2 )(s^2 −2s^3 +s^4 )+s^4 ]ds =((ρπhR^4 )/4)[((4h^2 )/R^2 )((s^3 /3)−(s^4 /2)+(s^5 /5))+(s^5 /5)]_0 ^1 =((ρπhR^4 )/4)[((4h^2 )/R^2 )((1/3)−(1/2)+(1/5))+(1/5)] =((ρπhR^4 )/4)(((2h^2 )/(15R^2 ))+(1/5)) =((ρπhR^2 (2h^2 +3R^2 ))/(60)) =((ρπhR^2 )/3)×(((2h^2 +3R^2 ))/(20)) ⇒I=((M(2h^2 +3R^2 ))/(20))](https://www.tinkutara.com/question/Q28030.png)
$${radius}\:{of}\:{base}\:{circle}\:={R} \\ $$$${radius}\:{of}\:{disc}\:{in}\:{distance}\:{x}\:{from}\:{the} \\ $$$${base}\:{is}\:{r}=\frac{{h}−{x}}{{h}}×{R}=\left(\mathrm{1}−\frac{{x}}{{h}}\right){R} \\ $$$${mass}\:{of}\:{disc}\:{is}\:{dm}=\rho\pi{r}^{\mathrm{2}} {dx} \\ $$$${moment}\:{of}\:{inertia}\:{of}\:{disc}\:{about}\:{its}\:{own}\:{diameter} \\ $$$${is}\:{I}_{\mathrm{0}} =\frac{{r}^{\mathrm{2}} {dm}}{\mathrm{4}},\:{and}\:{about}\:{the}\:{diameter}\:{of} \\ $$$${base}\:{is}\:{then}\:{dI}={x}^{\mathrm{2}} {dm}+\frac{{r}^{\mathrm{2}} {dm}}{\mathrm{4}} \\ $$$${I}=\int^{\:} \left({x}^{\mathrm{2}} {dm}+\frac{{r}^{\mathrm{2}} {dm}}{\mathrm{4}}\right)=\int\left({x}^{\mathrm{2}} +\frac{{r}^{\mathrm{2}} }{\mathrm{4}}\right){dm} \\ $$$$=\int_{\mathrm{0}} ^{\:{h}} \left({x}^{\mathrm{2}} +\frac{{r}^{\mathrm{2}} }{\mathrm{4}}\right)\rho\pi{r}^{\mathrm{2}} {dx} \\ $$$$=\frac{\rho\pi}{\mathrm{4}}\int_{\mathrm{0}} ^{\:{h}} \left(\mathrm{4}{x}^{\mathrm{2}} +{r}^{\mathrm{2}} \right){r}^{\mathrm{2}} {dx} \\ $$$$=\frac{\rho\pi}{\mathrm{4}}\int_{\mathrm{0}} ^{\:{h}} \left[\mathrm{4}{x}^{\mathrm{2}} +\left(\mathrm{1}−\frac{{x}}{{h}}\right)^{\mathrm{2}} {R}^{\mathrm{2}} \right]\left(\mathrm{1}−\frac{{x}}{{h}}\right)^{\mathrm{2}} {R}^{\mathrm{2}} {dx} \\ $$$$=\frac{\rho\pi{hR}^{\mathrm{4}} }{\mathrm{4}}\int_{\mathrm{0}} ^{\:{h}} \left[\frac{\mathrm{4}{h}^{\mathrm{2}} }{{R}^{\mathrm{2}} }\left(\frac{{x}}{{h}}\right)^{\mathrm{2}} +\left(\mathrm{1}−\frac{{x}}{{h}}\right)^{\mathrm{2}} \right]\left(\mathrm{1}−\frac{{x}}{{h}}\right)^{\mathrm{2}} {d}\left(\frac{{x}}{{h}}\right) \\ $$$$=\frac{\rho\pi{hR}^{\mathrm{4}} }{\mathrm{4}}\int_{\mathrm{0}} ^{\:\mathrm{1}} \left[\frac{\mathrm{4}{h}^{\mathrm{2}} }{{R}^{\mathrm{2}} }\left(\mathrm{1}−{s}\right)^{\mathrm{2}} +{s}^{\mathrm{2}} \right]{s}^{\mathrm{2}} {ds} \\ $$$$=\frac{\rho\pi{hR}^{\mathrm{4}} }{\mathrm{4}}\int_{\mathrm{0}} ^{\:\mathrm{1}} \left[\frac{\mathrm{4}{h}^{\mathrm{2}} }{{R}^{\mathrm{2}} }\left({s}^{\mathrm{2}} −\mathrm{2}{s}^{\mathrm{3}} +{s}^{\mathrm{4}} \right)+{s}^{\mathrm{4}} \right]{ds} \\ $$$$=\frac{\rho\pi{hR}^{\mathrm{4}} }{\mathrm{4}}\left[\frac{\mathrm{4}{h}^{\mathrm{2}} }{{R}^{\mathrm{2}} }\left(\frac{{s}^{\mathrm{3}} }{\mathrm{3}}−\frac{{s}^{\mathrm{4}} }{\mathrm{2}}+\frac{{s}^{\mathrm{5}} }{\mathrm{5}}\right)+\frac{{s}^{\mathrm{5}} }{\mathrm{5}}\right]_{\mathrm{0}} ^{\mathrm{1}} \\ $$$$=\frac{\rho\pi{hR}^{\mathrm{4}} }{\mathrm{4}}\left[\frac{\mathrm{4}{h}^{\mathrm{2}} }{{R}^{\mathrm{2}} }\left(\frac{\mathrm{1}}{\mathrm{3}}−\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{5}}\right)+\frac{\mathrm{1}}{\mathrm{5}}\right] \\ $$$$=\frac{\rho\pi{hR}^{\mathrm{4}} }{\mathrm{4}}\left(\frac{\mathrm{2}{h}^{\mathrm{2}} }{\mathrm{15}{R}^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{5}}\right) \\ $$$$=\frac{\rho\pi{hR}^{\mathrm{2}} \left(\mathrm{2}{h}^{\mathrm{2}} +\mathrm{3}{R}^{\mathrm{2}} \right)}{\mathrm{60}} \\ $$$$=\frac{\rho\pi{hR}^{\mathrm{2}} }{\mathrm{3}}×\frac{\left(\mathrm{2}{h}^{\mathrm{2}} +\mathrm{3}{R}^{\mathrm{2}} \right)}{\mathrm{20}} \\ $$$$\Rightarrow{I}=\frac{{M}\left(\mathrm{2}{h}^{\mathrm{2}} +\mathrm{3}{R}^{\mathrm{2}} \right)}{\mathrm{20}} \\ $$
Commented by ajfour last updated on 19/Jan/18

$${Great}\:{so}\:{quick}\:{Sir}!\:{you}\:{are} \\ $$$${wonderful}.\:{Answer}\:{is}\:{right}\:{sir}. \\ $$$${I}\:{havefollowed}\:{it}\:{carefully},{Sir}\:. \\ $$$${the}\:{integral}\:{is}\:{e}^{{x}} {cellently}\:{handled}\:! \\ $$
