Question Number 28113 by ajfour last updated on 20/Jan/18
Commented by ajfour last updated on 20/Jan/18

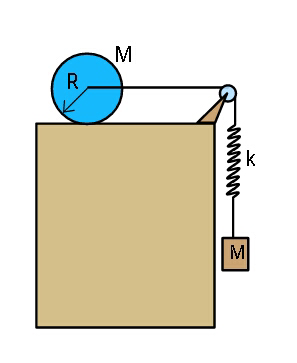
$${If}\:{system}\:{of}\:{disc},\:{spring},\:{and} \\ $$$${block}\:{of}\:{mass}\:\boldsymbol{{m}},\:{be}\:{released}\:{from} \\ $$$${rest}\:{with}\:{spring}\:{in}\:{natural}\:{length}, \\ $$$$\left({friction}\:{being}\:{sufficent}\:{to}\right. \\ $$$$\left.{prevent}\:{slipping}\right)\:{find}\:{maximum} \\ $$$${deformation}\:{in}\:{spring}. \\ $$$${Also}\:{find}\:{the}\:{minimum}\:{coefficient} \\ $$$${of}\:{friction}\:{required}\:{to}\:{prevent} \\ $$$${slipping}\:{of}\:{disc}\:{on}\:{the}\:{fixed} \\ $$$${platform}. \\ $$
Answered by mrW2 last updated on 21/Jan/18
![x_1 =displacement of block a_1 =acceleration of block=(d^2 x_1 /dt^2 ) x_2 =displacement of disc a_2 =acceleration of disc=(d^2 x_2 /dt^2 ) T=force in spring e=deformation in spring=x_1 −x_2 Spring: T=ke=k(x_1 −x_2 ) ⇒(d^2 T/dt^2 )=k(a_1 −a_2 ) Block: mg−T=ma_1 ⇒a_1 =g−(T/m) Disc: TR=I_2 α_2 =(((mR^2 )/2)+mR^2 )×(a_2 /R)=((3mR)/2)×a_2 ⇒a_2 =((2T)/(3m)) ⇒(d^2 T/dt^2 )=k(a_1 −a_2 )=k(g−(T/m)−((2T)/(3m)))=(k/m)(mg−((5T)/3)) ⇒(d^2 T/dt^2 )=(k/m)(mg−((5T)/3)) let S=mg−((5T)/3) (d^2 S/dt^2 )=−(5/3)×(d^2 T/dt^2 ) ⇒−(3/5)(d^2 S/dt^2 )=(k/m)S ⇒(d^2 S/dt^2 )+((5k)/(3m))S=0 ⇒S=c_1 sin ωt+c_2 cos ωt with ω=(√((5k)/(3m))) ⇒T=(3/5)(mg−S)=(3/5)(mg−c_1 sin ωt−c_2 cos ωt) ⇒(dT/dt)=(3/5)(−c_1 cos ωt+c_2 sin ωt)ω at t=0: T=0 and (dT/dt)=k(v_1 −v_2 )=0 mg−c_2 =0⇒c_2 =mg ⇒c_1 =0 ⇒T=((3mg)/5)(1− cos ωt) ⇒T_(max) =((6mg)/5) at ωt=(2n−1)π or t=(2n−1)π(√((3m)/(5k))) ⇒e_(max) =((6mg)/(5k)) T−f=ma_2 f=T−ma_2 =T−((2T)/3)=(T/3)≤μmg ⇒μ≥(T_(max) /(3mg))=((6mg)/(3×5mg))=(2/5)=0.4 a_1 =g−((3g)/5)(1−cos ωt)=(g/5)(2+3cos ωt) v_1 =(g/5)(2t+(3/ω)sin ωt) ⇒x_1 =(g/5)[t^2 +(3/ω^2 )(1−cos ωt)] a_2 =((2g)/5)(1−cos ωt) ⇒v_2 =((2g)/5)(t−(1/ω)sin ωt) ⇒x_2 =(g/5)[t^2 −(2/ω^2 )(1−cos ωt)] we see the system is in vibration. the force in spring varies between 0 and ((6mg)/5), about the mean value ((3mg)/5). after the vibration is vanished, the force in spring remains constant, the spring acts as normal string, block and disc have the same acceleration: a_1 =a_2 g−(T/m)=((2T)/(3m)) ⇒T=((3mg)/5)=mean value of vibration ⇒e=((3mg)/5)](https://www.tinkutara.com/question/Q28133.png)
$${x}_{\mathrm{1}} ={displacement}\:{of}\:{block} \\ $$$${a}_{\mathrm{1}} ={acceleration}\:{of}\:{block}=\frac{{d}^{\mathrm{2}} {x}_{\mathrm{1}} }{{dt}^{\mathrm{2}} } \\ $$$${x}_{\mathrm{2}} ={displacement}\:{of}\:{disc} \\ $$$${a}_{\mathrm{2}} ={acceleration}\:{of}\:{disc}=\frac{{d}^{\mathrm{2}} {x}_{\mathrm{2}} }{{dt}^{\mathrm{2}} } \\ $$$${T}={force}\:{in}\:{spring} \\ $$$${e}={deformation}\:{in}\:{spring}={x}_{\mathrm{1}} −{x}_{\mathrm{2}} \\ $$$$ \\ $$$${Spring}: \\ $$$${T}={ke}={k}\left({x}_{\mathrm{1}} −{x}_{\mathrm{2}} \right) \\ $$$$\Rightarrow\frac{{d}^{\mathrm{2}} {T}}{{dt}^{\mathrm{2}} }={k}\left({a}_{\mathrm{1}} −{a}_{\mathrm{2}} \right) \\ $$$$ \\ $$$${Block}: \\ $$$${mg}−{T}={ma}_{\mathrm{1}} \\ $$$$\Rightarrow{a}_{\mathrm{1}} ={g}−\frac{{T}}{{m}} \\ $$$$ \\ $$$${Disc}: \\ $$$${TR}={I}_{\mathrm{2}} \alpha_{\mathrm{2}} =\left(\frac{{mR}^{\mathrm{2}} }{\mathrm{2}}+{mR}^{\mathrm{2}} \right)×\frac{{a}_{\mathrm{2}} }{{R}}=\frac{\mathrm{3}{mR}}{\mathrm{2}}×{a}_{\mathrm{2}} \\ $$$$\Rightarrow{a}_{\mathrm{2}} =\frac{\mathrm{2}{T}}{\mathrm{3}{m}} \\ $$$$ \\ $$$$\Rightarrow\frac{{d}^{\mathrm{2}} {T}}{{dt}^{\mathrm{2}} }={k}\left({a}_{\mathrm{1}} −{a}_{\mathrm{2}} \right)={k}\left({g}−\frac{{T}}{{m}}−\frac{\mathrm{2}{T}}{\mathrm{3}{m}}\right)=\frac{{k}}{{m}}\left({mg}−\frac{\mathrm{5}{T}}{\mathrm{3}}\right) \\ $$$$\Rightarrow\frac{{d}^{\mathrm{2}} {T}}{{dt}^{\mathrm{2}} }=\frac{{k}}{{m}}\left({mg}−\frac{\mathrm{5}{T}}{\mathrm{3}}\right) \\ $$$${let}\:{S}={mg}−\frac{\mathrm{5}{T}}{\mathrm{3}} \\ $$$$\frac{{d}^{\mathrm{2}} {S}}{{dt}^{\mathrm{2}} }=−\frac{\mathrm{5}}{\mathrm{3}}×\frac{{d}^{\mathrm{2}} {T}}{{dt}^{\mathrm{2}} } \\ $$$$\Rightarrow−\frac{\mathrm{3}}{\mathrm{5}}\frac{{d}^{\mathrm{2}} {S}}{{dt}^{\mathrm{2}} }=\frac{{k}}{{m}}{S} \\ $$$$\Rightarrow\frac{{d}^{\mathrm{2}} {S}}{{dt}^{\mathrm{2}} }+\frac{\mathrm{5}{k}}{\mathrm{3}{m}}{S}=\mathrm{0} \\ $$$$\Rightarrow{S}={c}_{\mathrm{1}} \:\mathrm{sin}\:\omega{t}+{c}_{\mathrm{2}} \:\mathrm{cos}\:\omega{t} \\ $$$${with}\:\omega=\sqrt{\frac{\mathrm{5}{k}}{\mathrm{3}{m}}} \\ $$$$\Rightarrow{T}=\frac{\mathrm{3}}{\mathrm{5}}\left({mg}−{S}\right)=\frac{\mathrm{3}}{\mathrm{5}}\left({mg}−{c}_{\mathrm{1}} \:\mathrm{sin}\:\omega{t}−{c}_{\mathrm{2}} \:\mathrm{cos}\:\omega{t}\right) \\ $$$$\Rightarrow\frac{{dT}}{{dt}}=\frac{\mathrm{3}}{\mathrm{5}}\left(−{c}_{\mathrm{1}} \:\mathrm{cos}\:\omega{t}+{c}_{\mathrm{2}} \:\mathrm{sin}\:\omega{t}\right)\omega \\ $$$${at}\:{t}=\mathrm{0}:\:{T}=\mathrm{0}\:{and}\:\frac{{dT}}{{dt}}={k}\left({v}_{\mathrm{1}} −{v}_{\mathrm{2}} \right)=\mathrm{0} \\ $$$${mg}−{c}_{\mathrm{2}} =\mathrm{0}\Rightarrow{c}_{\mathrm{2}} ={mg} \\ $$$$\Rightarrow{c}_{\mathrm{1}} =\mathrm{0} \\ $$$$\Rightarrow{T}=\frac{\mathrm{3}{mg}}{\mathrm{5}}\left(\mathrm{1}−\:\mathrm{cos}\:\omega{t}\right) \\ $$$$\Rightarrow{T}_{{max}} =\frac{\mathrm{6}{mg}}{\mathrm{5}}\:{at}\:\omega{t}=\left(\mathrm{2}{n}−\mathrm{1}\right)\pi\:{or}\:{t}=\left(\mathrm{2}{n}−\mathrm{1}\right)\pi\sqrt{\frac{\mathrm{3}{m}}{\mathrm{5}{k}}} \\ $$$$\Rightarrow{e}_{{max}} =\frac{\mathrm{6}{mg}}{\mathrm{5}{k}} \\ $$$$ \\ $$$${T}−{f}={ma}_{\mathrm{2}} \\ $$$${f}={T}−{ma}_{\mathrm{2}} ={T}−\frac{\mathrm{2}{T}}{\mathrm{3}}=\frac{{T}}{\mathrm{3}}\leqslant\mu{mg} \\ $$$$\Rightarrow\mu\geqslant\frac{{T}_{{max}} }{\mathrm{3}{mg}}=\frac{\mathrm{6}{mg}}{\mathrm{3}×\mathrm{5}{mg}}=\frac{\mathrm{2}}{\mathrm{5}}=\mathrm{0}.\mathrm{4} \\ $$$$ \\ $$$${a}_{\mathrm{1}} ={g}−\frac{\mathrm{3}{g}}{\mathrm{5}}\left(\mathrm{1}−\mathrm{cos}\:\omega{t}\right)=\frac{{g}}{\mathrm{5}}\left(\mathrm{2}+\mathrm{3cos}\:\omega{t}\right) \\ $$$${v}_{\mathrm{1}} =\frac{{g}}{\mathrm{5}}\left(\mathrm{2}{t}+\frac{\mathrm{3}}{\omega}\mathrm{sin}\:\omega{t}\right) \\ $$$$\Rightarrow{x}_{\mathrm{1}} =\frac{{g}}{\mathrm{5}}\left[{t}^{\mathrm{2}} +\frac{\mathrm{3}}{\omega^{\mathrm{2}} }\left(\mathrm{1}−\mathrm{cos}\:\omega{t}\right)\right] \\ $$$$ \\ $$$${a}_{\mathrm{2}} =\frac{\mathrm{2}{g}}{\mathrm{5}}\left(\mathrm{1}−\mathrm{cos}\:\omega{t}\right) \\ $$$$\Rightarrow{v}_{\mathrm{2}} =\frac{\mathrm{2}{g}}{\mathrm{5}}\left({t}−\frac{\mathrm{1}}{\omega}\mathrm{sin}\:\omega{t}\right) \\ $$$$\Rightarrow{x}_{\mathrm{2}} =\frac{{g}}{\mathrm{5}}\left[{t}^{\mathrm{2}} −\frac{\mathrm{2}}{\omega^{\mathrm{2}} }\left(\mathrm{1}−\mathrm{cos}\:\omega{t}\right)\right] \\ $$$$ \\ $$$${we}\:{see}\:{the}\:{system}\:{is}\:{in}\:{vibration}.\:{the} \\ $$$${force}\:{in}\:{spring}\:{varies}\:{between}\:\mathrm{0}\:{and} \\ $$$$\frac{\mathrm{6}{mg}}{\mathrm{5}},\:{about}\:{the}\:{mean}\:{value}\:\frac{\mathrm{3}{mg}}{\mathrm{5}}. \\ $$$${after}\:{the}\:{vibration}\:{is}\:{vanished},\:{the} \\ $$$${force}\:{in}\:{spring}\:{remains}\:{constant}, \\ $$$${the}\:{spring}\:{acts}\:{as}\:{normal}\:{string}, \\ $$$${block}\:{and}\:{disc}\:{have}\:{the}\:{same} \\ $$$${acceleration}: \\ $$$${a}_{\mathrm{1}} ={a}_{\mathrm{2}} \\ $$$${g}−\frac{{T}}{{m}}=\frac{\mathrm{2}{T}}{\mathrm{3}{m}} \\ $$$$\Rightarrow{T}=\frac{\mathrm{3}{mg}}{\mathrm{5}}={mean}\:{value}\:{of}\:{vibration} \\ $$$$\Rightarrow{e}=\frac{\mathrm{3}{mg}}{\mathrm{5}} \\ $$
Commented by ajfour last updated on 21/Jan/18

$${Thank}\:{you}\:{sir}. \\ $$$$\mathcal{ENTIRELY}\:\:\mathcal{B}{eautiful}\:\mathcal{S}{ir}\:! \\ $$
