Question Number 28211 by ajfour last updated on 22/Jan/18

Commented by math solver last updated on 22/Jan/18

$${thank}\:{you}\:{sir}! \\ $$
Commented by math solver last updated on 22/Jan/18

$${sir},\:{i}\:{think}\:{they}\:{are}\:{referring}\: \\ $$$${max}.\:{amplitude}\:{as}\:{max}.\:{argument}. \\ $$
Commented by ajfour last updated on 22/Jan/18

$${Q}.\mathrm{28189}\:\:\left({solution}\right) \\ $$$${the}\:{blue}\:{region}\:{is}\:{A}\cap{B}\cap{C}. \\ $$$$\mathrm{6}\:{points}\:{with}\:{integral}\:{coordinates}, \\ $$$${is}\:{fine}\:{but}\:{point}\:{having}\:{maximum} \\ $$$${amplitude}\:\left({not}\:{magnitude}\right)\:{would} \\ $$$${be}\:…?\:\:\left({you}\:{can}\:{see}\:{for}\:{yourself}\right. \\ $$$$\left.{math}\:{solver}\:\right). \\ $$
Commented by math solver last updated on 22/Jan/18
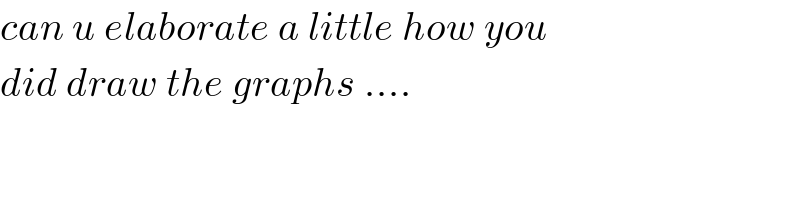
$${can}\:{u}\:{elaborate}\:{a}\:{little}\:{how}\:{you}\: \\ $$$${did}\:{draw}\:{the}\:{graphs}\:…. \\ $$
Commented by ajfour last updated on 22/Jan/18
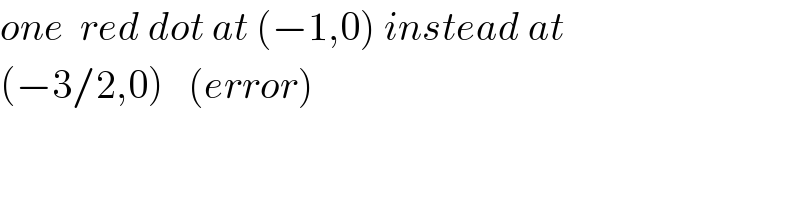
$${one}\:\:{red}\:{dot}\:{at}\:\left(−\mathrm{1},\mathrm{0}\right)\:{instead}\:{at} \\ $$$$\left(−\mathrm{3}/\mathrm{2},\mathrm{0}\right)\:\:\:\left({error}\right) \\ $$
Commented by ajfour last updated on 22/Jan/18
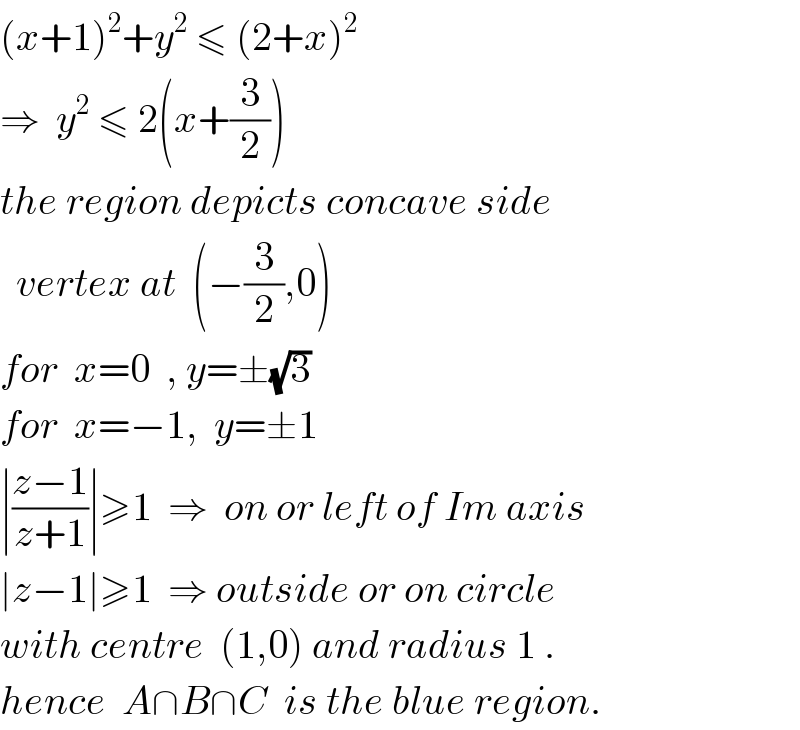
$$\left({x}+\mathrm{1}\right)^{\mathrm{2}} +{y}^{\mathrm{2}} \:\leqslant\:\left(\mathrm{2}+{x}\right)^{\mathrm{2}} \\ $$$$\Rightarrow\:\:{y}^{\mathrm{2}} \:\leqslant\:\mathrm{2}\left({x}+\frac{\mathrm{3}}{\mathrm{2}}\right) \\ $$$${the}\:{region}\:{depicts}\:{concave}\:{side} \\ $$$$\:\:{vertex}\:{at}\:\:\left(−\frac{\mathrm{3}}{\mathrm{2}},\mathrm{0}\right) \\ $$$${for}\:\:{x}=\mathrm{0}\:\:,\:{y}=\pm\sqrt{\mathrm{3}} \\ $$$${for}\:\:{x}=−\mathrm{1},\:\:{y}=\pm\mathrm{1} \\ $$$$\mid\frac{{z}−\mathrm{1}}{{z}+\mathrm{1}}\mid\geqslant\mathrm{1}\:\:\Rightarrow\:\:{on}\:{or}\:{left}\:{of}\:{Im}\:{axis} \\ $$$$\mid{z}−\mathrm{1}\mid\geqslant\mathrm{1}\:\:\Rightarrow\:{outside}\:{or}\:{on}\:{circle} \\ $$$${with}\:{centre}\:\:\left(\mathrm{1},\mathrm{0}\right)\:{and}\:{radius}\:\mathrm{1}\:. \\ $$$${hence}\:\:{A}\cap{B}\cap{C}\:\:{is}\:{the}\:{blue}\:{region}. \\ $$
