Question Number 28278 by ajfour last updated on 23/Jan/18

Commented by ajfour last updated on 23/Jan/18

$${If}\:{y}={mx}+{c}\:\:\:{be}\:{tangent}\:{to}\:{the} \\ $$$${ellipse}\:\frac{{x}^{\mathrm{2}} }{{a}^{\mathrm{2}} }+\frac{{y}^{\mathrm{2}} }{{b}^{\mathrm{2}} }=\mathrm{1}\:,\:{find}\:{the} \\ $$$${condition}\:{for}\:{tangency}\:{of}\:{the}\: \\ $$$${given}\:{line}\:{to}\:{the}\:{ellipse}. \\ $$
Answered by ajfour last updated on 23/Jan/18
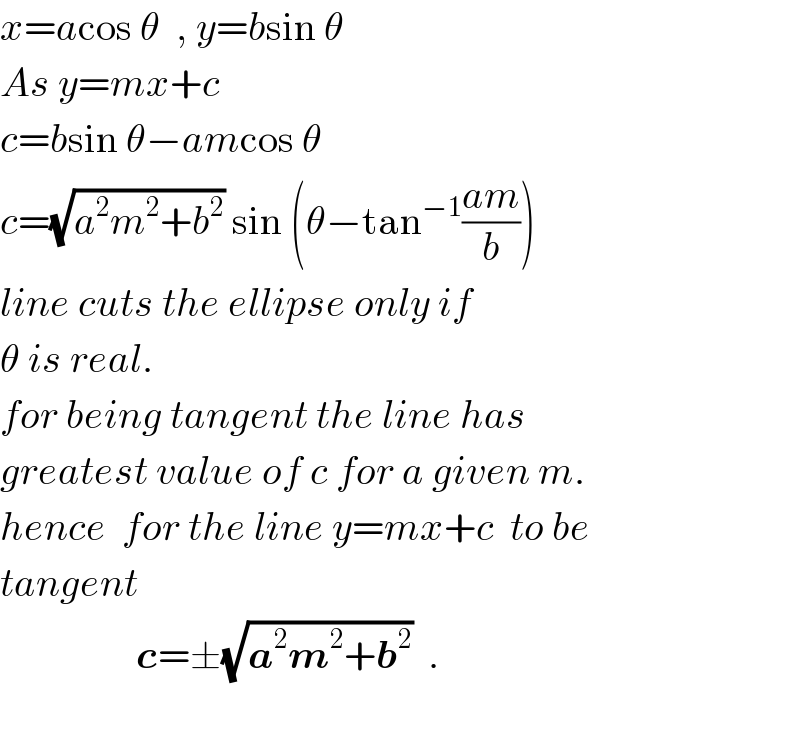
$${x}={a}\mathrm{cos}\:\theta\:\:,\:{y}={b}\mathrm{sin}\:\theta \\ $$$${As}\:{y}={mx}+{c} \\ $$$${c}={b}\mathrm{sin}\:\theta−{am}\mathrm{cos}\:\theta \\ $$$${c}=\sqrt{{a}^{\mathrm{2}} {m}^{\mathrm{2}} +{b}^{\mathrm{2}} }\:\mathrm{sin}\:\left(\theta−\mathrm{tan}^{−\mathrm{1}} \frac{{am}}{{b}}\right) \\ $$$${line}\:{cuts}\:{the}\:{ellipse}\:{only}\:{if} \\ $$$$\theta\:{is}\:{real}. \\ $$$${for}\:{being}\:{tangent}\:{the}\:{line}\:{has} \\ $$$${greatest}\:{value}\:{of}\:{c}\:{for}\:{a}\:{given}\:{m}. \\ $$$${hence}\:\:{for}\:{the}\:{line}\:{y}={mx}+{c}\:\:{to}\:{be} \\ $$$${tangent} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\boldsymbol{{c}}=\pm\sqrt{\boldsymbol{{a}}^{\mathrm{2}} \boldsymbol{{m}}^{\mathrm{2}} +\boldsymbol{{b}}^{\mathrm{2}} }\:\:. \\ $$$$ \\ $$
Commented by mrW2 last updated on 23/Jan/18

$${Thank}\:{you}\:{sir}! \\ $$
Answered by mrW2 last updated on 23/Jan/18

$${Let}'{s}\:{see}\:{the}\:{general}\:{case}\:{and}\:{find} \\ $$$${the}\:{condition}\:{when}\:{the}\:{line} \\ $$$${px}+{qy}+{r}=\mathrm{0} \\ $$$${tangents}\:{the}\:{ellipse} \\ $$$$\frac{{x}^{\mathrm{2}} }{{a}^{\mathrm{2}} }+\frac{{y}^{\mathrm{2}} }{{b}^{\mathrm{2}} }=\mathrm{1}. \\ $$$$ \\ $$$${The}\:{intersection}\:{points}\:{from}\:{the}\:{line} \\ $$$${and}\:{the}\:{ellipse}\:{are}\:{the}\:{solutions}\:{of} \\ $$$$\begin{cases}{{px}+{qy}+{r}=\mathrm{0}\:\:\:\:…\left({i}\right)}\\{\frac{{x}^{\mathrm{2}} }{{a}^{\mathrm{2}} }+\frac{{y}^{\mathrm{2}} }{{b}^{\mathrm{2}} }=\mathrm{1}\:\:\:\:…\left({ii}\right)}\end{cases} \\ $$$${from}\:\left({i}\right): \\ $$$${qy}=−{px}−{r} \\ $$$${from}\:\left({ii}\right): \\ $$$${b}^{\mathrm{2}} {q}^{\mathrm{2}} {x}^{\mathrm{2}} +{a}^{\mathrm{2}} {q}^{\mathrm{2}} {y}^{\mathrm{2}} ={a}^{\mathrm{2}} {b}^{\mathrm{2}} {q}^{\mathrm{2}} \\ $$$$\Rightarrow{b}^{\mathrm{2}} {q}^{\mathrm{2}} {x}^{\mathrm{2}} +{a}^{\mathrm{2}} \left(−{px}−{r}\right)^{\mathrm{2}} ={a}^{\mathrm{2}} {b}^{\mathrm{2}} {q}^{\mathrm{2}} \\ $$$$\Rightarrow{b}^{\mathrm{2}} {q}^{\mathrm{2}} {x}^{\mathrm{2}} +{a}^{\mathrm{2}} \left({p}^{\mathrm{2}} {x}^{\mathrm{2}} +\mathrm{2}{prx}+{r}^{\mathrm{2}} \right)={a}^{\mathrm{2}} {b}^{\mathrm{2}} {q}^{\mathrm{2}} \\ $$$$\Rightarrow\left({a}^{\mathrm{2}} {p}^{\mathrm{2}} +{b}^{\mathrm{2}} {q}^{\mathrm{2}} \right){x}^{\mathrm{2}} +\mathrm{2}{a}^{\mathrm{2}} {prx}+{a}^{\mathrm{2}} \left({r}^{\mathrm{2}} −{b}^{\mathrm{2}} {q}^{\mathrm{2}} \right)=\mathrm{0} \\ $$$$ \\ $$$${When}\:{the}\:{line}\:{only}\:{tangents}\:{the}\:{ellipse}, \\ $$$${the}\:{eqn}.\:{above}\:{should}\:{have}\:{one}\:{and} \\ $$$${only}\:{one}\:{solution}.\:{That}\:{means} \\ $$$$\Delta=\mathrm{4}{a}^{\mathrm{4}} {p}^{\mathrm{2}} {r}^{\mathrm{2}} −\mathrm{4}\left({a}^{\mathrm{2}} {p}^{\mathrm{2}} +{b}^{\mathrm{2}} {q}^{\mathrm{2}} \right){a}^{\mathrm{2}} \left({r}^{\mathrm{2}} −{b}^{\mathrm{2}} {q}^{\mathrm{2}} \right)=\mathrm{0} \\ $$$$\Rightarrow{a}^{\mathrm{2}} {p}^{\mathrm{2}} {r}^{\mathrm{2}} =\left({a}^{\mathrm{2}} {p}^{\mathrm{2}} +{b}^{\mathrm{2}} {q}^{\mathrm{2}} \right)\left({r}^{\mathrm{2}} −{b}^{\mathrm{2}} {q}^{\mathrm{2}} \right) \\ $$$$\Rightarrow{a}^{\mathrm{2}} {p}^{\mathrm{2}} {r}^{\mathrm{2}} ={a}^{\mathrm{2}} {p}^{\mathrm{2}} {r}^{\mathrm{2}} +{b}^{\mathrm{2}} {q}^{\mathrm{2}} {r}^{\mathrm{2}} −{a}^{\mathrm{2}} {b}^{\mathrm{2}} {p}^{\mathrm{2}} {q}^{\mathrm{2}} −{b}^{\mathrm{4}} {q}^{\mathrm{4}} \\ $$$$\Rightarrow{r}^{\mathrm{2}} ={a}^{\mathrm{2}} {p}^{\mathrm{2}} +{b}^{\mathrm{2}} {q}^{\mathrm{2}} \\ $$$${or} \\ $$$$\Rightarrow\left({ap}\right)^{\mathrm{2}} +\left({bq}\right)^{\mathrm{2}} ={r}^{\mathrm{2}} \\ $$
Commented by ajfour last updated on 23/Jan/18
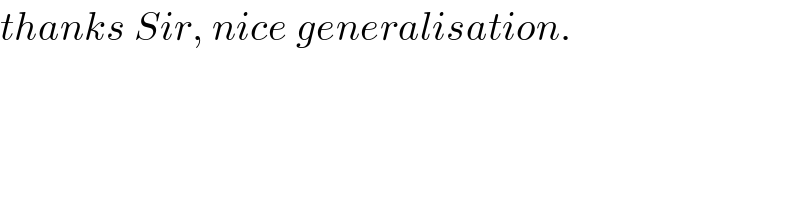
$${thanks}\:{Sir},\:{nice}\:{generalisation}. \\ $$
