Question-28288

Question Number 28288 by Mr eaay last updated on 23/Jan/18

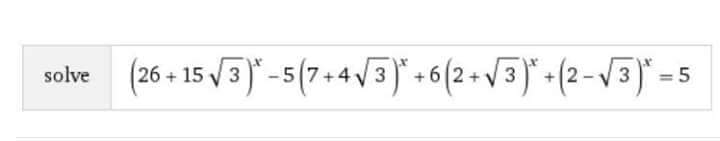
Answered by Rasheed.Sindhi last updated on 23/Jan/18

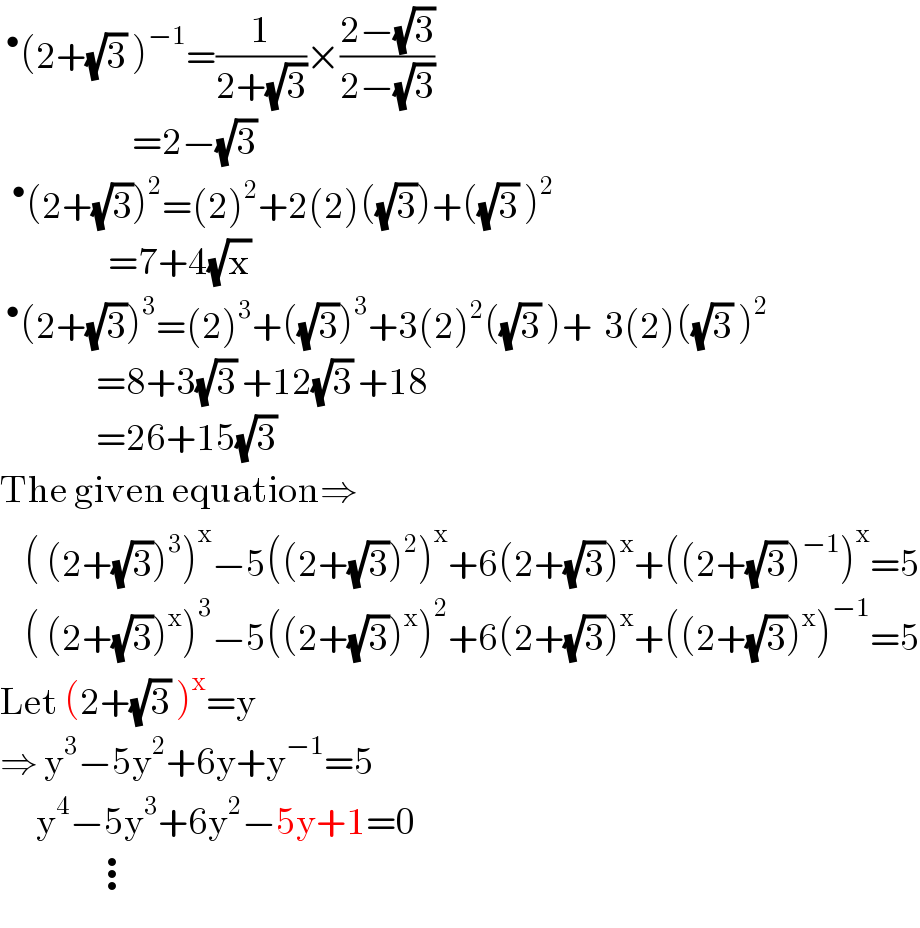
^• (2+(√3) )^(−1) =(1/(2+(√3)))×((2−(√3))/(2−(√3))) =2−(√3) ^• (2+(√3))^2 =(2)^2 +2(2)((√3))+((√3) )^2 =7+4(√x) ^• (2+(√3))^3 =(2)^3 +((√3))^3 +3(2)^2 ((√3) )+ 3(2)((√3) )^2 =8+3(√3) +12(√3) +18 =26+15(√3) The given equation⇒ ( (2+(√3))^3 )^x −5((2+(√3))^2 )^x +6(2+(√3))^x +((2+(√3))^(−1) )^x =5 ( (2+(√3))^x )^3 −5((2+(√3))^x )^2 +6(2+(√3))^x +((2+(√3))^x )^(−1) =5 Let (2+(√3) )^x =y ⇒ y^3 −5y^2 +6y+y^(−1) =5 y^4 −5y^3 +6y^2 −5y+1=0 ⋮

$$\:^{\bullet} \left(\mathrm{2}+\sqrt{\mathrm{3}}\:\right)^{−\mathrm{1}} =\frac{\mathrm{1}}{\mathrm{2}+\sqrt{\mathrm{3}}}×\frac{\mathrm{2}−\sqrt{\mathrm{3}}}{\mathrm{2}−\sqrt{\mathrm{3}}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{2}−\sqrt{\mathrm{3}} \\ $$$$\:\:^{\bullet} \left(\mathrm{2}+\sqrt{\mathrm{3}}\right)^{\mathrm{2}} =\left(\mathrm{2}\right)^{\mathrm{2}} +\mathrm{2}\left(\mathrm{2}\right)\left(\sqrt{\mathrm{3}}\right)+\left(\sqrt{\mathrm{3}}\:\right)^{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{7}+\mathrm{4}\sqrt{\mathrm{x}} \\ $$$$\:^{\bullet} \left(\mathrm{2}+\sqrt{\mathrm{3}}\right)^{\mathrm{3}} =\left(\mathrm{2}\right)^{\mathrm{3}} +\left(\sqrt{\mathrm{3}}\right)^{\mathrm{3}} +\mathrm{3}\left(\mathrm{2}\right)^{\mathrm{2}} \left(\sqrt{\mathrm{3}}\:\right)+\:\:\mathrm{3}\left(\mathrm{2}\right)\left(\sqrt{\mathrm{3}}\:\right)^{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{8}+\mathrm{3}\sqrt{\mathrm{3}}\:+\mathrm{12}\sqrt{\mathrm{3}}\:+\mathrm{18} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{26}+\mathrm{15}\sqrt{\mathrm{3}} \\ $$$$\mathrm{The}\:\mathrm{given}\:\mathrm{equation}\Rightarrow \\ $$$$\:\:\:\:\left(\:\left(\mathrm{2}+\sqrt{\mathrm{3}}\right)^{\mathrm{3}} \right)^{\mathrm{x}} −\mathrm{5}\left(\left(\mathrm{2}+\sqrt{\mathrm{3}}\right)^{\mathrm{2}} \right)^{\mathrm{x}} +\mathrm{6}\left(\mathrm{2}+\sqrt{\mathrm{3}}\right)^{\mathrm{x}} +\left(\left(\mathrm{2}+\sqrt{\mathrm{3}}\right)^{−\mathrm{1}} \right)^{\mathrm{x}} =\mathrm{5} \\ $$$$\:\:\:\:\left(\:\left(\mathrm{2}+\sqrt{\mathrm{3}}\right)^{\mathrm{x}} \right)^{\mathrm{3}} −\mathrm{5}\left(\left(\mathrm{2}+\sqrt{\mathrm{3}}\right)^{\mathrm{x}} \right)^{\mathrm{2}} +\mathrm{6}\left(\mathrm{2}+\sqrt{\mathrm{3}}\right)^{\mathrm{x}} +\left(\left(\mathrm{2}+\sqrt{\mathrm{3}}\right)^{\mathrm{x}} \right)^{−\mathrm{1}} =\mathrm{5} \\ $$$$\mathrm{Let}\:\left(\mathrm{2}+\sqrt{\mathrm{3}}\:\right)^{\mathrm{x}} =\mathrm{y} \\ $$$$\Rightarrow\:\mathrm{y}^{\mathrm{3}} −\mathrm{5y}^{\mathrm{2}} +\mathrm{6y}+\mathrm{y}^{−\mathrm{1}} =\mathrm{5} \\ $$$$\:\:\:\:\:\:\mathrm{y}^{\mathrm{4}} −\mathrm{5y}^{\mathrm{3}} +\mathrm{6y}^{\mathrm{2}} −\mathrm{5y}+\mathrm{1}=\mathrm{0} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\vdots \\ $$

Commented by Rasheed.Sindhi last updated on 23/Jan/18

��şίŕ ţħάήķş ғόŕ ςόŕŕέςţίόή!��

Answered by ajfour last updated on 23/Jan/18

$${x}=\pm\mathrm{1} \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply