Question-28464

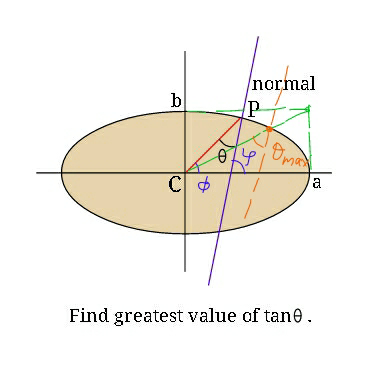
Question Number 28464 by ajfour last updated on 26/Jan/18

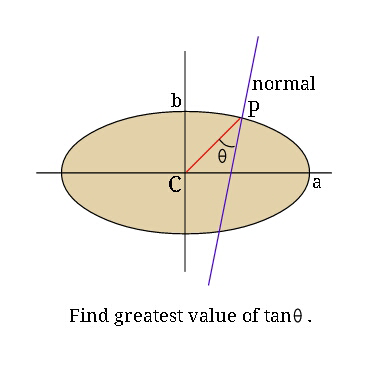
Answered by mrW2 last updated on 26/Jan/18

eqn. of ellipse: (x^2 /a^2 )+(y^2 /b^2 )=1 ((2x)/a^2 )+((2y)/b^2 )×(dy/dx)=0 ⇒(dy/dx)=−(b^2 /a^2 )×(x/y)=inclination of tangent ⇒tan ϕ=inclination of normal=(a^2 /b^2 )×(y/x) (y/x)=tan φ ⇒tan ϕ=(a^2 /b^2 ) tan φ θ=ϕ−φ ⇒tan θ=(((a^2 /b^2 ) tan φ−tan φ)/(1+(a^2 /b^2 ) tan^2 φ))=(((1−(b^2 /a^2 ))tan φ)/((b^2 /a^2 )+tan^2 φ))=(((1−k^2 )tan φ)/(k^2 +tan^2 φ)) with k=(b/a) ⇒tan θ=(((1−k^2 )tan φ)/(k^2 +tan^2 φ))=((1−k^2 )/((k^2 /(tan φ))+tan φ))≤((1−k^2 )/(2(√((k^2 /(tan φ))×tan φ))))=((1−k^2 )/(2k)) i.e. tan θ_(max) =((1−k^2 )/(2k))=((a^2 −b^2 )/(2ab)) or θ_(max) =tan^(−1) ((1−k^2 )/(2k))=tan^(−1) ((a^2 −b^2 )/(2ab)) at (k^2 /(tan φ))=tan φ or φ=±tan^(−1) k=±tan^(−1) (b/a)

$${eqn}.\:{of}\:{ellipse}: \\ $$$$\frac{{x}^{\mathrm{2}} }{{a}^{\mathrm{2}} }+\frac{{y}^{\mathrm{2}} }{{b}^{\mathrm{2}} }=\mathrm{1} \\ $$$$\frac{\mathrm{2}{x}}{{a}^{\mathrm{2}} }+\frac{\mathrm{2}{y}}{{b}^{\mathrm{2}} }×\frac{{dy}}{{dx}}=\mathrm{0} \\ $$$$\Rightarrow\frac{{dy}}{{dx}}=−\frac{{b}^{\mathrm{2}} }{{a}^{\mathrm{2}} }×\frac{{x}}{{y}}={inclination}\:{of}\:{tangent} \\ $$$$\Rightarrow\mathrm{tan}\:\varphi={inclination}\:{of}\:{normal}=\frac{{a}^{\mathrm{2}} }{{b}^{\mathrm{2}} }×\frac{{y}}{{x}} \\ $$$$\frac{{y}}{{x}}=\mathrm{tan}\:\phi \\ $$$$\Rightarrow\mathrm{tan}\:\varphi=\frac{{a}^{\mathrm{2}} }{{b}^{\mathrm{2}} }\:\mathrm{tan}\:\phi \\ $$$$\theta=\varphi−\phi \\ $$$$\Rightarrow\mathrm{tan}\:\theta=\frac{\frac{{a}^{\mathrm{2}} }{{b}^{\mathrm{2}} }\:\mathrm{tan}\:\phi−\mathrm{tan}\:\phi}{\mathrm{1}+\frac{{a}^{\mathrm{2}} }{{b}^{\mathrm{2}} }\:\mathrm{tan}^{\mathrm{2}} \:\phi}=\frac{\left(\mathrm{1}−\frac{{b}^{\mathrm{2}} }{{a}^{\mathrm{2}} }\right)\mathrm{tan}\:\phi}{\frac{{b}^{\mathrm{2}} }{{a}^{\mathrm{2}} }+\mathrm{tan}^{\mathrm{2}} \:\phi}=\frac{\left(\mathrm{1}−{k}^{\mathrm{2}} \right)\mathrm{tan}\:\phi}{{k}^{\mathrm{2}} +\mathrm{tan}^{\mathrm{2}} \:\phi} \\ $$$${with}\:{k}=\frac{{b}}{{a}} \\ $$$$\Rightarrow\mathrm{tan}\:\theta=\frac{\left(\mathrm{1}−{k}^{\mathrm{2}} \right)\mathrm{tan}\:\phi}{{k}^{\mathrm{2}} +\mathrm{tan}^{\mathrm{2}} \:\phi}=\frac{\mathrm{1}−{k}^{\mathrm{2}} }{\frac{{k}^{\mathrm{2}} }{\mathrm{tan}\:\phi}+\mathrm{tan}\:\phi}\leqslant\frac{\mathrm{1}−{k}^{\mathrm{2}} }{\mathrm{2}\sqrt{\frac{{k}^{\mathrm{2}} }{\mathrm{tan}\:\phi}×\mathrm{tan}\:\phi}}=\frac{\mathrm{1}−{k}^{\mathrm{2}} }{\mathrm{2}{k}} \\ $$$${i}.{e}.\:\mathrm{tan}\:\theta_{{max}} =\frac{\mathrm{1}−{k}^{\mathrm{2}} }{\mathrm{2}{k}}=\frac{{a}^{\mathrm{2}} −{b}^{\mathrm{2}} }{\mathrm{2}{ab}} \\ $$$${or}\:\theta_{{max}} =\mathrm{tan}^{−\mathrm{1}} \frac{\mathrm{1}−{k}^{\mathrm{2}} }{\mathrm{2}{k}}=\mathrm{tan}^{−\mathrm{1}} \frac{{a}^{\mathrm{2}} −{b}^{\mathrm{2}} }{\mathrm{2}{ab}} \\ $$$${at}\:\frac{{k}^{\mathrm{2}} }{\mathrm{tan}\:\phi}=\mathrm{tan}\:\phi\:{or}\:\phi=\pm\mathrm{tan}^{−\mathrm{1}} {k}=\pm\mathrm{tan}^{−\mathrm{1}} \frac{{b}}{{a}} \\ $$

Commented by ajfour last updated on 26/Jan/18