Question Number 28467 by Asad8992002 last updated on 26/Jan/18

Commented by abdo imad last updated on 26/Jan/18
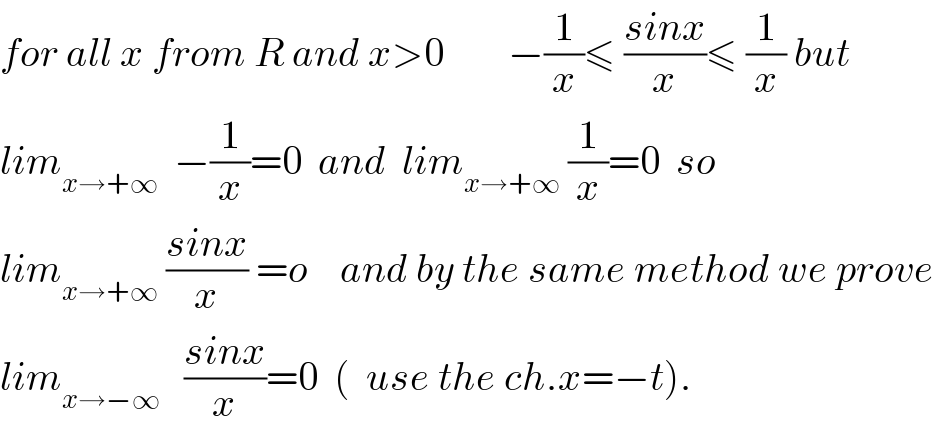
$${for}\:{all}\:{x}\:{from}\:{R}\:{and}\:{x}>\mathrm{0}\:\:\:\:\:\:\:\:−\frac{\mathrm{1}}{{x}}\leqslant\:\frac{{sinx}}{{x}}\leqslant\:\frac{\mathrm{1}}{{x}}\:{but} \\ $$$${lim}_{{x}\rightarrow+\infty} \:\:−\frac{\mathrm{1}}{{x}}=\mathrm{0}\:\:{and}\:\:{lim}_{{x}\rightarrow+\infty} \:\frac{\mathrm{1}}{{x}}=\mathrm{0}\:\:{so} \\ $$$${lim}_{{x}\rightarrow+\infty} \:\frac{{sinx}}{{x}}\:={o}\:\:\:\:{and}\:{by}\:{the}\:{same}\:{method}\:{we}\:{prove} \\ $$$${lim}_{{x}\rightarrow−\infty} \:\:\:\frac{{sinx}}{{x}}=\mathrm{0}\:\:\left(\:\:{use}\:{the}\:{ch}.{x}=−{t}\right). \\ $$
Answered by malwaan last updated on 26/Jan/18

$$\mathrm{zero} \\ $$
Answered by A1B1C1D1 last updated on 26/Jan/18

