Question Number 28480 by naka3546 last updated on 26/Jan/18

Commented by math solver last updated on 29/Jan/18
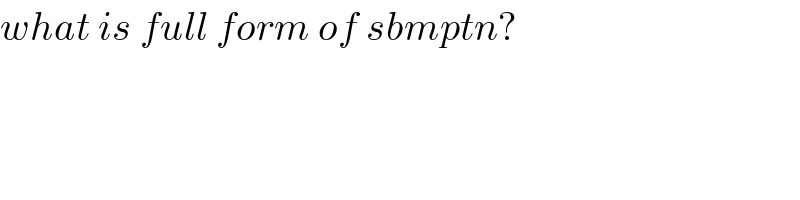
$${what}\:{is}\:{full}\:{form}\:{of}\:{sbmptn}? \\ $$
Answered by ajfour last updated on 26/Jan/18
![lim_(x→∞) [(2^(3x) +3^x )^(1/3) −(2^(2x) −2^x )^(1/2) ] =lim_(x→∞) 2^x {[1+((3/8))^x ]^(1/3) −[1−((1/2))^x ]^(1/2) } =lim_(x→∞) 2^x {1+(1/3)((3/8))^x +...−1+(1/2)((1/2))^x +...} =lim_(x→∞) [((3/4))^x +(1/2)] =(1/2) ⇒ (D).](https://www.tinkutara.com/question/Q28497.png)
$$\underset{{x}\rightarrow\infty} {\mathrm{lim}}\left[\left(\mathrm{2}^{\mathrm{3}{x}} +\mathrm{3}^{{x}} \right)^{\mathrm{1}/\mathrm{3}} −\left(\mathrm{2}^{\mathrm{2}{x}} −\mathrm{2}^{{x}} \right)^{\mathrm{1}/\mathrm{2}} \right] \\ $$$$=\underset{{x}\rightarrow\infty} {\mathrm{lim}2}^{{x}} \left\{\left[\mathrm{1}+\left(\frac{\mathrm{3}}{\mathrm{8}}\right)^{{x}} \right]^{\mathrm{1}/\mathrm{3}} −\left[\mathrm{1}−\left(\frac{\mathrm{1}}{\mathrm{2}}\right)^{{x}} \right]^{\mathrm{1}/\mathrm{2}} \right\} \\ $$$$=\underset{{x}\rightarrow\infty} {\mathrm{lim}2}^{{x}} \left\{\mathrm{1}+\frac{\mathrm{1}}{\mathrm{3}}\left(\frac{\mathrm{3}}{\mathrm{8}}\right)^{{x}} +…−\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{\mathrm{1}}{\mathrm{2}}\right)^{{x}} +…\right\} \\ $$$$=\underset{{x}\rightarrow\infty} {\mathrm{lim}}\left[\left(\frac{\mathrm{3}}{\mathrm{4}}\right)^{{x}} +\frac{\mathrm{1}}{\mathrm{2}}\right]\:=\frac{\mathrm{1}}{\mathrm{2}}\:\:\:\Rightarrow\:\left({D}\right). \\ $$
Commented by naka3546 last updated on 02/Feb/18
![Is it using Taylor Series ? =lim_(x→∞) 2^x {[1+((3/8))^x ]^(1/3) −[1−((1/2))^x ]^(1/2) }](https://www.tinkutara.com/question/Q28970.png)
$${Is}\:{it}\:{using}\:\:{Taylor}\:\:{Series}\:? \\ $$$$=\underset{{x}\rightarrow\infty} {\mathrm{lim}2}^{{x}} \left\{\left[\mathrm{1}+\left(\frac{\mathrm{3}}{\mathrm{8}}\right)^{{x}} \right]^{\mathrm{1}/\mathrm{3}} −\left[\mathrm{1}−\left(\frac{\mathrm{1}}{\mathrm{2}}\right)^{{x}} \right]^{\mathrm{1}/\mathrm{2}} \right\} \\ $$$$ \\ $$
