Question-28501

Question Number 28501 by naka3546 last updated on 26/Jan/18

Commented by naka3546 last updated on 26/Jan/18

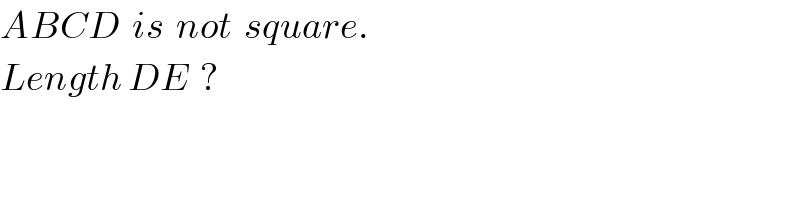
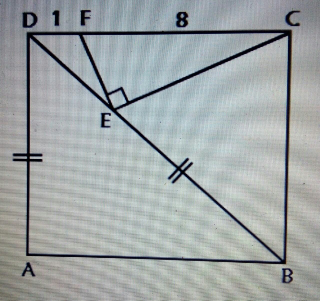
$${ABCD}\:\:{is}\:\:{not}\:\:{square}. \\ $$$${Length}\:{DE}\:\:? \\ $$

Answered by mrW2 last updated on 26/Jan/18

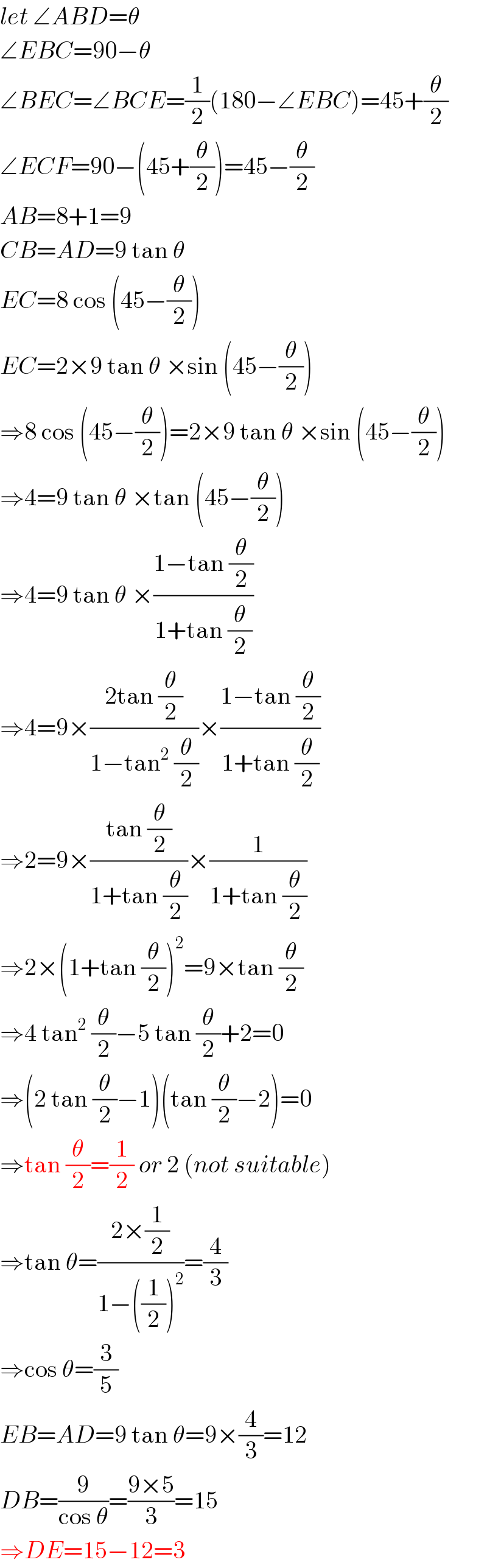
let ∠ABD=θ ∠EBC=90−θ ∠BEC=∠BCE=(1/2)(180−∠EBC)=45+(θ/2) ∠ECF=90−(45+(θ/2))=45−(θ/2) AB=8+1=9 CB=AD=9 tan θ EC=8 cos (45−(θ/2)) EC=2×9 tan θ ×sin (45−(θ/2)) ⇒8 cos (45−(θ/2))=2×9 tan θ ×sin (45−(θ/2)) ⇒4=9 tan θ ×tan (45−(θ/2)) ⇒4=9 tan θ ×((1−tan (θ/2))/(1+tan (θ/2))) ⇒4=9×((2tan (θ/2))/(1−tan^2 (θ/2)))×((1−tan (θ/2))/(1+tan (θ/2))) ⇒2=9×((tan (θ/2))/(1+tan (θ/2)))×(1/(1+tan (θ/2))) ⇒2×(1+tan (θ/2))^2 =9×tan (θ/2) ⇒4 tan^2 (θ/2)−5 tan (θ/2)+2=0 ⇒(2 tan (θ/2)−1)(tan (θ/2)−2)=0 ⇒tan (θ/2)=(1/2) or 2 (not suitable) ⇒tan θ=((2×(1/2))/(1−((1/2))^2 ))=(4/3) ⇒cos θ=(3/5) EB=AD=9 tan θ=9×(4/3)=12 DB=(9/(cos θ))=((9×5)/3)=15 ⇒DE=15−12=3

$${let}\:\angle{ABD}=\theta \\ $$$$\angle{EBC}=\mathrm{90}−\theta \\ $$$$\angle{BEC}=\angle{BCE}=\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{180}−\angle{EBC}\right)=\mathrm{45}+\frac{\theta}{\mathrm{2}} \\ $$$$\angle{ECF}=\mathrm{90}−\left(\mathrm{45}+\frac{\theta}{\mathrm{2}}\right)=\mathrm{45}−\frac{\theta}{\mathrm{2}} \\ $$$${AB}=\mathrm{8}+\mathrm{1}=\mathrm{9} \\ $$$${CB}={AD}=\mathrm{9}\:\mathrm{tan}\:\theta \\ $$$${EC}=\mathrm{8}\:\mathrm{cos}\:\left(\mathrm{45}−\frac{\theta}{\mathrm{2}}\right) \\ $$$${EC}=\mathrm{2}×\mathrm{9}\:\mathrm{tan}\:\theta\:×\mathrm{sin}\:\left(\mathrm{45}−\frac{\theta}{\mathrm{2}}\right) \\ $$$$\Rightarrow\mathrm{8}\:\mathrm{cos}\:\left(\mathrm{45}−\frac{\theta}{\mathrm{2}}\right)=\mathrm{2}×\mathrm{9}\:\mathrm{tan}\:\theta\:×\mathrm{sin}\:\left(\mathrm{45}−\frac{\theta}{\mathrm{2}}\right) \\ $$$$\Rightarrow\mathrm{4}=\mathrm{9}\:\mathrm{tan}\:\theta\:×\mathrm{tan}\:\left(\mathrm{45}−\frac{\theta}{\mathrm{2}}\right) \\ $$$$\Rightarrow\mathrm{4}=\mathrm{9}\:\mathrm{tan}\:\theta\:×\frac{\mathrm{1}−\mathrm{tan}\:\frac{\theta}{\mathrm{2}}}{\mathrm{1}+\mathrm{tan}\:\frac{\theta}{\mathrm{2}}} \\ $$$$\Rightarrow\mathrm{4}=\mathrm{9}×\frac{\mathrm{2tan}\:\frac{\theta}{\mathrm{2}}}{\mathrm{1}−\mathrm{tan}^{\mathrm{2}} \:\frac{\theta}{\mathrm{2}}}×\frac{\mathrm{1}−\mathrm{tan}\:\frac{\theta}{\mathrm{2}}}{\mathrm{1}+\mathrm{tan}\:\frac{\theta}{\mathrm{2}}} \\ $$$$\Rightarrow\mathrm{2}=\mathrm{9}×\frac{\mathrm{tan}\:\frac{\theta}{\mathrm{2}}}{\mathrm{1}+\mathrm{tan}\:\frac{\theta}{\mathrm{2}}}×\frac{\mathrm{1}}{\mathrm{1}+\mathrm{tan}\:\frac{\theta}{\mathrm{2}}} \\ $$$$\Rightarrow\mathrm{2}×\left(\mathrm{1}+\mathrm{tan}\:\frac{\theta}{\mathrm{2}}\right)^{\mathrm{2}} =\mathrm{9}×\mathrm{tan}\:\frac{\theta}{\mathrm{2}} \\ $$$$\Rightarrow\mathrm{4}\:\mathrm{tan}^{\mathrm{2}} \:\frac{\theta}{\mathrm{2}}−\mathrm{5}\:\mathrm{tan}\:\frac{\theta}{\mathrm{2}}+\mathrm{2}=\mathrm{0} \\ $$$$\Rightarrow\left(\mathrm{2}\:\mathrm{tan}\:\frac{\theta}{\mathrm{2}}−\mathrm{1}\right)\left(\mathrm{tan}\:\frac{\theta}{\mathrm{2}}−\mathrm{2}\right)=\mathrm{0} \\ $$$$\Rightarrow\mathrm{tan}\:\frac{\theta}{\mathrm{2}}=\frac{\mathrm{1}}{\mathrm{2}}\:{or}\:\mathrm{2}\:\left({not}\:{suitable}\right) \\ $$$$\Rightarrow\mathrm{tan}\:\theta=\frac{\mathrm{2}×\frac{\mathrm{1}}{\mathrm{2}}}{\mathrm{1}−\left(\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} }=\frac{\mathrm{4}}{\mathrm{3}} \\ $$$$\Rightarrow\mathrm{cos}\:\theta=\frac{\mathrm{3}}{\mathrm{5}} \\ $$$${EB}={AD}=\mathrm{9}\:\mathrm{tan}\:\theta=\mathrm{9}×\frac{\mathrm{4}}{\mathrm{3}}=\mathrm{12} \\ $$$${DB}=\frac{\mathrm{9}}{\mathrm{cos}\:\theta}=\frac{\mathrm{9}×\mathrm{5}}{\mathrm{3}}=\mathrm{15} \\ $$$$\Rightarrow{DE}=\mathrm{15}−\mathrm{12}=\mathrm{3} \\ $$

Answered by ajfour last updated on 26/Jan/18

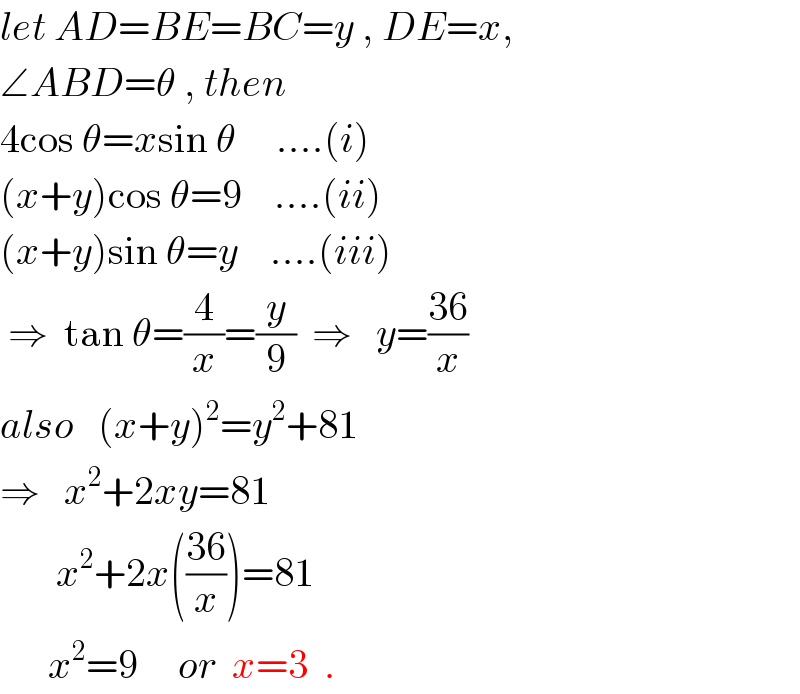
let AD=BE=BC=y , DE=x, ∠ABD=θ , then 4cos θ=xsin θ ....(i) (x+y)cos θ=9 ....(ii) (x+y)sin θ=y ....(iii) ⇒ tan θ=(4/x)=(y/9) ⇒ y=((36)/x) also (x+y)^2 =y^2 +81 ⇒ x^2 +2xy=81 x^2 +2x(((36)/x))=81 x^2 =9 or x=3 .

$${let}\:{AD}={BE}={BC}={y}\:,\:{DE}={x}, \\ $$$$\angle{ABD}=\theta\:,\:{then} \\ $$$$\mathrm{4cos}\:\theta={x}\mathrm{sin}\:\theta\:\:\:\:\:….\left({i}\right) \\ $$$$\left({x}+{y}\right)\mathrm{cos}\:\theta=\mathrm{9}\:\:\:\:….\left({ii}\right) \\ $$$$\left({x}+{y}\right)\mathrm{sin}\:\theta={y}\:\:\:\:….\left({iii}\right) \\ $$$$\:\Rightarrow\:\:\mathrm{tan}\:\theta=\frac{\mathrm{4}}{{x}}=\frac{{y}}{\mathrm{9}}\:\:\Rightarrow\:\:\:{y}=\frac{\mathrm{36}}{{x}} \\ $$$${also}\:\:\:\left({x}+{y}\right)^{\mathrm{2}} ={y}^{\mathrm{2}} +\mathrm{81} \\ $$$$\Rightarrow\:\:\:{x}^{\mathrm{2}} +\mathrm{2}{xy}=\mathrm{81} \\ $$$$\:\:\:\:\:\:\:{x}^{\mathrm{2}} +\mathrm{2}{x}\left(\frac{\mathrm{36}}{{x}}\right)=\mathrm{81} \\ $$$$\:\:\:\:\:\:{x}^{\mathrm{2}} =\mathrm{9}\:\:\:\:\:{or}\:\:{x}=\mathrm{3}\:\:. \\ $$

Commented by mrW2 last updated on 27/Jan/18

$$\mathcal{G}{reat}! \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply