Menu Close

Question-28583

Tinku Tara 0 Comments
Pin




Question Number 28583 by tawa tawa last updated on 27/Jan/18
Commented by tawa tawa last updated on 27/Jan/18
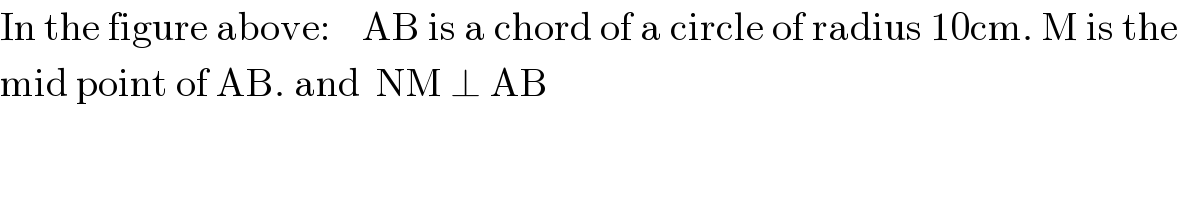
In the figure above: AB is a chord of a circle of radius 10cm. M is the mid point of AB. and NM ⊥ AB
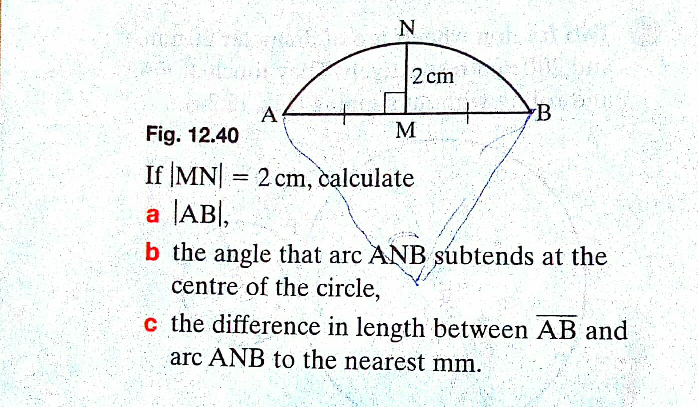
$$\mathrm{In}\:\mathrm{the}\:\mathrm{figure}\:\mathrm{above}:\:\:\:\:\mathrm{AB}\:\mathrm{is}\:\mathrm{a}\:\mathrm{chord}\:\mathrm{of}\:\mathrm{a}\:\mathrm{circle}\:\mathrm{of}\:\mathrm{radius}\:\mathrm{10cm}.\:\mathrm{M}\:\mathrm{is}\:\mathrm{the} \\ $$$$\mathrm{mid}\:\mathrm{point}\:\mathrm{of}\:\mathrm{AB}.\:\mathrm{and}\:\:\mathrm{NM}\:\bot\:\mathrm{AB} \\ $$
Answered by Rasheed.Sindhi last updated on 27/Jan/18
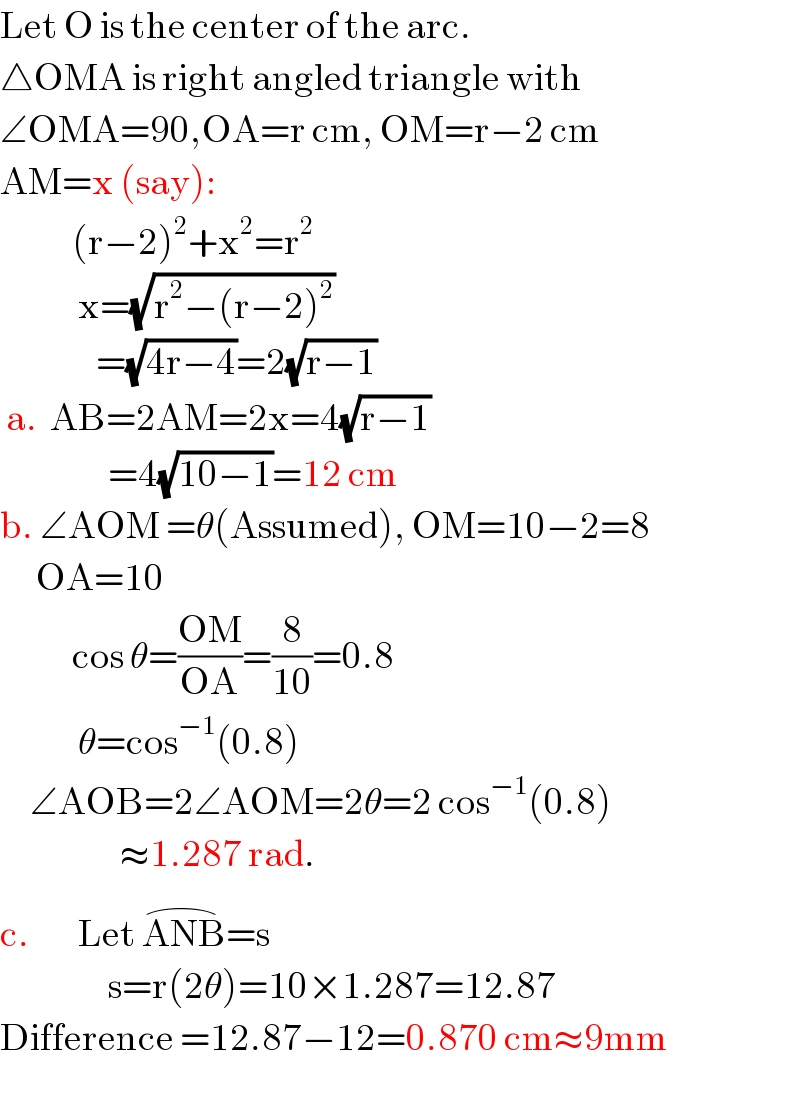
Let O is the center of the arc. △OMA is right angled triangle with ∠OMA=90,OA=r cm, OM=r−2 cm AM=x (say): (r−2)^2 +x^2 =r^2 x=(√(r^2 −(r−2)^2 )) =(√(4r−4))=2(√(r−1)) a. AB=2AM=2x=4(√(r−1)) =4(√(10−1))=12 cm b. ∠AOM =θ(Assumed), OM=10−2=8 OA=10 cos θ=((OM)/(OA))=(8/(10))=0.8 θ=cos^(−1) (0.8) ∠AOB=2∠AOM=2θ=2 cos^(−1) (0.8) ≈1.287 rad. c. Let ANB^(⌢) =s s=r(2θ)=10×1.287=12.87 Difference =12.87−12=0.870 cm≈9mm
$$\mathrm{Let}\:\mathrm{O}\:\mathrm{is}\:\mathrm{the}\:\mathrm{center}\:\mathrm{of}\:\mathrm{the}\:\mathrm{arc}. \\ $$$$\bigtriangleup\mathrm{OMA}\:\mathrm{is}\:\mathrm{right}\:\mathrm{angled}\:\mathrm{triangle}\:\mathrm{with} \\ $$$$\angle\mathrm{OMA}=\mathrm{90},\mathrm{OA}=\mathrm{r}\:\mathrm{cm},\:\mathrm{OM}=\mathrm{r}−\mathrm{2}\:\mathrm{cm} \\ $$$$\mathrm{AM}=\mathrm{x}\:\left(\mathrm{say}\right): \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\left(\mathrm{r}−\mathrm{2}\right)^{\mathrm{2}} +\mathrm{x}^{\mathrm{2}} =\mathrm{r}^{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{x}=\sqrt{\mathrm{r}^{\mathrm{2}} −\left(\mathrm{r}−\mathrm{2}\right)^{\mathrm{2}} } \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\sqrt{\mathrm{4r}−\mathrm{4}}=\mathrm{2}\sqrt{\mathrm{r}−\mathrm{1}} \\ $$$$\:\mathrm{a}.\:\:\mathrm{AB}=\mathrm{2AM}=\mathrm{2x}=\mathrm{4}\sqrt{\mathrm{r}−\mathrm{1}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{4}\sqrt{\mathrm{10}−\mathrm{1}}=\mathrm{12}\:\mathrm{cm} \\ $$$$\mathrm{b}.\:\angle\mathrm{AOM}\:=\theta\left(\mathrm{Assumed}\right),\:\mathrm{OM}=\mathrm{10}−\mathrm{2}=\mathrm{8} \\ $$$$\:\:\:\:\:\:\mathrm{OA}=\mathrm{10} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{cos}\:\theta=\frac{\mathrm{OM}}{\mathrm{OA}}=\frac{\mathrm{8}}{\mathrm{10}}=\mathrm{0}.\mathrm{8} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\theta=\mathrm{cos}^{−\mathrm{1}} \left(\mathrm{0}.\mathrm{8}\right) \\ $$$$\:\:\:\:\:\angle\mathrm{AOB}=\mathrm{2}\angle\mathrm{AOM}=\mathrm{2}\theta=\mathrm{2}\:\mathrm{cos}^{−\mathrm{1}} \left(\mathrm{0}.\mathrm{8}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\approx\mathrm{1}.\mathrm{287}\:\mathrm{rad}. \\ $$$$\mathrm{c}.\:\:\:\:\:\:\:\:\mathrm{Let}\:\overset{\frown} {\mathrm{ANB}}=\mathrm{s} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{s}=\mathrm{r}\left(\mathrm{2}\theta\right)=\mathrm{10}×\mathrm{1}.\mathrm{287}=\mathrm{12}.\mathrm{87} \\ $$$$\mathrm{Difference}\:=\mathrm{12}.\mathrm{87}−\mathrm{12}=\mathrm{0}.\mathrm{870}\:\mathrm{cm}\approx\mathrm{9mm} \\ $$
Commented by tawa tawa last updated on 27/Jan/18
God bless you sir
$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *