Question Number 28597 by beh.i83417@gmail.com last updated on 27/Jan/18

Commented by beh.i83417@gmail.com last updated on 27/Jan/18
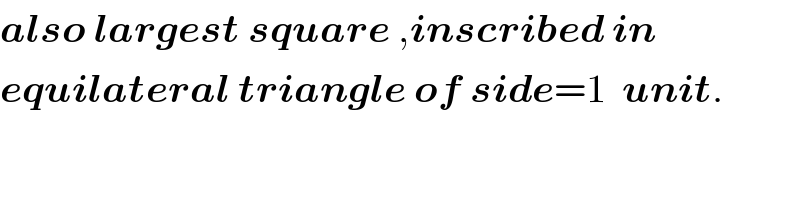
$$\boldsymbol{{also}}\:\boldsymbol{{largest}}\:\boldsymbol{{square}}\:,\boldsymbol{{inscribed}}\:\boldsymbol{{in}} \\ $$$$\boldsymbol{{equilateral}}\:\boldsymbol{{triangle}}\:\boldsymbol{{of}}\:\boldsymbol{{side}}=\mathrm{1}\:\:\boldsymbol{{unit}}. \\ $$
Answered by mrW2 last updated on 29/Jan/18

$${max}.\:{equilateral}\:{triangle}: \\ $$$${a}=\frac{\mathrm{1}}{\mathrm{cos}\:\mathrm{15}°}=\frac{\mathrm{4}}{\:\sqrt{\mathrm{2}}+\sqrt{\mathrm{6}}}=\sqrt{\mathrm{6}}−\sqrt{\mathrm{2}} \\ $$$${A}=\frac{\sqrt{\mathrm{3}}}{\mathrm{4}}{a}^{\mathrm{2}} =\frac{\sqrt{\mathrm{3}}}{\mathrm{4}}\left(\mathrm{8}−\mathrm{4}\sqrt{\mathrm{3}}\right)=\mathrm{2}\sqrt{\mathrm{3}}−\mathrm{3} \\ $$$$ \\ $$$${max}.\:{square}\:{in}\:{equilateral}\:{triangle}: \\ $$$$\frac{{b}}{\mathrm{1}}=\frac{\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}−{b}}{\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}}=\frac{\sqrt{\mathrm{3}}−\mathrm{2}{b}}{\:\sqrt{\mathrm{3}}} \\ $$$$\Rightarrow{b}=\frac{\sqrt{\mathrm{3}}}{\mathrm{2}+\sqrt{\mathrm{3}}}=\mathrm{2}\sqrt{\mathrm{3}}−\mathrm{3} \\ $$$${A}={b}^{\mathrm{2}} =\mathrm{21}−\mathrm{12}\sqrt{\mathrm{3}} \\ $$
