Question Number 28690 by ajfour last updated on 28/Jan/18

Commented by ajfour last updated on 28/Jan/18

$${Find}\:{the}\:{area}\:{in}\:{blue}\:{in}\:{terms}\:{of} \\ $$$$\boldsymbol{{r}}\:{and}\:\boldsymbol{{d}}\:. \\ $$
Commented by beh.i83417@gmail.com last updated on 29/Jan/18
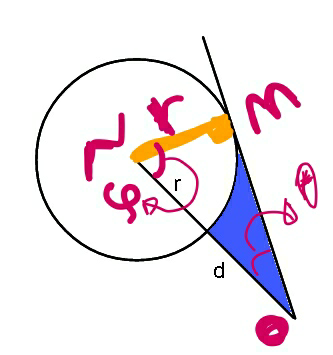
Commented by beh.i83417@gmail.com last updated on 29/Jan/18
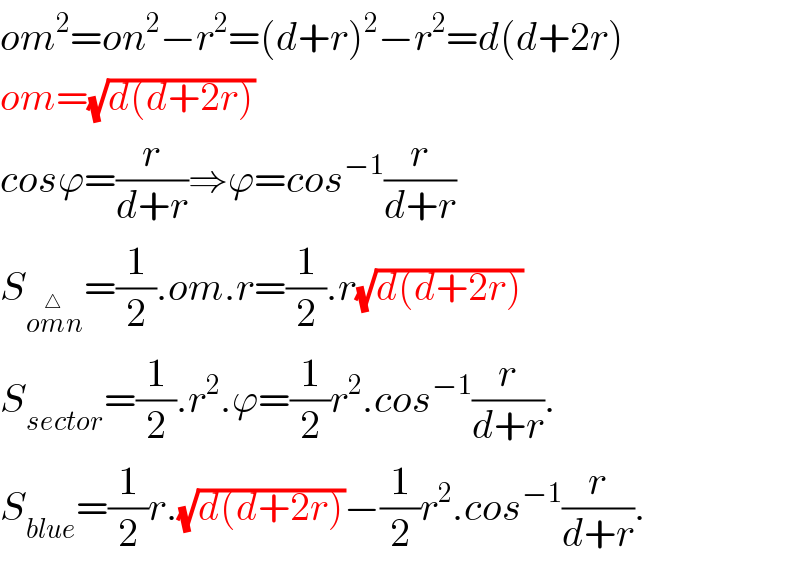
$${om}^{\mathrm{2}} ={on}^{\mathrm{2}} −{r}^{\mathrm{2}} =\left({d}+{r}\right)^{\mathrm{2}} −{r}^{\mathrm{2}} ={d}\left({d}+\mathrm{2}{r}\right) \\ $$$${om}=\sqrt{{d}\left({d}+\mathrm{2}{r}\right)} \\ $$$${cos}\varphi=\frac{{r}}{{d}+{r}}\Rightarrow\varphi={cos}^{−\mathrm{1}} \frac{{r}}{{d}+{r}} \\ $$$${S}_{{o}\overset{\bigtriangleup} {{m}n}} =\frac{\mathrm{1}}{\mathrm{2}}.{om}.{r}=\frac{\mathrm{1}}{\mathrm{2}}.{r}\sqrt{{d}\left({d}+\mathrm{2}{r}\right)} \\ $$$${S}_{{sector}} =\frac{\mathrm{1}}{\mathrm{2}}.{r}^{\mathrm{2}} .\varphi=\frac{\mathrm{1}}{\mathrm{2}}{r}^{\mathrm{2}} .{cos}^{−\mathrm{1}} \frac{{r}}{{d}+{r}}. \\ $$$${S}_{{blue}} =\frac{\mathrm{1}}{\mathrm{2}}{r}.\sqrt{{d}\left({d}+\mathrm{2}{r}\right)}−\frac{\mathrm{1}}{\mathrm{2}}{r}^{\mathrm{2}} .{cos}^{−\mathrm{1}} \frac{{r}}{{d}+{r}}. \\ $$
Commented by beh.i83417@gmail.com last updated on 29/Jan/18
$${thank}\:{you}\:{master}.{corrected}. \\ $$
Commented by ajfour last updated on 29/Jan/18
$${Thanks}\:{for}\:{solving}\:{Sir}. \\ $$
