Menu Close

Question-28762

Tinku Tara 0 Comments
Pin




Question Number 28762 by naka3546 last updated on 30/Jan/18
Commented by naka3546 last updated on 30/Jan/18
PF ?
$${PF}\:\:? \\ $$
Commented by naka3546 last updated on 30/Jan/18
PF ?
$${PF}\:\:? \\ $$
Commented by ajfour last updated on 30/Jan/18
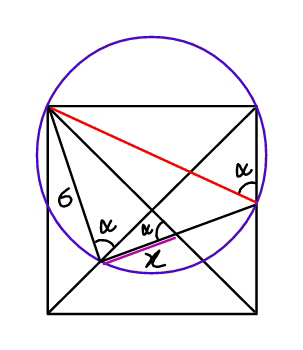
Commented by ajfour last updated on 30/Jan/18
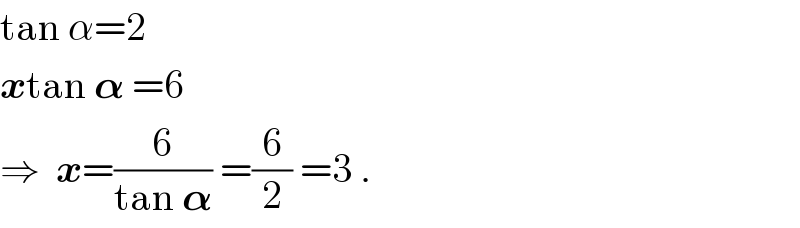
tan α=2 xtan 𝛂 =6 ⇒ x=(6/(tan 𝛂)) =(6/2) =3 .
$$\mathrm{tan}\:\alpha=\mathrm{2} \\ $$$$\boldsymbol{{x}}\mathrm{tan}\:\boldsymbol{\alpha}\:=\mathrm{6} \\ $$$$\Rightarrow\:\:\boldsymbol{{x}}=\frac{\mathrm{6}}{\mathrm{tan}\:\boldsymbol{\alpha}}\:=\frac{\mathrm{6}}{\mathrm{2}}\:=\mathrm{3}\:. \\ $$
Commented by mrW2 last updated on 30/Jan/18
That′s nice!
$${That}'{s}\:{nice}! \\ $$
Commented by ajfour last updated on 30/Jan/18
thanks Sir !
$${thanks}\:{Sir}\:! \\ $$
Answered by mrW2 last updated on 30/Jan/18
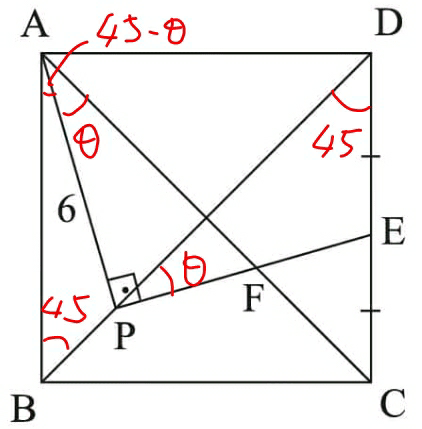
Commented by mrW2 last updated on 30/Jan/18
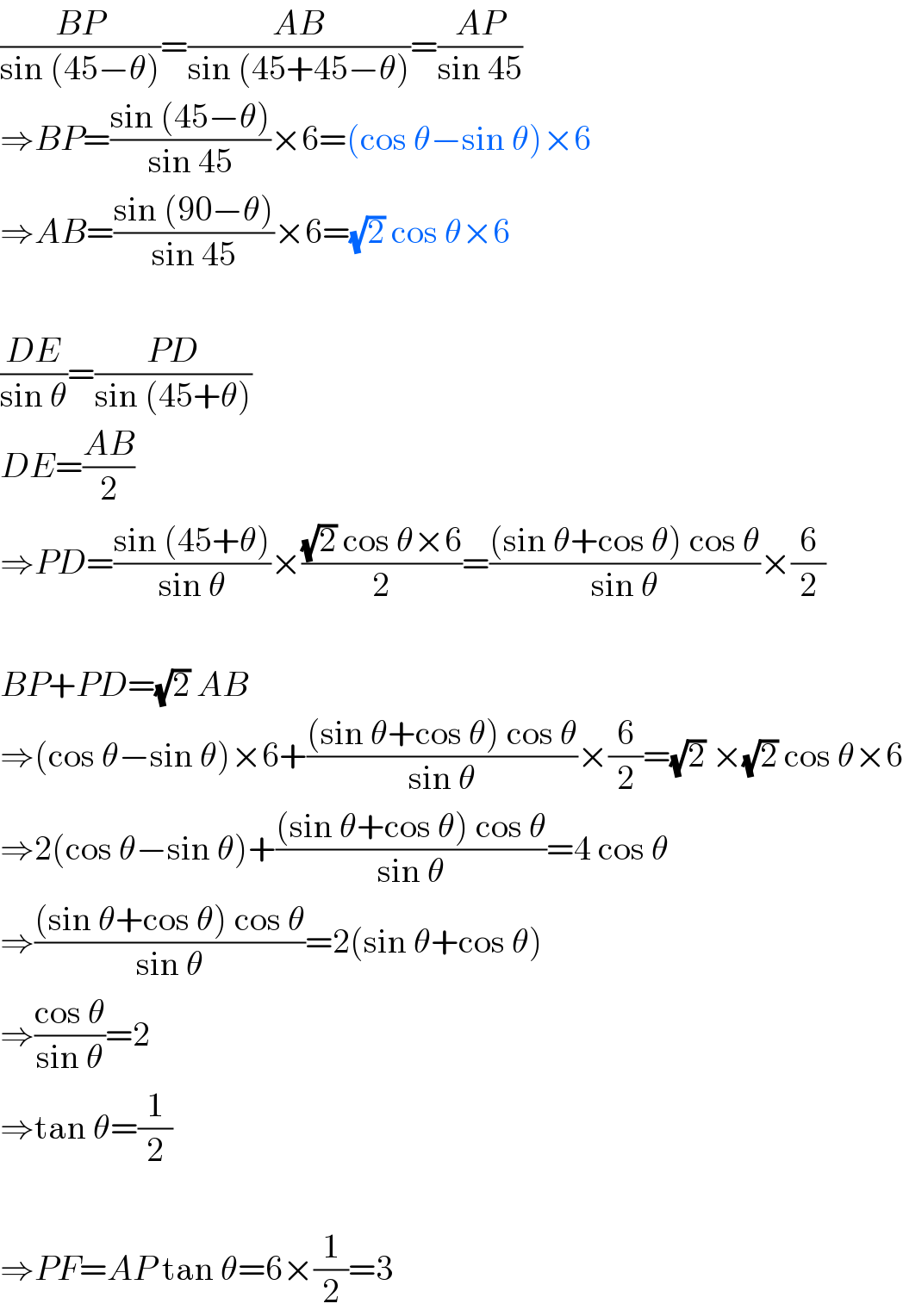
((BP)/(sin (45−θ)))=((AB)/(sin (45+45−θ)))=((AP)/(sin 45)) ⇒BP=((sin (45−θ))/(sin 45))×6=(cos θ−sin θ)×6 ⇒AB=((sin (90−θ))/(sin 45))×6=(√2) cos θ×6 ((DE)/(sin θ))=((PD)/(sin (45+θ))) DE=((AB)/2) ⇒PD=((sin (45+θ))/(sin θ))×(((√2) cos θ×6)/2)=(((sin θ+cos θ) cos θ)/(sin θ))×(6/2) BP+PD=(√2) AB ⇒(cos θ−sin θ)×6+(((sin θ+cos θ) cos θ)/(sin θ))×(6/2)=(√2) ×(√2) cos θ×6 ⇒2(cos θ−sin θ)+(((sin θ+cos θ) cos θ)/(sin θ))=4 cos θ ⇒(((sin θ+cos θ) cos θ)/(sin θ))=2(sin θ+cos θ) ⇒((cos θ)/(sin θ))=2 ⇒tan θ=(1/2) ⇒PF=AP tan θ=6×(1/2)=3
$$\frac{{BP}}{\mathrm{sin}\:\left(\mathrm{45}−\theta\right)}=\frac{{AB}}{\mathrm{sin}\:\left(\mathrm{45}+\mathrm{45}−\theta\right)}=\frac{{AP}}{\mathrm{sin}\:\mathrm{45}} \\ $$$$\Rightarrow{BP}=\frac{\mathrm{sin}\:\left(\mathrm{45}−\theta\right)}{\mathrm{sin}\:\mathrm{45}}×\mathrm{6}=\left(\mathrm{cos}\:\theta−\mathrm{sin}\:\theta\right)×\mathrm{6} \\ $$$$\Rightarrow{AB}=\frac{\mathrm{sin}\:\left(\mathrm{90}−\theta\right)}{\mathrm{sin}\:\mathrm{45}}×\mathrm{6}=\sqrt{\mathrm{2}}\:\mathrm{cos}\:\theta×\mathrm{6} \\ $$$$ \\ $$$$\frac{{DE}}{\mathrm{sin}\:\theta}=\frac{{PD}}{\mathrm{sin}\:\left(\mathrm{45}+\theta\right)} \\ $$$${DE}=\frac{{AB}}{\mathrm{2}} \\ $$$$\Rightarrow{PD}=\frac{\mathrm{sin}\:\left(\mathrm{45}+\theta\right)}{\mathrm{sin}\:\theta}×\frac{\sqrt{\mathrm{2}}\:\mathrm{cos}\:\theta×\mathrm{6}}{\mathrm{2}}=\frac{\left(\mathrm{sin}\:\theta+\mathrm{cos}\:\theta\right)\:\mathrm{cos}\:\theta}{\mathrm{sin}\:\theta}×\frac{\mathrm{6}}{\mathrm{2}} \\ $$$$ \\ $$$${BP}+{PD}=\sqrt{\mathrm{2}}\:{AB} \\ $$$$\Rightarrow\left(\mathrm{cos}\:\theta−\mathrm{sin}\:\theta\right)×\mathrm{6}+\frac{\left(\mathrm{sin}\:\theta+\mathrm{cos}\:\theta\right)\:\mathrm{cos}\:\theta}{\mathrm{sin}\:\theta}×\frac{\mathrm{6}}{\mathrm{2}}=\sqrt{\mathrm{2}}\:×\sqrt{\mathrm{2}}\:\mathrm{cos}\:\theta×\mathrm{6} \\ $$$$\Rightarrow\mathrm{2}\left(\mathrm{cos}\:\theta−\mathrm{sin}\:\theta\right)+\frac{\left(\mathrm{sin}\:\theta+\mathrm{cos}\:\theta\right)\:\mathrm{cos}\:\theta}{\mathrm{sin}\:\theta}=\mathrm{4}\:\mathrm{cos}\:\theta \\ $$$$\Rightarrow\frac{\left(\mathrm{sin}\:\theta+\mathrm{cos}\:\theta\right)\:\mathrm{cos}\:\theta}{\mathrm{sin}\:\theta}=\mathrm{2}\left(\mathrm{sin}\:\theta+\mathrm{cos}\:\theta\right) \\ $$$$\Rightarrow\frac{\mathrm{cos}\:\theta}{\mathrm{sin}\:\theta}=\mathrm{2} \\ $$$$\Rightarrow\mathrm{tan}\:\theta=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$ \\ $$$$\Rightarrow{PF}={AP}\:\mathrm{tan}\:\theta=\mathrm{6}×\frac{\mathrm{1}}{\mathrm{2}}=\mathrm{3} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *