Question Number 28894 by amit96 last updated on 01/Feb/18
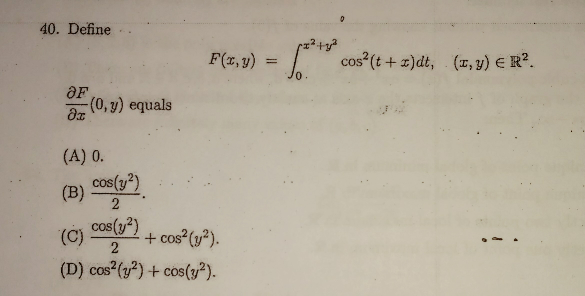
Commented by abdo imad last updated on 01/Feb/18
![let put f(x)=F(x,y)= ∫_0 ^(x^2 +y^2 ) cos^2 (t+x)dt we have by ch. t+x=u ⇒f(x)= ∫_x ^(x^2 +y^2 +x) cos^2 udu =∫_x ^(x^2 +y^2 +x) ((1+cos(2u))/2)du =(1/2)(x^2 +y^2 ) +[(1/4)sin(2u)]_x ^(x^2 +y^2 +x) =(1/2)(x^2 +y^2 ) +(1/4)(sin(2x^2 +2y^2 +2x)−sin(2x)) (∂F/∂x)(x,y)=x +(1/4)( (4x+2)cos(2x^2 +2y^2 +2x)−2cos(2x)) (∂F/∂x)(0,y)= (1/4)( 2cos(2y^2 )−2)=(1/2)cos(2y^2 )−(1/2) and any answer given is correct.!](https://www.tinkutara.com/question/Q28906.png)
$${let}\:{put}\:{f}\left({x}\right)={F}\left({x},{y}\right)=\:\int_{\mathrm{0}} ^{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} } {cos}^{\mathrm{2}} \left({t}+{x}\right){dt}\:\:{we}\:{have}\:{by}\:{ch}. \\ $$$${t}+{x}={u}\:\:\:\:\Rightarrow{f}\left({x}\right)=\:\int_{{x}} ^{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} +{x}} {cos}^{\mathrm{2}} {udu}\:=\int_{{x}} ^{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} +{x}} \:\frac{\mathrm{1}+{cos}\left(\mathrm{2}{u}\right)}{\mathrm{2}}{du} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left({x}^{\mathrm{2}} +{y}^{\mathrm{2}} \right)\:\:+\left[\frac{\mathrm{1}}{\mathrm{4}}{sin}\left(\mathrm{2}{u}\right)\right]_{{x}} ^{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} +{x}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left({x}^{\mathrm{2}} +{y}^{\mathrm{2}} \right)\:+\frac{\mathrm{1}}{\mathrm{4}}\left({sin}\left(\mathrm{2}{x}^{\mathrm{2}} +\mathrm{2}{y}^{\mathrm{2}} +\mathrm{2}{x}\right)−{sin}\left(\mathrm{2}{x}\right)\right) \\ $$$$\frac{\partial{F}}{\partial{x}}\left({x},{y}\right)={x}\:+\frac{\mathrm{1}}{\mathrm{4}}\left(\:\left(\mathrm{4}{x}+\mathrm{2}\right){cos}\left(\mathrm{2}{x}^{\mathrm{2}} +\mathrm{2}{y}^{\mathrm{2}} +\mathrm{2}{x}\right)−\mathrm{2}{cos}\left(\mathrm{2}{x}\right)\right) \\ $$$$\frac{\partial{F}}{\partial{x}}\left(\mathrm{0},{y}\right)=\:\frac{\mathrm{1}}{\mathrm{4}}\left(\:\mathrm{2}{cos}\left(\mathrm{2}{y}^{\mathrm{2}} \right)−\mathrm{2}\right)=\frac{\mathrm{1}}{\mathrm{2}}{cos}\left(\mathrm{2}{y}^{\mathrm{2}} \right)−\frac{\mathrm{1}}{\mathrm{2}}\:{and}\:{any}\:{answer} \\ $$$${given}\:{is}\:{correct}.! \\ $$$$ \\ $$
Commented by abdo imad last updated on 01/Feb/18
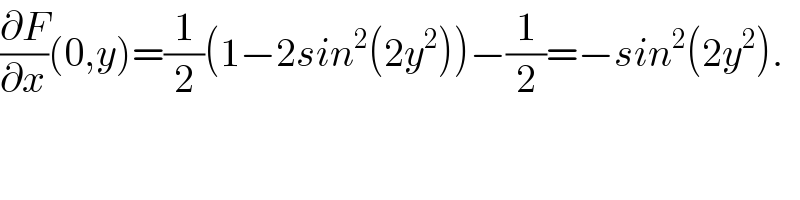
$$\frac{\partial{F}}{\partial{x}}\left(\mathrm{0},{y}\right)=\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{1}−\mathrm{2}{sin}^{\mathrm{2}} \left(\mathrm{2}{y}^{\mathrm{2}} \right)\right)−\frac{\mathrm{1}}{\mathrm{2}}=−{sin}^{\mathrm{2}} \left(\mathrm{2}{y}^{\mathrm{2}} \right). \\ $$
Commented by mrW2 last updated on 01/Feb/18
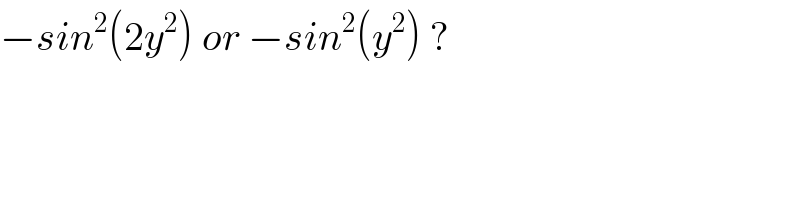
$$−{sin}^{\mathrm{2}} \left(\mathrm{2}{y}^{\mathrm{2}} \right)\:{or}\:−{sin}^{\mathrm{2}} \left({y}^{\mathrm{2}} \right)\:? \\ $$
Commented by amit96 last updated on 01/Feb/18
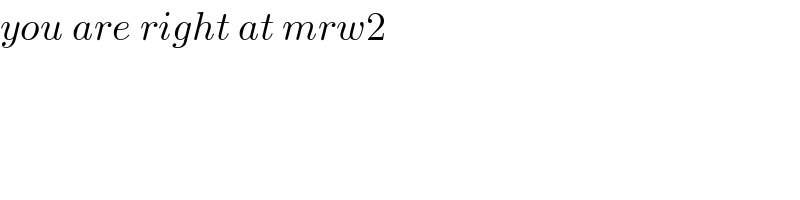
$${you}\:{are}\:{right}\:{at}\:{mrw}\mathrm{2} \\ $$
Commented by mrW2 last updated on 01/Feb/18
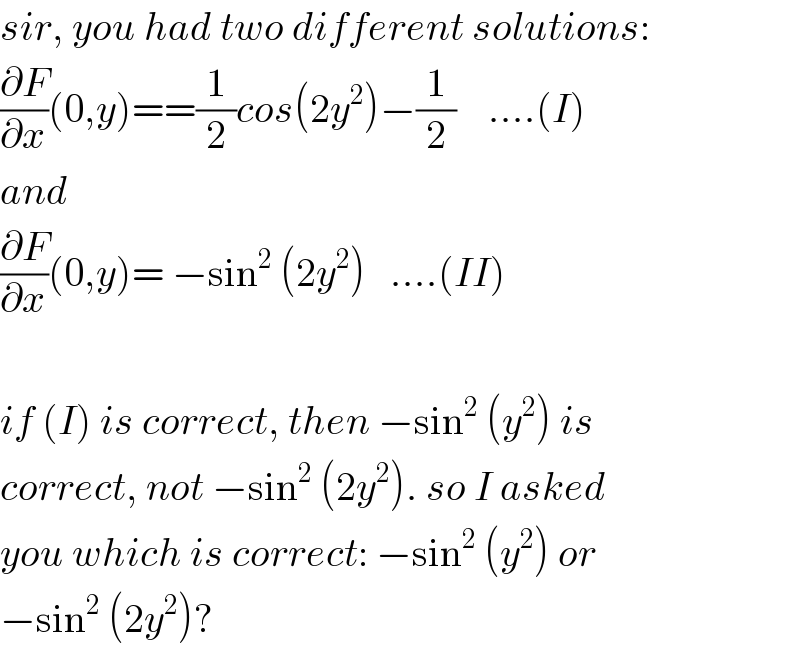
$${sir},\:{you}\:{had}\:{two}\:{different}\:{solutions}: \\ $$$$\frac{\partial{F}}{\partial{x}}\left(\mathrm{0},{y}\right)==\frac{\mathrm{1}}{\mathrm{2}}{cos}\left(\mathrm{2}{y}^{\mathrm{2}} \right)−\frac{\mathrm{1}}{\mathrm{2}}\:\:\:\:….\left({I}\right) \\ $$$${and} \\ $$$$\frac{\partial{F}}{\partial{x}}\left(\mathrm{0},{y}\right)=\:−\mathrm{sin}^{\mathrm{2}} \:\left(\mathrm{2}{y}^{\mathrm{2}} \right)\:\:\:….\left({II}\right) \\ $$$$ \\ $$$${if}\:\left({I}\right)\:{is}\:{correct},\:{then}\:−\mathrm{sin}^{\mathrm{2}} \:\left({y}^{\mathrm{2}} \right)\:{is} \\ $$$${correct},\:{not}\:−\mathrm{sin}^{\mathrm{2}} \:\left(\mathrm{2}{y}^{\mathrm{2}} \right).\:{so}\:{I}\:{asked} \\ $$$${you}\:{which}\:{is}\:{correct}:\:−\mathrm{sin}^{\mathrm{2}} \:\left({y}^{\mathrm{2}} \right)\:{or} \\ $$$$−\mathrm{sin}^{\mathrm{2}} \:\left(\mathrm{2}{y}^{\mathrm{2}} \right)? \\ $$
Answered by mrW2 last updated on 01/Feb/18
![∫cos^2 t dt=(1/2)∫(1+cos 2t)dt=(t/2)+((sin 2t)/4)+C F(x,y)=∫_0 ^( x^2 +y^2 ) cos^2 (t+x)dt =[((t+x)/2)+((sin 2(t+x))/4)]_0 ^(x^2 +y^2 ) =[((x^2 +y^2 +x)/2)−(x/2)+((sin 2(x^2 +y^2 +x))/4)−((sin 2x)/4)] =[((x^2 +y^2 )/2)+((sin 2(x^2 +y^2 +x))/4)−((sin 2x)/4)] (∂F/∂x)=x+((cos 2(x^2 +y^2 +x)×2(2x+1))/4)−((cos 2x)/4)×2 (∂F/∂x)=x+(((2x+1) cos 2(x^2 +y^2 +x))/2)−((cos 2x)/2) (∂F/∂x)(0,y)=((cos 2(y^2 ))/2)−(1/2)=((1−2 sin^2 y^2 )/2)−(1/2)=−sin^2 y^2 ⇒none of the answers is correct.](https://www.tinkutara.com/question/Q28896.png)
$$\int\mathrm{cos}^{\mathrm{2}} \:{t}\:{dt}=\frac{\mathrm{1}}{\mathrm{2}}\int\left(\mathrm{1}+\mathrm{cos}\:\mathrm{2}{t}\right){dt}=\frac{{t}}{\mathrm{2}}+\frac{\mathrm{sin}\:\mathrm{2}{t}}{\mathrm{4}}+{C} \\ $$$${F}\left({x},{y}\right)=\int_{\mathrm{0}} ^{\:{x}^{\mathrm{2}} +{y}^{\mathrm{2}} } \mathrm{cos}^{\mathrm{2}} \:\left({t}+{x}\right){dt} \\ $$$$=\left[\frac{{t}+{x}}{\mathrm{2}}+\frac{\mathrm{sin}\:\mathrm{2}\left({t}+{x}\right)}{\mathrm{4}}\right]_{\mathrm{0}} ^{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} } \\ $$$$=\left[\frac{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} +{x}}{\mathrm{2}}−\frac{{x}}{\mathrm{2}}+\frac{\mathrm{sin}\:\mathrm{2}\left({x}^{\mathrm{2}} +{y}^{\mathrm{2}} +{x}\right)}{\mathrm{4}}−\frac{\mathrm{sin}\:\mathrm{2}{x}}{\mathrm{4}}\right] \\ $$$$=\left[\frac{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} }{\mathrm{2}}+\frac{\mathrm{sin}\:\mathrm{2}\left({x}^{\mathrm{2}} +{y}^{\mathrm{2}} +{x}\right)}{\mathrm{4}}−\frac{\mathrm{sin}\:\mathrm{2}{x}}{\mathrm{4}}\right] \\ $$$$\frac{\partial{F}}{\partial{x}}={x}+\frac{\mathrm{cos}\:\mathrm{2}\left({x}^{\mathrm{2}} +{y}^{\mathrm{2}} +{x}\right)×\mathrm{2}\left(\mathrm{2}{x}+\mathrm{1}\right)}{\mathrm{4}}−\frac{\mathrm{cos}\:\mathrm{2}{x}}{\mathrm{4}}×\mathrm{2} \\ $$$$\frac{\partial{F}}{\partial{x}}={x}+\frac{\left(\mathrm{2}{x}+\mathrm{1}\right)\:\mathrm{cos}\:\mathrm{2}\left({x}^{\mathrm{2}} +{y}^{\mathrm{2}} +{x}\right)}{\mathrm{2}}−\frac{\mathrm{cos}\:\mathrm{2}{x}}{\mathrm{2}} \\ $$$$\frac{\partial{F}}{\partial{x}}\left(\mathrm{0},{y}\right)=\frac{\mathrm{cos}\:\mathrm{2}\left({y}^{\mathrm{2}} \right)}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{2}}=\frac{\mathrm{1}−\mathrm{2}\:\mathrm{sin}^{\mathrm{2}} \:{y}^{\mathrm{2}} }{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{2}}=−\mathrm{sin}^{\mathrm{2}} \:{y}^{\mathrm{2}} \\ $$$$\Rightarrow{none}\:{of}\:{the}\:{answers}\:{is}\:{correct}. \\ $$
Commented by amit96 last updated on 01/Feb/18

$${thanks} \\ $$$$ \\ $$
