Question Number 28960 by Tinkutara last updated on 02/Feb/18

Commented by Tinkutara last updated on 02/Feb/18
Identify if the Statement 2 is true or false and give reasons.
Answered by ajfour last updated on 02/Feb/18
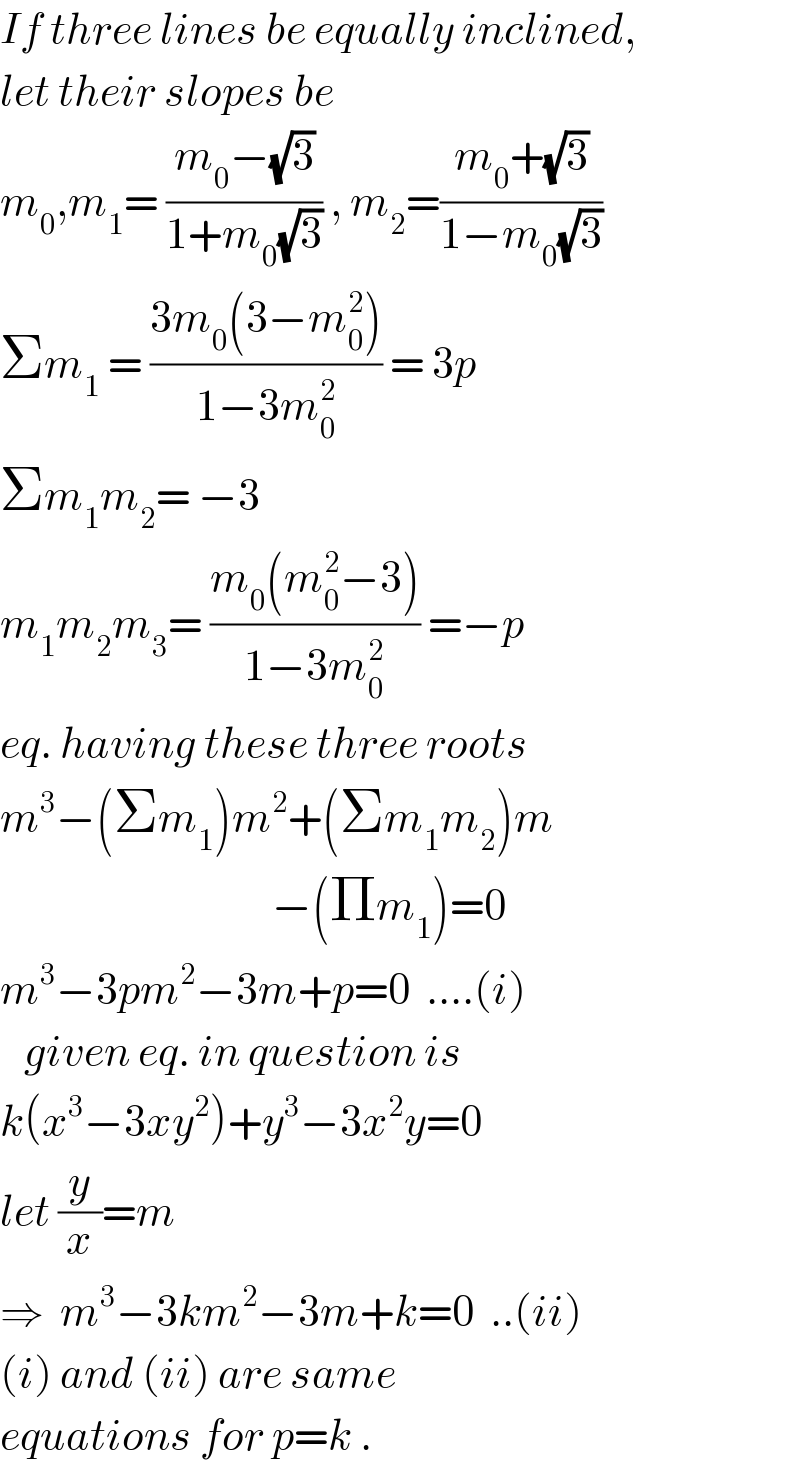
$${If}\:{three}\:{lines}\:{be}\:{equally}\:{inclined}, \\ $$$${let}\:{their}\:{slopes}\:{be}\: \\ $$$${m}_{\mathrm{0}} ,{m}_{\mathrm{1}} =\:\frac{{m}_{\mathrm{0}} −\sqrt{\mathrm{3}}}{\mathrm{1}+{m}_{\mathrm{0}} \sqrt{\mathrm{3}}}\:,\:{m}_{\mathrm{2}} =\frac{{m}_{\mathrm{0}} +\sqrt{\mathrm{3}}}{\mathrm{1}−{m}_{\mathrm{0}} \sqrt{\mathrm{3}}} \\ $$$$\Sigma{m}_{\mathrm{1}} \:=\:\frac{\mathrm{3}{m}_{\mathrm{0}} \left(\mathrm{3}−{m}_{\mathrm{0}} ^{\mathrm{2}} \right)}{\mathrm{1}−\mathrm{3}{m}_{\mathrm{0}} ^{\mathrm{2}} }\:=\:\mathrm{3}{p}\: \\ $$$$\Sigma{m}_{\mathrm{1}} {m}_{\mathrm{2}} =\:−\mathrm{3} \\ $$$${m}_{\mathrm{1}} {m}_{\mathrm{2}} {m}_{\mathrm{3}} =\:\frac{{m}_{\mathrm{0}} \left({m}_{\mathrm{0}} ^{\mathrm{2}} −\mathrm{3}\right)}{\mathrm{1}−\mathrm{3}{m}_{\mathrm{0}} ^{\mathrm{2}} }\:=−{p} \\ $$$${eq}.\:{having}\:{these}\:{three}\:{roots} \\ $$$${m}^{\mathrm{3}} −\left(\Sigma{m}_{\mathrm{1}} \right){m}^{\mathrm{2}} +\left(\Sigma{m}_{\mathrm{1}} {m}_{\mathrm{2}} \right){m} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:−\left(\Pi{m}_{\mathrm{1}} \right)=\mathrm{0} \\ $$$${m}^{\mathrm{3}} −\mathrm{3}{pm}^{\mathrm{2}} −\mathrm{3}{m}+{p}=\mathrm{0}\:\:….\left({i}\right) \\ $$$$\:\:\:{given}\:{eq}.\:{in}\:{question}\:{is} \\ $$$${k}\left({x}^{\mathrm{3}} −\mathrm{3}{xy}^{\mathrm{2}} \right)+{y}^{\mathrm{3}} −\mathrm{3}{x}^{\mathrm{2}} {y}=\mathrm{0} \\ $$$${let}\:\frac{{y}}{{x}}={m} \\ $$$$\Rightarrow\:\:{m}^{\mathrm{3}} −\mathrm{3}{km}^{\mathrm{2}} −\mathrm{3}{m}+{k}=\mathrm{0}\:\:..\left({ii}\right) \\ $$$$\left({i}\right)\:{and}\:\left({ii}\right)\:{are}\:{same} \\ $$$${equations}\:{for}\:{p}={k}\:. \\ $$
Commented by Tinkutara last updated on 03/Feb/18
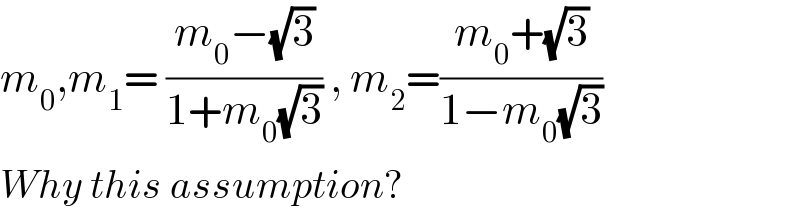
$${m}_{\mathrm{0}} ,{m}_{\mathrm{1}} =\:\frac{{m}_{\mathrm{0}} −\sqrt{\mathrm{3}}}{\mathrm{1}+{m}_{\mathrm{0}} \sqrt{\mathrm{3}}}\:,\:{m}_{\mathrm{2}} =\frac{{m}_{\mathrm{0}} +\sqrt{\mathrm{3}}}{\mathrm{1}−{m}_{\mathrm{0}} \sqrt{\mathrm{3}}} \\ $$$${Why}\:{this}\:{assumption}? \\ $$
Commented by ajfour last updated on 03/Feb/18

$${See}\:{Q}.\mathrm{29007} \\ $$
Commented by Tinkutara last updated on 03/Feb/18
But isn't that means the three lines are equally inclined to one another? We are not given to which line they are inclined.
Commented by ajfour last updated on 03/Feb/18

$${to}\:{each}\:{other},\:{pair}\:{wise}\:{this}\:{can} \\ $$$${be}\:{the}\:{obvious}\:{interpretation}; \\ $$$${means}\:{angles}\:{of}\:{inclination}\:{to} \\ $$$${each}\:{other}\:{is}\:\mathrm{120}°\:,\:{equivalently} \\ $$$$\mathrm{60}°\:{even}. \\ $$
Commented by Tinkutara last updated on 04/Feb/18
Thank you very much Sir! I got the answer.
