Question Number 29048 by $@ty@m last updated on 03/Feb/18

Commented by ajfour last updated on 04/Feb/18
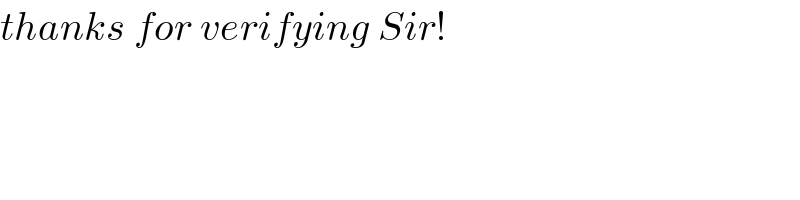
$${thanks}\:{for}\:{verifying}\:{Sir}! \\ $$
Commented by $@ty@m last updated on 04/Feb/18

$${Sorry} \\ $$$${I}\:{dont}\:{have}\:{the}\:{answer}. \\ $$
Commented by ajfour last updated on 04/Feb/18

$${please}\:{explain}\:{Sir}! \\ $$$${i}\:{think}\:{something}\:{wrong}\:{with} \\ $$$${question}.. \\ $$
Commented by ajfour last updated on 04/Feb/18

$${S}_{\mathrm{1}} ={S}_{\mathrm{2}} \:={A}\:\:\:\:\left({say}\right) \\ $$$${S}_{\mathrm{1}} +{S}_{\mathrm{2}} ={S}_{\mathrm{3}} +{S}_{\mathrm{4}} \:=\:\mathrm{2}{A}\:\:\:\:…\left({i}\right) \\ $$$$\mathrm{3}\left({S}_{\mathrm{1}} +{S}_{\mathrm{3}} \right)={S}_{\mathrm{2}} +{S}_{\mathrm{4}} \\ $$$$\Rightarrow\:\:\:\mathrm{3}{A}+\mathrm{3}{S}_{\mathrm{3}} ={A}+{S}_{\mathrm{4}} \\ $$$$\Rightarrow\:\:\:\:\mathrm{3}{S}_{\mathrm{3}} +\mathrm{2}{A}={S}_{\mathrm{4}} \\ $$$${using}\:\left({i}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\mathrm{3}{S}_{\mathrm{3}} +{S}_{\mathrm{3}} +{S}_{\mathrm{4}} ={S}_{\mathrm{4}} \\ $$$$\Rightarrow\:\:\:\:\:\:\:{S}_{\mathrm{3}} =\mathrm{0}\:\:\:. \\ $$$$\Rightarrow\:\:\:\:\:{OD}\:=\mathrm{0}\:. \\ $$$${wrong}\:{data}\:{in}\:{question}\:! \\ $$
Commented by ajfour last updated on 04/Feb/18

Commented by NECx last updated on 03/Feb/18

$${satyam}……\:{ive}\:{not}\:{seen}\:{you} \\ $$$${online}\:{for}\:{a}\:{long}\:{while}.\:{It}\:{feels} \\ $$$${cool}\:{to}\:{see}\:{you}\:\:{back}\:{here}\:{on}\:{the} \\ $$$${forum}. \\ $$
Commented by $@ty@m last updated on 03/Feb/18

$${I}\:{open}\:{this}\:{app}\:{everyday}\:{but} \\ $$$${most}\:{of}\:{the}\:{times}\:{I}\:{fail}\:{to}\:{solve}\: \\ $$$${the}\:{prooblems}. \\ $$$${However}\:{I}\:{am}\:{learning}\:{a}\:{lot}\:{on} \\ $$$${this}\:{platform}. \\ $$
Commented by $@ty@m last updated on 03/Feb/18

$${in}\:{which}\:{class}\:{text}\:{book}\: \\ $$$${can}\:{i}\:{find}\:{this}\:{theorem}? \\ $$
Commented by $@ty@m last updated on 03/Feb/18

Commented by $@ty@m last updated on 03/Feb/18

$${is}\:{it}\:{okay}\:{now}? \\ $$
Commented by Tinkutara last updated on 03/Feb/18
BF=3.
This is direct application of Ceva's Theorem.
Commented by Tinkutara last updated on 03/Feb/18
OD=4
Commented by Tinkutara last updated on 03/Feb/18

Commented by $@ty@m last updated on 03/Feb/18

$${Thanks}\:{a}\:{lot}. \\ $$
Commented by Tinkutara last updated on 03/Feb/18
http://ibb.co/keD4G6
Commented by Tinkutara last updated on 04/Feb/18
OD=3 or 4? What is the answer? I am getting two different answers.
Commented by Tinkutara last updated on 04/Feb/18
This way it comes 3.
Commented by Tinkutara last updated on 04/Feb/18

Commented by mrW2 last updated on 04/Feb/18

$${you}\:{are}\:{right}\:{sir}. \\ $$$${Following}\:{relations}\:{are}\:{valid}: \\ $$$${DC}=\mathrm{2}{BD} \\ $$$${AF}=\mathrm{2}{BF} \\ $$$${AO}=\mathrm{3}{OD} \\ $$
Answered by mrW2 last updated on 04/Feb/18

Commented by mrW2 last updated on 04/Feb/18
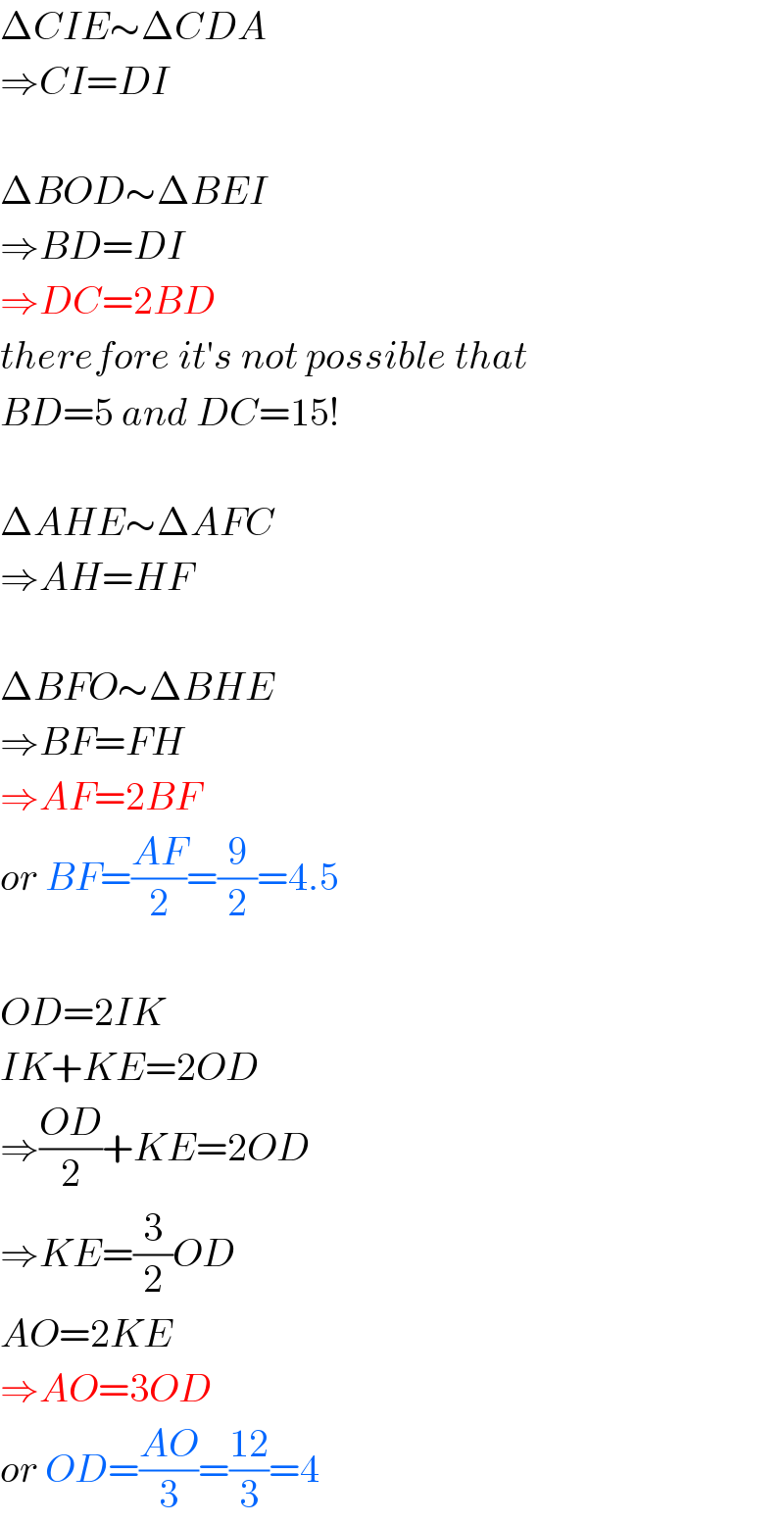
$$\Delta{CIE}\sim\Delta{CDA} \\ $$$$\Rightarrow{CI}={DI} \\ $$$$ \\ $$$$\Delta{BOD}\sim\Delta{BEI} \\ $$$$\Rightarrow{BD}={DI} \\ $$$$\Rightarrow{DC}=\mathrm{2}{BD} \\ $$$${therefore}\:{it}'{s}\:{not}\:{possible}\:{that} \\ $$$${BD}=\mathrm{5}\:{and}\:{DC}=\mathrm{15}! \\ $$$$ \\ $$$$\Delta{AHE}\sim\Delta{AFC} \\ $$$$\Rightarrow{AH}={HF} \\ $$$$ \\ $$$$\Delta{BFO}\sim\Delta{BHE} \\ $$$$\Rightarrow{BF}={FH} \\ $$$$\Rightarrow{AF}=\mathrm{2}{BF} \\ $$$${or}\:{BF}=\frac{{AF}}{\mathrm{2}}=\frac{\mathrm{9}}{\mathrm{2}}=\mathrm{4}.\mathrm{5} \\ $$$$ \\ $$$${OD}=\mathrm{2}{IK} \\ $$$${IK}+{KE}=\mathrm{2}{OD} \\ $$$$\Rightarrow\frac{{OD}}{\mathrm{2}}+{KE}=\mathrm{2}{OD} \\ $$$$\Rightarrow{KE}=\frac{\mathrm{3}}{\mathrm{2}}{OD} \\ $$$${AO}=\mathrm{2}{KE} \\ $$$$\Rightarrow{AO}=\mathrm{3}{OD} \\ $$$${or}\:{OD}=\frac{{AO}}{\mathrm{3}}=\frac{\mathrm{12}}{\mathrm{3}}=\mathrm{4} \\ $$
