Question Number 29107 by ajfour last updated on 04/Feb/18
Commented by ajfour last updated on 04/Feb/18
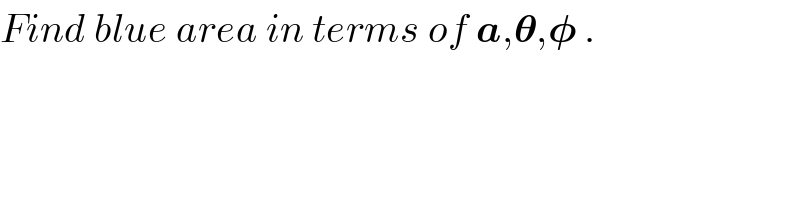
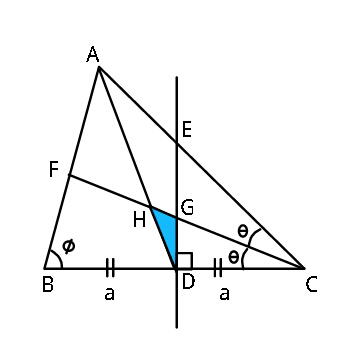
$${Find}\:{blue}\:{area}\:{in}\:{terms}\:{of}\:\boldsymbol{{a}},\boldsymbol{\theta},\boldsymbol{\phi}\:. \\ $$
Answered by mrW2 last updated on 04/Feb/18
![let′s take D as origin and DC as x−axis. y_G =a tan θ (y_F /(tan φ))+(y_F /(tan θ))=2a ⇒y_F =((2a)/((1/(tan φ))+(1/(tan θ))))=((2a)/(((cos φ)/(sin φ))+((cos θ)/(sin θ))))=((2a sin φ sin θ)/(sin (φ+θ))) ⇒x_F =a−(y_F /(tan θ))=a−((2a sin φ cos θ)/(sin (φ+θ)))=−((a sin (φ−θ))/(sin (φ+θ))) similarly, ⇒y_A =((2a sin φ sin 2θ)/(sin (φ+2θ))) ⇒x_A =−((a sin (φ−2θ))/(sin (φ+2θ))) Eqn. of CF: (y/(x−a))=−tan θ ⇒y+tan θ x=a tan θ Eqn. of DA: (y/x)=(((2a sin φ sin 2θ)/(sin (φ+2θ)))/(−((a sin (φ−2θ))/(sin (φ+2θ)))))=−((2 sin φ sin 2θ)/(sin (φ−2θ))) ⇒y=−((2 sin φ sin 2θ)/(sin (φ−2θ)))x ⇒[−((2 sin φ sin 2θ)/(sin (φ−2θ)))+tan θ]x_H =a tan θ ⇒x_H =−((a tan θ)/(((2 sin φ sin 2θ)/(sin (φ−2θ)))−tan θ)) ⇒x_H =−(a/(((4 sin φ cos^2 θ)/(sin (φ−2θ)))−1)) A_(Blue) =(1/2)y_D ∣x_H ∣=(a^2 /2)×((tan θ)/(((4 sin φ cos^2 θ)/(sin (φ−2θ)))−1)) ⇒A_(Blue) =(a^2 /2)×((sin (φ−2θ) tan θ)/(2sin φ +sin (φ+2θ)))](https://www.tinkutara.com/question/Q29112.png)
$${let}'{s}\:{take}\:{D}\:{as}\:{origin}\:{and}\:{DC}\:{as}\:{x}−{axis}. \\ $$$${y}_{{G}} ={a}\:\mathrm{tan}\:\theta \\ $$$$\frac{{y}_{{F}} }{\mathrm{tan}\:\phi}+\frac{{y}_{{F}} }{\mathrm{tan}\:\theta}=\mathrm{2}{a} \\ $$$$\Rightarrow{y}_{{F}} =\frac{\mathrm{2}{a}}{\frac{\mathrm{1}}{\mathrm{tan}\:\phi}+\frac{\mathrm{1}}{\mathrm{tan}\:\theta}}=\frac{\mathrm{2}{a}}{\frac{\mathrm{cos}\:\phi}{\mathrm{sin}\:\phi}+\frac{\mathrm{cos}\:\theta}{\mathrm{sin}\:\theta}}=\frac{\mathrm{2}{a}\:\mathrm{sin}\:\phi\:\mathrm{sin}\:\theta}{\mathrm{sin}\:\left(\phi+\theta\right)} \\ $$$$\Rightarrow{x}_{{F}} ={a}−\frac{{y}_{{F}} }{\mathrm{tan}\:\theta}={a}−\frac{\mathrm{2}{a}\:\mathrm{sin}\:\phi\:\mathrm{cos}\:\theta}{\mathrm{sin}\:\left(\phi+\theta\right)}=−\frac{{a}\:\mathrm{sin}\:\left(\phi−\theta\right)}{\mathrm{sin}\:\left(\phi+\theta\right)} \\ $$$$ \\ $$$${similarly}, \\ $$$$\Rightarrow{y}_{{A}} =\frac{\mathrm{2}{a}\:\mathrm{sin}\:\phi\:\mathrm{sin}\:\mathrm{2}\theta}{\mathrm{sin}\:\left(\phi+\mathrm{2}\theta\right)} \\ $$$$\Rightarrow{x}_{{A}} =−\frac{{a}\:\mathrm{sin}\:\left(\phi−\mathrm{2}\theta\right)}{\mathrm{sin}\:\left(\phi+\mathrm{2}\theta\right)} \\ $$$$ \\ $$$${Eqn}.\:{of}\:{CF}: \\ $$$$\frac{{y}}{{x}−{a}}=−\mathrm{tan}\:\theta \\ $$$$\Rightarrow{y}+\mathrm{tan}\:\theta\:{x}={a}\:\mathrm{tan}\:\theta \\ $$$$ \\ $$$${Eqn}.\:{of}\:{DA}: \\ $$$$\frac{{y}}{{x}}=\frac{\frac{\mathrm{2}{a}\:\mathrm{sin}\:\phi\:\mathrm{sin}\:\mathrm{2}\theta}{\mathrm{sin}\:\left(\phi+\mathrm{2}\theta\right)}}{−\frac{{a}\:\mathrm{sin}\:\left(\phi−\mathrm{2}\theta\right)}{\mathrm{sin}\:\left(\phi+\mathrm{2}\theta\right)}}=−\frac{\mathrm{2}\:\mathrm{sin}\:\phi\:\mathrm{sin}\:\mathrm{2}\theta}{\mathrm{sin}\:\left(\phi−\mathrm{2}\theta\right)} \\ $$$$\Rightarrow{y}=−\frac{\mathrm{2}\:\mathrm{sin}\:\phi\:\mathrm{sin}\:\mathrm{2}\theta}{\mathrm{sin}\:\left(\phi−\mathrm{2}\theta\right)}{x} \\ $$$$ \\ $$$$\Rightarrow\left[−\frac{\mathrm{2}\:\mathrm{sin}\:\phi\:\mathrm{sin}\:\mathrm{2}\theta}{\mathrm{sin}\:\left(\phi−\mathrm{2}\theta\right)}+\mathrm{tan}\:\theta\right]{x}_{{H}} ={a}\:\mathrm{tan}\:\theta \\ $$$$\Rightarrow{x}_{{H}} =−\frac{{a}\:\mathrm{tan}\:\theta}{\frac{\mathrm{2}\:\mathrm{sin}\:\phi\:\mathrm{sin}\:\mathrm{2}\theta}{\mathrm{sin}\:\left(\phi−\mathrm{2}\theta\right)}−\mathrm{tan}\:\theta} \\ $$$$\Rightarrow{x}_{{H}} =−\frac{{a}}{\frac{\mathrm{4}\:\mathrm{sin}\:\phi\:\mathrm{cos}^{\mathrm{2}} \:\theta}{\mathrm{sin}\:\left(\phi−\mathrm{2}\theta\right)}−\mathrm{1}} \\ $$$$ \\ $$$${A}_{{Blue}} =\frac{\mathrm{1}}{\mathrm{2}}{y}_{{D}} \mid{x}_{{H}} \mid=\frac{{a}^{\mathrm{2}} }{\mathrm{2}}×\frac{\mathrm{tan}\:\theta}{\frac{\mathrm{4}\:\mathrm{sin}\:\phi\:\mathrm{cos}^{\mathrm{2}} \:\theta}{\mathrm{sin}\:\left(\phi−\mathrm{2}\theta\right)}−\mathrm{1}} \\ $$$$\Rightarrow{A}_{{Blue}} =\frac{{a}^{\mathrm{2}} }{\mathrm{2}}×\frac{\mathrm{sin}\:\left(\phi−\mathrm{2}\theta\right)\:\mathrm{tan}\:\theta}{\mathrm{2sin}\:\phi\:+\mathrm{sin}\:\left(\phi+\mathrm{2}\theta\right)} \\ $$
Commented by ajfour last updated on 04/Feb/18
![thanks Sir! I could obtain, taking D as origin A=((a^2 tan^2 𝛉)/(2[tan 𝛉+(((2tan 𝛗 tan 2𝛉)/(tan 2𝛉−tan 𝛗)))])) had not rearranged.](https://www.tinkutara.com/question/Q29115.png)
$${thanks}\:{Sir}! \\ $$$${I}\:{could}\:{obtain},\:{taking}\:{D}\:{as}\:{origin} \\ $$$${A}=\frac{\boldsymbol{{a}}^{\mathrm{2}} \mathrm{tan}\:^{\mathrm{2}} \boldsymbol{\theta}}{\mathrm{2}\left[\mathrm{tan}\:\boldsymbol{\theta}+\left(\frac{\mathrm{2tan}\:\boldsymbol{\phi}\:\mathrm{tan}\:\mathrm{2}\boldsymbol{\theta}}{\mathrm{tan}\:\mathrm{2}\boldsymbol{\theta}−\mathrm{tan}\:\boldsymbol{\phi}}\right)\right]} \\ $$$${had}\:{not}\:{rearranged}. \\ $$
