Menu Close

Question-29134

Tinku Tara 0 Comments
Pin




Question Number 29134 by Tinkutara last updated on 04/Feb/18
Commented by ajfour last updated on 04/Feb/18
Commented by ajfour last updated on 04/Feb/18
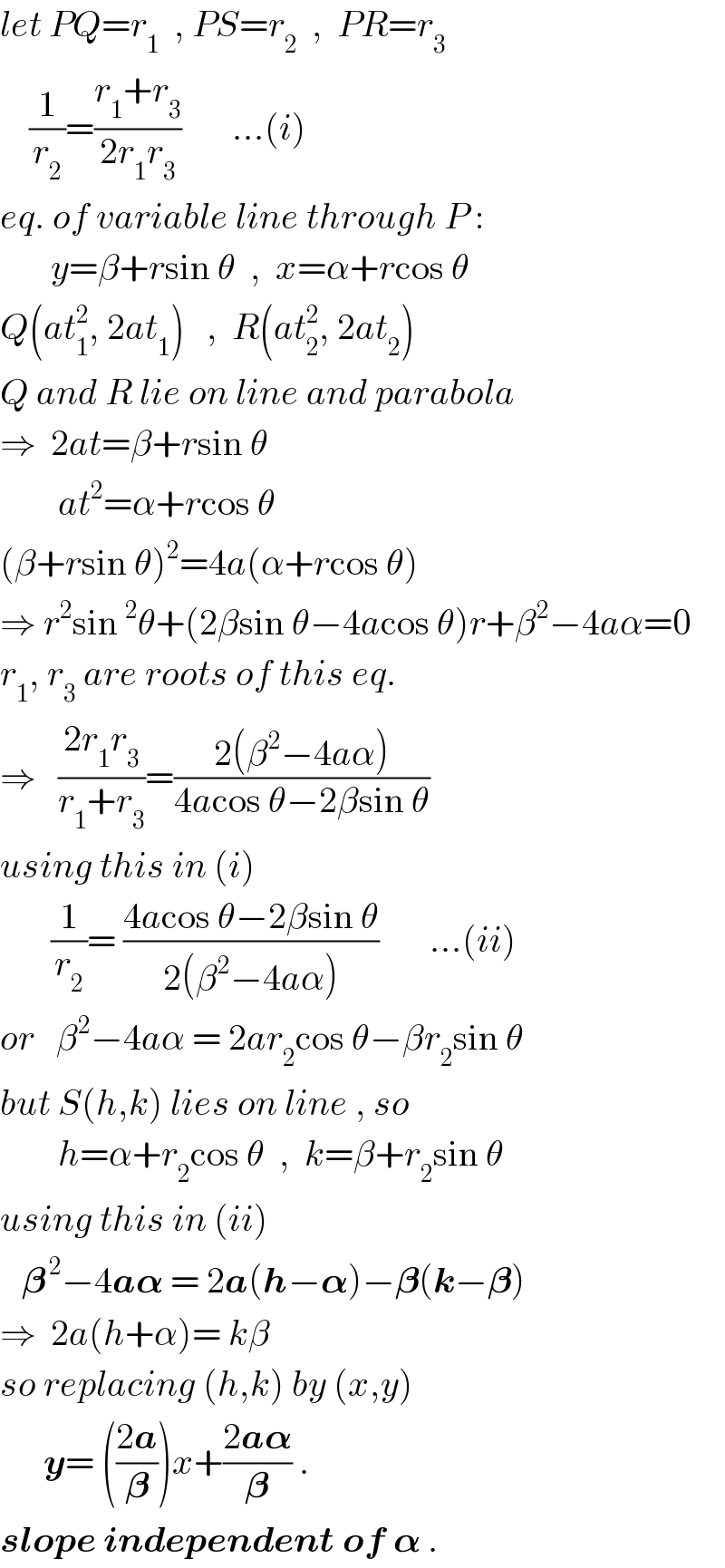
let PQ=r_1 , PS=r_2 , PR=r_3 (1/r_2 )=((r_1 +r_3 )/(2r_1 r_3 )) ...(i) eq. of variable line through P : y=β+rsin θ , x=α+rcos θ Q(at_1 ^2 , 2at_1 ) , R(at_2 ^2 , 2at_2 ) Q and R lie on line and parabola ⇒ 2at=β+rsin θ at^2 =α+rcos θ (β+rsin θ)^2 =4a(α+rcos θ) ⇒ r^2 sin^2 θ+(2βsin θ−4acos θ)r+β^2 −4aα=0 r_1 , r_3 are roots of this eq. ⇒ ((2r_1 r_3 )/(r_1 +r_3 ))=((2(β^2 −4aα))/(4acos θ−2βsin θ)) using this in (i) (1/r_2 )= ((4acos θ−2βsin θ)/(2(β^2 −4aα))) ...(ii) or β^2 −4aα = 2ar_2 cos θ−βr_2 sin θ but S(h,k) lies on line , so h=α+r_2 cos θ , k=β+r_2 sin θ using this in (ii) 𝛃^( 2) −4a𝛂 = 2a(h−𝛂)−𝛃(k−𝛃) ⇒ 2a(h+α)= kβ so replacing (h,k) by (x,y) y= (((2a)/𝛃))x+((2a𝛂)/𝛃) . slope independent of 𝛂 .
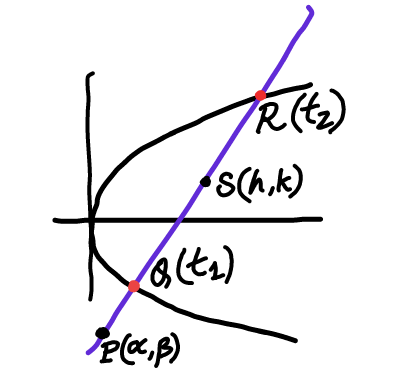
$${let}\:{PQ}={r}_{\mathrm{1}} \:\:,\:{PS}={r}_{\mathrm{2}} \:\:,\:\:{PR}={r}_{\mathrm{3}} \\ $$$$\:\:\:\:\frac{\mathrm{1}}{{r}_{\mathrm{2}} }=\frac{{r}_{\mathrm{1}} +{r}_{\mathrm{3}} }{\mathrm{2}{r}_{\mathrm{1}} {r}_{\mathrm{3}} }\:\:\:\:\:\:\:…\left({i}\right) \\ $$$${eq}.\:{of}\:{variable}\:{line}\:{through}\:{P}\:: \\ $$$$\:\:\:\:\:\:\:{y}=\beta+{r}\mathrm{sin}\:\theta\:\:,\:\:{x}=\alpha+{r}\mathrm{cos}\:\theta \\ $$$${Q}\left({at}_{\mathrm{1}} ^{\mathrm{2}} ,\:\mathrm{2}{at}_{\mathrm{1}} \right)\:\:\:,\:\:{R}\left({at}_{\mathrm{2}} ^{\mathrm{2}} ,\:\mathrm{2}{at}_{\mathrm{2}} \right) \\ $$$${Q}\:{and}\:{R}\:{lie}\:{on}\:{line}\:{and}\:{parabola} \\ $$$$\Rightarrow\:\:\mathrm{2}{at}=\beta+{r}\mathrm{sin}\:\theta \\ $$$$\:\:\:\:\:\:\:\:{at}^{\mathrm{2}} =\alpha+{r}\mathrm{cos}\:\theta \\ $$$$\left(\beta+{r}\mathrm{sin}\:\theta\right)^{\mathrm{2}} =\mathrm{4}{a}\left(\alpha+{r}\mathrm{cos}\:\theta\right) \\ $$$$\Rightarrow\:{r}^{\mathrm{2}} \mathrm{sin}\:^{\mathrm{2}} \theta+\left(\mathrm{2}\beta\mathrm{sin}\:\theta−\mathrm{4}{a}\mathrm{cos}\:\theta\right){r}+\beta^{\mathrm{2}} −\mathrm{4}{a}\alpha=\mathrm{0} \\ $$$${r}_{\mathrm{1}} ,\:{r}_{\mathrm{3}} \:{are}\:{roots}\:{of}\:{this}\:{eq}. \\ $$$$\Rightarrow\:\:\:\frac{\mathrm{2}{r}_{\mathrm{1}} {r}_{\mathrm{3}} }{{r}_{\mathrm{1}} +{r}_{\mathrm{3}} }=\frac{\mathrm{2}\left(\beta^{\mathrm{2}} −\mathrm{4}{a}\alpha\right)}{\mathrm{4}{a}\mathrm{cos}\:\theta−\mathrm{2}\beta\mathrm{sin}\:\theta} \\ $$$${using}\:{this}\:{in}\:\left({i}\right) \\ $$$$\:\:\:\:\:\:\:\frac{\mathrm{1}}{{r}_{\mathrm{2}} }=\:\frac{\mathrm{4}{a}\mathrm{cos}\:\theta−\mathrm{2}\beta\mathrm{sin}\:\theta}{\mathrm{2}\left(\beta^{\mathrm{2}} −\mathrm{4}{a}\alpha\right)}\:\:\:\:\:\:\:…\left({ii}\right) \\ $$$${or}\:\:\:\beta^{\mathrm{2}} −\mathrm{4}{a}\alpha\:=\:\mathrm{2}{ar}_{\mathrm{2}} \mathrm{cos}\:\theta−\beta{r}_{\mathrm{2}} \mathrm{sin}\:\theta \\ $$$${but}\:{S}\left({h},{k}\right)\:{lies}\:{on}\:{line}\:,\:{so} \\ $$$$\:\:\:\:\:\:\:\:{h}=\alpha+{r}_{\mathrm{2}} \mathrm{cos}\:\theta\:\:,\:\:{k}=\beta+{r}_{\mathrm{2}} \mathrm{sin}\:\theta \\ $$$${using}\:{this}\:{in}\:\left({ii}\right) \\ $$$$\:\:\:\boldsymbol{\beta}^{\:\mathrm{2}} −\mathrm{4}\boldsymbol{{a}\alpha}\:=\:\mathrm{2}\boldsymbol{{a}}\left(\boldsymbol{{h}}−\boldsymbol{\alpha}\right)−\boldsymbol{\beta}\left(\boldsymbol{{k}}−\boldsymbol{\beta}\right) \\ $$$$\Rightarrow\:\:\mathrm{2}{a}\left({h}+\alpha\right)=\:{k}\beta \\ $$$${so}\:{replacing}\:\left({h},{k}\right)\:{by}\:\left({x},{y}\right) \\ $$$$\:\:\:\:\:\:\boldsymbol{{y}}=\:\left(\frac{\mathrm{2}\boldsymbol{{a}}}{\boldsymbol{\beta}}\right){x}+\frac{\mathrm{2}\boldsymbol{{a}\alpha}}{\boldsymbol{\beta}}\:. \\ $$$$\boldsymbol{{slope}}\:\boldsymbol{{independent}}\:\boldsymbol{{of}}\:\boldsymbol{\alpha}\:. \\ $$
Commented by Tinkutara last updated on 05/Feb/18
Wonderful Sir! ���� Thanks! ��

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *