Question Number 29362 by puneet1789 last updated on 08/Feb/18
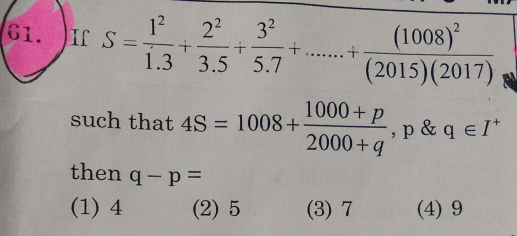
Commented by puneet1789 last updated on 08/Feb/18
how..?
Commented by math solver last updated on 08/Feb/18

$${option}\left(\mathrm{4}\right)=\mathrm{9}?? \\ $$
Answered by math solver last updated on 08/Feb/18
![T_n = (n^2 /((2n−1)(2n+1))) ⇒ (((2n−1)(2n+1)+1)/(4(2n−1)(2n+1))) ⇒ (1/4)[ 1+(1/((2n−1)(2n+1)))] ⇒(1/4)[ 1+ (1/2)((1/(2n−1))−(1/(2n+1)))] Therefore, S_n = (1/4)[ Σ1+ (1/2)Σ((1/(2n−1))−(1/(2n+1)))] ⇒ (1/4)[ n + (1/2)(1−(1/(2n+1)))] ⇒(1/4)( n+(n/(2n+1))) ⇒((n(2n+2))/(4(2n+1))) ⇒((n(n+1))/(2(2n+1))). So,S = ((1008(1009))/(2(2017))) and 4S= 1008 + ((1000+8)/(2000+17)). then , q −p= 9.](https://www.tinkutara.com/question/Q29393.png)
$${T}_{{n}} \:=\:\frac{{n}^{\mathrm{2}} }{\left(\mathrm{2}{n}−\mathrm{1}\right)\left(\mathrm{2}{n}+\mathrm{1}\right)} \\ $$$$\Rightarrow\:\frac{\left(\mathrm{2}{n}−\mathrm{1}\right)\left(\mathrm{2}{n}+\mathrm{1}\right)+\mathrm{1}}{\mathrm{4}\left(\mathrm{2}{n}−\mathrm{1}\right)\left(\mathrm{2}{n}+\mathrm{1}\right)} \\ $$$$\Rightarrow\:\frac{\mathrm{1}}{\mathrm{4}}\left[\:\mathrm{1}+\frac{\mathrm{1}}{\left(\mathrm{2}{n}−\mathrm{1}\right)\left(\mathrm{2}{n}+\mathrm{1}\right)}\right] \\ $$$$\Rightarrow\frac{\mathrm{1}}{\mathrm{4}}\left[\:\mathrm{1}+\:\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{\mathrm{1}}{\mathrm{2}{n}−\mathrm{1}}−\frac{\mathrm{1}}{\mathrm{2}{n}+\mathrm{1}}\right)\right] \\ $$$${Therefore}, \\ $$$${S}_{{n}} \:=\:\frac{\mathrm{1}}{\mathrm{4}}\left[\:\Sigma\mathrm{1}+\:\frac{\mathrm{1}}{\mathrm{2}}\Sigma\left(\frac{\mathrm{1}}{\mathrm{2}{n}−\mathrm{1}}−\frac{\mathrm{1}}{\mathrm{2}{n}+\mathrm{1}}\right)\right] \\ $$$$\Rightarrow\:\frac{\mathrm{1}}{\mathrm{4}}\left[\:{n}\:+\:\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}{n}+\mathrm{1}}\right)\right] \\ $$$$\Rightarrow\frac{\mathrm{1}}{\mathrm{4}}\left(\:{n}+\frac{{n}}{\mathrm{2}{n}+\mathrm{1}}\right) \\ $$$$\Rightarrow\frac{{n}\left(\mathrm{2}{n}+\mathrm{2}\right)}{\mathrm{4}\left(\mathrm{2}{n}+\mathrm{1}\right)} \\ $$$$\Rightarrow\frac{{n}\left({n}+\mathrm{1}\right)}{\mathrm{2}\left(\mathrm{2}{n}+\mathrm{1}\right)}. \\ $$$${So},{S}\:=\:\frac{\mathrm{1008}\left(\mathrm{1009}\right)}{\mathrm{2}\left(\mathrm{2017}\right)} \\ $$$${and}\:\mathrm{4}{S}=\:\mathrm{1008}\:+\:\frac{\mathrm{1000}+\mathrm{8}}{\mathrm{2000}+\mathrm{17}}. \\ $$$${then}\:,\:{q}\:−{p}=\:\mathrm{9}. \\ $$
Commented by Rasheed.Sindhi last updated on 08/Feb/18
₪î¢3 ДÞÞЯøД¢ђ!
Commented by NECx last updated on 08/Feb/18
$${really}\:{nice}\:{approach} \\ $$
Commented by math solver last updated on 08/Feb/18

$$\left.{thank}\:{you}\:!:\right) \\ $$
Commented by puneet1789 last updated on 08/Feb/18
vry nice sir.. thnku
