Question Number 29424 by Tinkutara last updated on 08/Feb/18
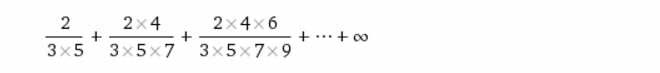
Commented by prof Abdo imad last updated on 09/Feb/18
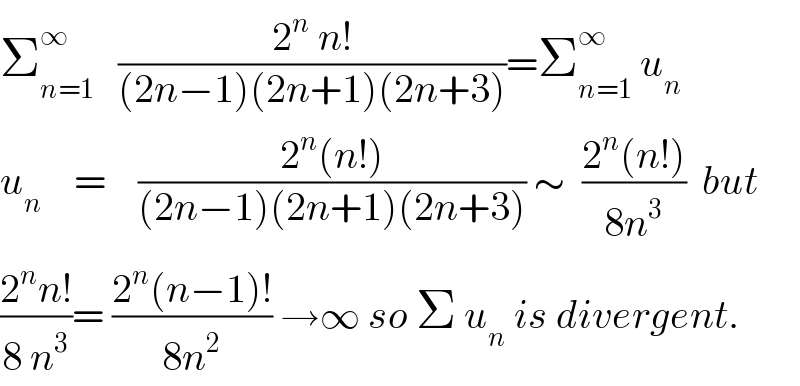
$$\sum_{{n}=\mathrm{1}} ^{\infty} \:\:\:\frac{\mathrm{2}^{{n}} \:{n}!}{\left(\mathrm{2}{n}−\mathrm{1}\right)\left(\mathrm{2}{n}+\mathrm{1}\right)\left(\mathrm{2}{n}+\mathrm{3}\right)}=\sum_{{n}=\mathrm{1}} ^{\infty} \:{u}_{{n}} \\ $$$${u}_{{n}} \:\:\:\:=\:\:\:\:\frac{\mathrm{2}^{{n}} \left({n}!\right)}{\left(\mathrm{2}{n}−\mathrm{1}\right)\left(\mathrm{2}{n}+\mathrm{1}\right)\left(\mathrm{2}{n}+\mathrm{3}\right)}\:\sim\:\:\frac{\mathrm{2}^{{n}} \left({n}!\right)}{\mathrm{8}{n}^{\mathrm{3}} }\:\:{but} \\ $$$$\frac{\mathrm{2}^{{n}} {n}!}{\mathrm{8}\:{n}^{\mathrm{3}} }=\:\frac{\mathrm{2}^{{n}} \left({n}−\mathrm{1}\right)!}{\mathrm{8}{n}^{\mathrm{2}} }\:\rightarrow\infty\:{so}\:\Sigma\:{u}_{{n}} \:{is}\:{divergent}. \\ $$
Commented by math solver last updated on 09/Feb/18
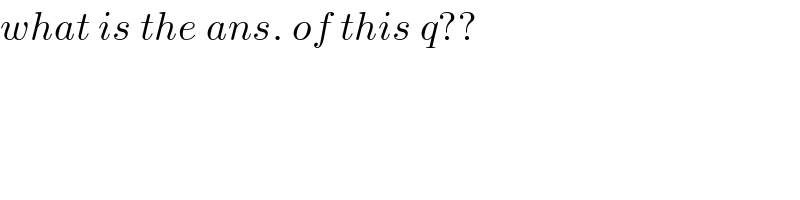
$${what}\:{is}\:{the}\:{ans}.\:{of}\:{this}\:{q}?? \\ $$
Commented by Tinkutara last updated on 12/Feb/18
Sorry it was not my solution. I saw on internet that the answer is 2/3. Solution is also there.
Commented by ajfour last updated on 12/Feb/18
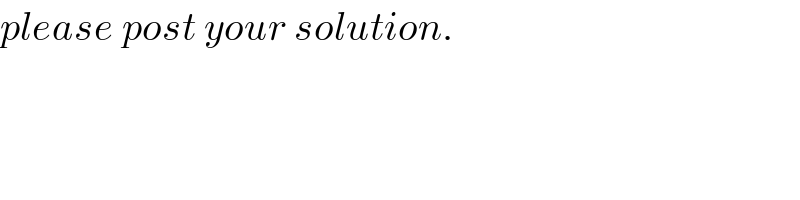
$${please}\:{post}\:{your}\:{solution}. \\ $$
Commented by prof Abdo imad last updated on 12/Feb/18
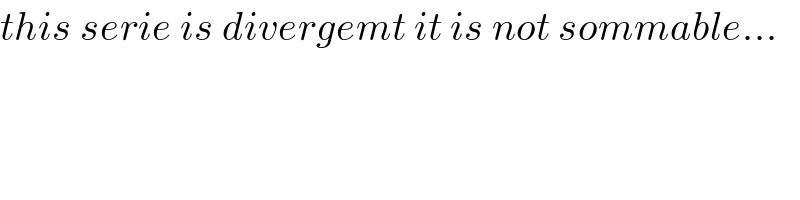
$${this}\:{serie}\:{is}\:{divergemt}\:{it}\:{is}\:{not}\:{sommable}… \\ $$
Commented by rahul 19 last updated on 12/Feb/18

$${ummm},\:{isn}'{t}\:{it}\:{insane}? \\ $$$${one}\:{time}\:{prof}\:{abdo}\:{clearly}\:{proof}\:\: \\ $$$${series}\:{diverges}\:{but}\:{ans}.\:{is}\:\mathrm{2}/\mathrm{3}.\: \\ $$$${how}'{s}\:{that}\:{possible}\:? \\ $$
Commented by rahul 19 last updated on 12/Feb/18

$${ohh},{yes}!\: \\ $$
Commented by Tinkutara last updated on 12/Feb/18
https://artofproblemsolving.com/community/q1h1588848p9844077
