Question Number 29425 by puneet1789 last updated on 08/Feb/18

Commented by prof Abdo imad last updated on 12/Feb/18
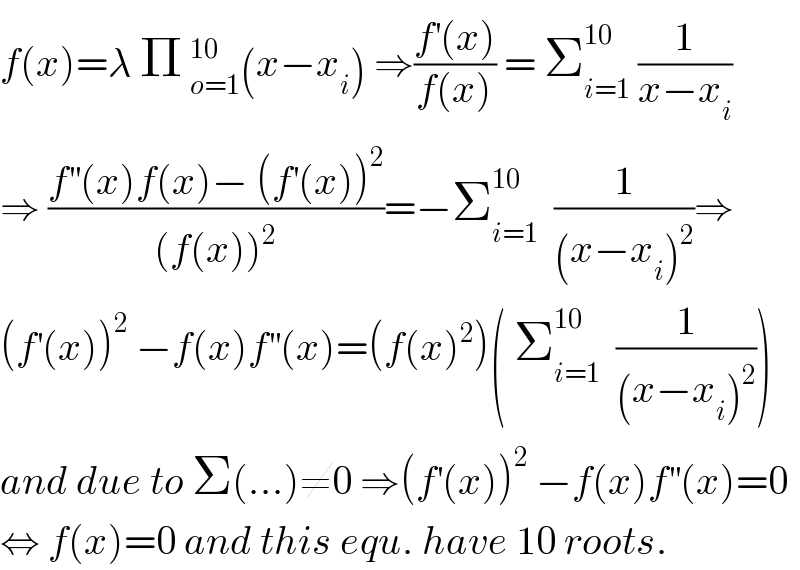
$${f}\left({x}\right)=\lambda\:\Pi\:_{{o}=\mathrm{1}} ^{\mathrm{10}} \left({x}−{x}_{{i}} \right)\:\Rightarrow\frac{{f}^{'} \left({x}\right)}{{f}\left({x}\right)}\:=\:\sum_{{i}=\mathrm{1}} ^{\mathrm{10}} \:\frac{\mathrm{1}}{{x}−{x}_{{i}} } \\ $$$$\Rightarrow\:\frac{{f}^{''} \left({x}\right){f}\left({x}\right)−\:\left({f}^{'} \left({x}\right)\right)^{\mathrm{2}} }{\left({f}\left({x}\right)\right)^{\mathrm{2}} }=−\sum_{{i}=\mathrm{1}} ^{\mathrm{10}} \:\:\frac{\mathrm{1}}{\left({x}−{x}_{{i}} \right)^{\mathrm{2}} }\Rightarrow \\ $$$$\left({f}^{'} \left({x}\right)\right)^{\mathrm{2}} \:−{f}\left({x}\right){f}^{''} \left({x}\right)=\left({f}\left({x}\right)^{\mathrm{2}} \right)\left(\:\sum_{{i}=\mathrm{1}} ^{\mathrm{10}} \:\:\frac{\mathrm{1}}{\left({x}−{x}_{{i}} \right)^{\mathrm{2}} }\right) \\ $$$${and}\:{due}\:{to}\:\Sigma\left(…\right)\neq\mathrm{0}\:\Rightarrow\left({f}^{'} \left({x}\right)\right)^{\mathrm{2}} \:−{f}\left({x}\right){f}^{''} \left({x}\right)=\mathrm{0} \\ $$$$\Leftrightarrow\:{f}\left({x}\right)=\mathrm{0}\:{and}\:{this}\:{equ}.\:{have}\:\mathrm{10}\:{roots}. \\ $$
Answered by mrW2 last updated on 09/Feb/18
![f(x)=(x−a_1 )(x−a_2 )...(x−a_(10) ) f′(x)=f(x)((1/(x−a_1 ))+(1/(x−a_2 ))+...+(1/(x−a_(10) ))) f′′(x)=f(x)((1/(x−a_1 ))+(1/(x−a_2 ))+...+(1/(x−a_(10) )))^2 −f(x)[(1/((x−a_1 )^2 ))+(1/((x−a_2 )^2 ))+...+(1/((x−a_(10) )^2 ))] ⇒f(x)f′′(x)=f^2 (x)((1/(x−a_1 ))+(1/(x−a_2 ))+...+(1/(x−a_(10) )))^2 −f^2 (x)[(1/((x−a_1 )^2 ))+(1/((x−a_2 )^2 ))+...+(1/((x−a_(10) )^2 ))] ⇒f(x)f′′(x)=[f′(x)]^2 −f^2 (x)[(1/((x−a_1 )^2 ))+(1/((x−a_2 )^2 ))+...+(1/((x−a_(10) )^2 ))] ⇒f(x)f′′(x)−[f′(x)]^2 =−f^2 (x)[(1/((x−a_1 )^2 ))+(1/((x−a_2 )^2 ))+...+(1/((x−a_(10) )^2 ))]=0 i.e. f(x)f′′(x)−[f′(x)]^2 =0 has the same roots as f(x)=0, i.e. 10 real roots. ⇒answer (2) is right.](https://www.tinkutara.com/question/Q29432.png)
$${f}\left({x}\right)=\left({x}−{a}_{\mathrm{1}} \right)\left({x}−{a}_{\mathrm{2}} \right)…\left({x}−{a}_{\mathrm{10}} \right) \\ $$$${f}'\left({x}\right)={f}\left({x}\right)\left(\frac{\mathrm{1}}{{x}−{a}_{\mathrm{1}} }+\frac{\mathrm{1}}{{x}−{a}_{\mathrm{2}} }+…+\frac{\mathrm{1}}{{x}−{a}_{\mathrm{10}} }\right) \\ $$$${f}''\left({x}\right)={f}\left({x}\right)\left(\frac{\mathrm{1}}{{x}−{a}_{\mathrm{1}} }+\frac{\mathrm{1}}{{x}−{a}_{\mathrm{2}} }+…+\frac{\mathrm{1}}{{x}−{a}_{\mathrm{10}} }\right)^{\mathrm{2}} −{f}\left({x}\right)\left[\frac{\mathrm{1}}{\left({x}−{a}_{\mathrm{1}} \right)^{\mathrm{2}} }+\frac{\mathrm{1}}{\left({x}−{a}_{\mathrm{2}} \right)^{\mathrm{2}} }+…+\frac{\mathrm{1}}{\left({x}−{a}_{\mathrm{10}} \right)^{\mathrm{2}} }\right] \\ $$$$\Rightarrow{f}\left({x}\right){f}''\left({x}\right)={f}^{\mathrm{2}} \left({x}\right)\left(\frac{\mathrm{1}}{{x}−{a}_{\mathrm{1}} }+\frac{\mathrm{1}}{{x}−{a}_{\mathrm{2}} }+…+\frac{\mathrm{1}}{{x}−{a}_{\mathrm{10}} }\right)^{\mathrm{2}} −{f}^{\mathrm{2}} \left({x}\right)\left[\frac{\mathrm{1}}{\left({x}−{a}_{\mathrm{1}} \right)^{\mathrm{2}} }+\frac{\mathrm{1}}{\left({x}−{a}_{\mathrm{2}} \right)^{\mathrm{2}} }+…+\frac{\mathrm{1}}{\left({x}−{a}_{\mathrm{10}} \right)^{\mathrm{2}} }\right] \\ $$$$\Rightarrow{f}\left({x}\right){f}''\left({x}\right)=\left[{f}'\left({x}\right)\right]^{\mathrm{2}} −{f}^{\mathrm{2}} \left({x}\right)\left[\frac{\mathrm{1}}{\left({x}−{a}_{\mathrm{1}} \right)^{\mathrm{2}} }+\frac{\mathrm{1}}{\left({x}−{a}_{\mathrm{2}} \right)^{\mathrm{2}} }+…+\frac{\mathrm{1}}{\left({x}−{a}_{\mathrm{10}} \right)^{\mathrm{2}} }\right] \\ $$$$\Rightarrow{f}\left({x}\right){f}''\left({x}\right)−\left[{f}'\left({x}\right)\right]^{\mathrm{2}} =−{f}^{\mathrm{2}} \left({x}\right)\left[\frac{\mathrm{1}}{\left({x}−{a}_{\mathrm{1}} \right)^{\mathrm{2}} }+\frac{\mathrm{1}}{\left({x}−{a}_{\mathrm{2}} \right)^{\mathrm{2}} }+…+\frac{\mathrm{1}}{\left({x}−{a}_{\mathrm{10}} \right)^{\mathrm{2}} }\right]=\mathrm{0} \\ $$$${i}.{e}.\:{f}\left({x}\right){f}''\left({x}\right)−\left[{f}'\left({x}\right)\right]^{\mathrm{2}} =\mathrm{0}\:{has}\:{the}\:{same} \\ $$$${roots}\:{as}\:{f}\left({x}\right)=\mathrm{0},\:{i}.{e}.\:\mathrm{10}\:{real}\:{roots}. \\ $$$$\Rightarrow{answer}\:\left(\mathrm{2}\right)\:{is}\:{right}. \\ $$
Commented by puneet1789 last updated on 08/Feb/18
vry nice sir.. thank you
