Menu Close

Question-29522

Tinku Tara 0 Comments
Pin




Question Number 29522 by 803jaideep@gmail.com last updated on 09/Feb/18
Commented by 803jaideep@gmail.com last updated on 09/Feb/18
40th ques sry
$$\mathrm{40th}\:\mathrm{ques}\:\mathrm{sry} \\ $$
Commented by Tinkutara last updated on 09/Feb/18
120?
Commented by 803jaideep@gmail.com last updated on 09/Feb/18
yes yes but how
$$\mathrm{yes}\:\mathrm{yes}\:\mathrm{but}\:\mathrm{how} \\ $$
Commented by Tinkutara last updated on 09/Feb/18
See Q 20739
Commented by math solver last updated on 10/Feb/18
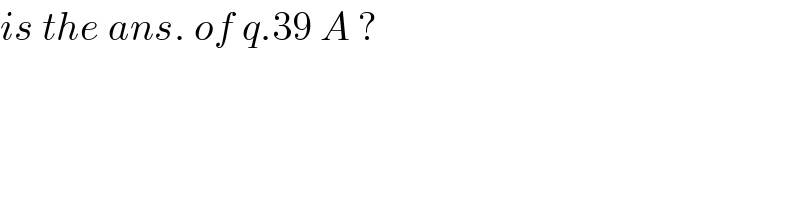
is the ans. of q.39 A ?
$${is}\:{the}\:{ans}.\:{of}\:{q}.\mathrm{39}\:{A}\:? \\ $$
Commented by prof Abdo imad last updated on 11/Feb/18
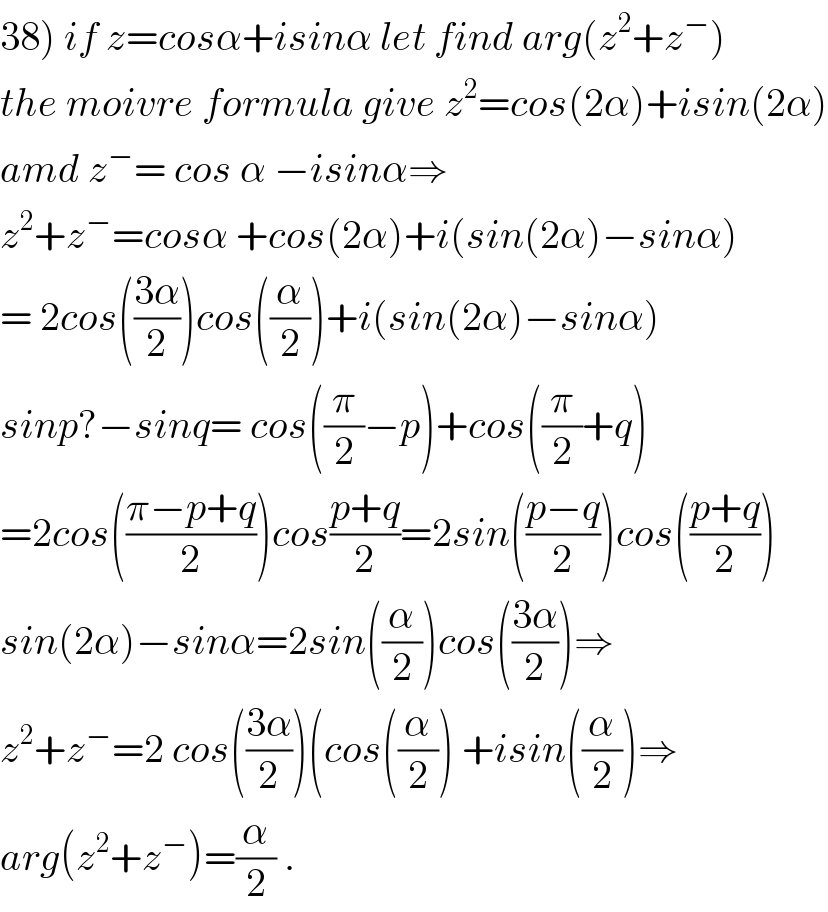
38) if z=cosα+isinα let find arg(z^2 +z^− ) the moivre formula give z^2 =cos(2α)+isin(2α) amd z^− = cos α −isinα⇒ z^2 +z^− =cosα +cos(2α)+i(sin(2α)−sinα) = 2cos(((3α)/2))cos((α/2))+i(sin(2α)−sinα) sinp?−sinq= cos((π/2)−p)+cos((π/2)+q) =2cos(((π−p+q)/2))cos((p+q)/2)=2sin(((p−q)/2))cos(((p+q)/2)) sin(2α)−sinα=2sin((α/2))cos(((3α)/2))⇒ z^2 +z^− =2 cos(((3α)/2))(cos((α/2)) +isin((α/2))⇒ arg(z^2 +z^− )=(α/2) .
$$\left.\mathrm{38}\right)\:{if}\:{z}={cos}\alpha+{isin}\alpha\:{let}\:{find}\:{arg}\left({z}^{\mathrm{2}} +{z}^{−} \right) \\ $$$${the}\:{moivre}\:{formula}\:{give}\:{z}^{\mathrm{2}} ={cos}\left(\mathrm{2}\alpha\right)+{isin}\left(\mathrm{2}\alpha\right) \\ $$$${amd}\:{z}^{−} =\:{cos}\:\alpha\:−{isin}\alpha\Rightarrow \\ $$$${z}^{\mathrm{2}} +{z}^{−} ={cos}\alpha\:+{cos}\left(\mathrm{2}\alpha\right)+{i}\left({sin}\left(\mathrm{2}\alpha\right)−{sin}\alpha\right) \\ $$$$=\:\mathrm{2}{cos}\left(\frac{\mathrm{3}\alpha}{\mathrm{2}}\right){cos}\left(\frac{\alpha}{\mathrm{2}}\right)+{i}\left({sin}\left(\mathrm{2}\alpha\right)−{sin}\alpha\right) \\ $$$${sinp}?−{sinq}=\:{cos}\left(\frac{\pi}{\mathrm{2}}−{p}\right)+{cos}\left(\frac{\pi}{\mathrm{2}}+{q}\right) \\ $$$$=\mathrm{2}{cos}\left(\frac{\pi−{p}+{q}}{\mathrm{2}}\right){cos}\frac{{p}+{q}}{\mathrm{2}}=\mathrm{2}{sin}\left(\frac{{p}−{q}}{\mathrm{2}}\right){cos}\left(\frac{{p}+{q}}{\mathrm{2}}\right) \\ $$$${sin}\left(\mathrm{2}\alpha\right)−{sin}\alpha=\mathrm{2}{sin}\left(\frac{\alpha}{\mathrm{2}}\right){cos}\left(\frac{\mathrm{3}\alpha}{\mathrm{2}}\right)\Rightarrow \\ $$$${z}^{\mathrm{2}} +{z}^{−} =\mathrm{2}\:{cos}\left(\frac{\mathrm{3}\alpha}{\mathrm{2}}\right)\left({cos}\left(\frac{\alpha}{\mathrm{2}}\right)\:+{isin}\left(\frac{\alpha}{\mathrm{2}}\right)\Rightarrow\right. \\ $$$${arg}\left({z}^{\mathrm{2}} +{z}^{−} \right)=\frac{\alpha}{\mathrm{2}}\:. \\ $$
Commented by math solver last updated on 11/Feb/18
wow,sir.
$$\mathrm{wow},\mathrm{sir}. \\ $$
Answered by 803jaideep@gmail.com last updated on 09/Feb/18
10th
$$\mathrm{10th} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *