Question Number 29541 by naka3546 last updated on 09/Feb/18

Commented by naka3546 last updated on 09/Feb/18
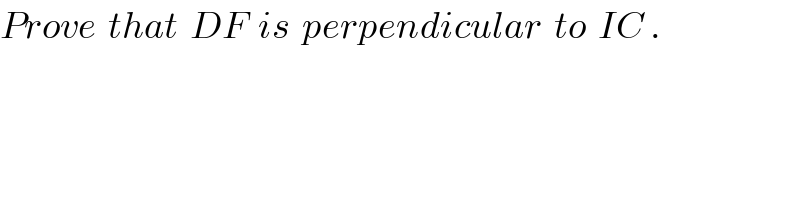
$${Prove}\:\:{that}\:\:{DF}\:\:{is}\:\:{perpendicular}\:\:{to}\:\:{IC}\:. \\ $$
Commented by ajfour last updated on 09/Feb/18

Commented by ajfour last updated on 09/Feb/18

$$\mathrm{tan}\:\theta=\frac{{c}−{a}\mathrm{cos}\:\alpha−{a}\mathrm{sin}\:\alpha}{{a}\mathrm{cos}\:\alpha−{a}\mathrm{sin}\:\alpha} \\ $$$$\mathrm{tan}\:\phi=\frac{{b}\mathrm{cos}\:\beta−{b}\mathrm{sin}\:\beta}{{c}−{b}\mathrm{cos}\:\beta−{b}\mathrm{sin}\:\beta} \\ $$$${and}\:{since}\:\:\:{a}\mathrm{cos}\:\alpha+{b}\mathrm{cos}\:\beta={c} \\ $$$${also}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{a}\mathrm{sin}\:\alpha={b}\mathrm{sin}\:\beta \\ $$$${therefore}\:\:\:\:\mathrm{tan}\:\boldsymbol{\theta}\:=\:\mathrm{tan}\:\boldsymbol{\phi} \\ $$$$\:\:\:\:\:\:{so}\:\:\:{DF}\:\bot\:{to}\:{IC}\:\:. \\ $$
Commented by mrW2 last updated on 09/Feb/18
Great!
