Menu Close

Question-29550

Tinku Tara 0 Comments
Pin




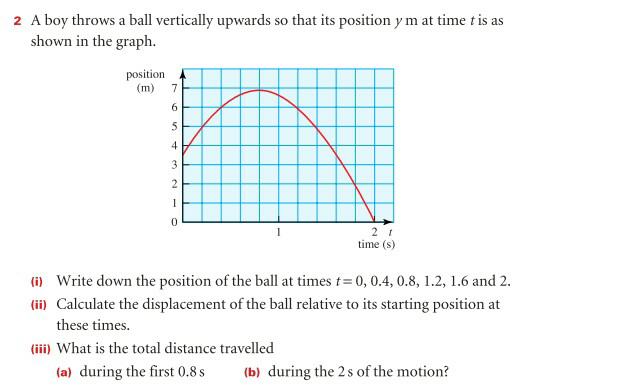
Question Number 29550 by tawa tawa last updated on 09/Feb/18
Answered by ajfour last updated on 10/Feb/18
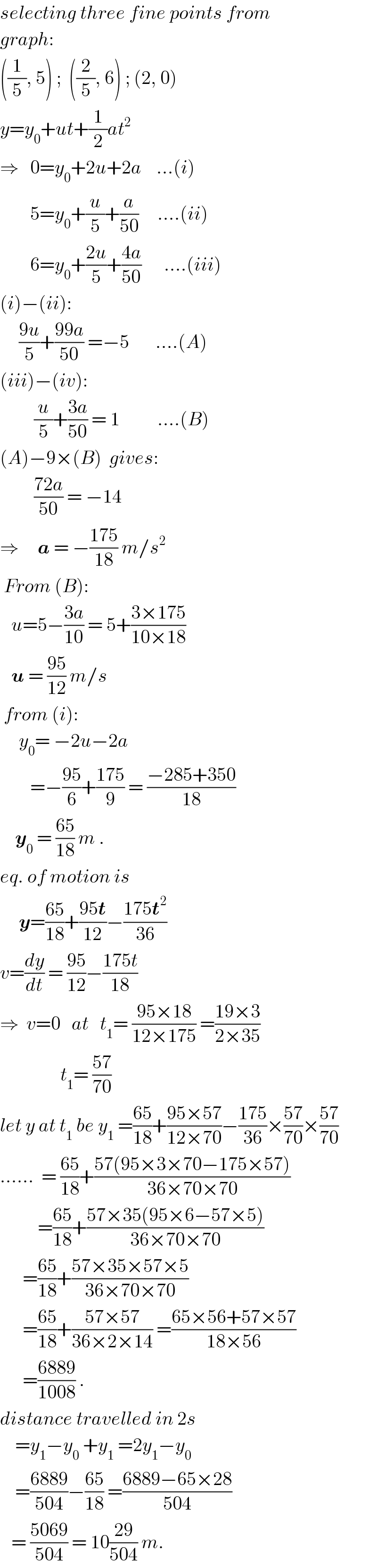
selecting three fine points from graph: ((1/5), 5) ; ((2/5), 6) ; (2, 0) y=y_0 +ut+(1/2)at^2 ⇒ 0=y_0 +2u+2a ...(i) 5=y_0 +(u/5)+(a/(50)) ....(ii) 6=y_0 +((2u)/5)+((4a)/(50)) ....(iii) (i)−(ii): ((9u)/5)+((99a)/(50)) =−5 ....(A) (iii)−(iv): (u/5)+((3a)/(50)) = 1 ....(B) (A)−9×(B) gives: ((72a)/(50)) = −14 ⇒ a = −((175)/(18)) m/s^2 From (B): u=5−((3a)/(10)) = 5+((3×175)/(10×18)) u = ((95)/(12)) m/s from (i): y_0 = −2u−2a =−((95)/6)+((175)/9) = ((−285+350)/(18)) y_0 = ((65)/(18)) m . eq. of motion is y=((65)/(18))+((95t)/(12))−((175t^2 )/(36)) v=(dy/dt) = ((95)/(12))−((175t)/(18)) ⇒ v=0 at t_1 = ((95×18)/(12×175)) =((19×3)/(2×35)) t_1 = ((57)/(70)) let y at t_1 be y_1 =((65)/(18))+((95×57)/(12×70))−((175)/(36))×((57)/(70))×((57)/(70)) ...... = ((65)/(18))+((57(95×3×70−175×57))/(36×70×70)) =((65)/(18))+((57×35(95×6−57×5))/(36×70×70)) =((65)/(18))+((57×35×57×5)/(36×70×70)) =((65)/(18))+((57×57)/(36×2×14)) =((65×56+57×57)/(18×56)) =((6889)/(1008)) . distance travelled in 2s =y_1 −y_0 +y_1 =2y_1 −y_0 =((6889)/(504))−((65)/(18)) =((6889−65×28)/(504)) = ((5069)/(504)) = 10((29)/(504)) m.
$${selecting}\:{three}\:{fine}\:{points}\:{from} \\ $$$${graph}: \\ $$$$\left(\frac{\mathrm{1}}{\mathrm{5}},\:\mathrm{5}\right)\:;\:\:\left(\frac{\mathrm{2}}{\mathrm{5}},\:\mathrm{6}\right)\:;\:\left(\mathrm{2},\:\mathrm{0}\right) \\ $$$${y}={y}_{\mathrm{0}} +{ut}+\frac{\mathrm{1}}{\mathrm{2}}{at}^{\mathrm{2}} \\ $$$$\Rightarrow\:\:\:\mathrm{0}={y}_{\mathrm{0}} +\mathrm{2}{u}+\mathrm{2}{a}\:\:\:\:…\left({i}\right) \\ $$$$\:\:\:\:\:\:\:\:\mathrm{5}={y}_{\mathrm{0}} +\frac{{u}}{\mathrm{5}}+\frac{{a}}{\mathrm{50}}\:\:\:\:\:….\left({ii}\right) \\ $$$$\:\:\:\:\:\:\:\:\mathrm{6}={y}_{\mathrm{0}} +\frac{\mathrm{2}{u}}{\mathrm{5}}+\frac{\mathrm{4}{a}}{\mathrm{50}}\:\:\:\:\:\:….\left({iii}\right) \\ $$$$\left({i}\right)−\left({ii}\right): \\ $$$$\:\:\:\:\:\frac{\mathrm{9}{u}}{\mathrm{5}}+\frac{\mathrm{99}{a}}{\mathrm{50}}\:=−\mathrm{5}\:\:\:\:\:\:\:….\left({A}\right) \\ $$$$\left({iii}\right)−\left({iv}\right): \\ $$$$\:\:\:\:\:\:\:\:\:\frac{{u}}{\mathrm{5}}+\frac{\mathrm{3}{a}}{\mathrm{50}}\:=\:\mathrm{1}\:\:\:\:\:\:\:\:\:\:….\left({B}\right) \\ $$$$\left({A}\right)−\mathrm{9}×\left({B}\right)\:\:{gives}: \\ $$$$\:\:\:\:\:\:\:\:\:\frac{\mathrm{72}{a}}{\mathrm{50}}\:=\:−\mathrm{14} \\ $$$$\Rightarrow\:\:\:\:\:\boldsymbol{{a}}\:=\:−\frac{\mathrm{175}}{\mathrm{18}}\:{m}/{s}^{\mathrm{2}} \\ $$$$\:{From}\:\left({B}\right):\:\: \\ $$$$\:\:\:{u}=\mathrm{5}−\frac{\mathrm{3}{a}}{\mathrm{10}}\:=\:\mathrm{5}+\frac{\mathrm{3}×\mathrm{175}}{\mathrm{10}×\mathrm{18}}\: \\ $$$$\:\:\:\boldsymbol{{u}}\:=\:\frac{\mathrm{95}}{\mathrm{12}}\:{m}/{s} \\ $$$$\:{from}\:\left({i}\right): \\ $$$$\:\:\:\:\:{y}_{\mathrm{0}} =\:−\mathrm{2}{u}−\mathrm{2}{a} \\ $$$$\:\:\:\:\:\:\:\:=−\frac{\mathrm{95}}{\mathrm{6}}+\frac{\mathrm{175}}{\mathrm{9}}\:=\:\frac{−\mathrm{285}+\mathrm{350}}{\mathrm{18}} \\ $$$$\:\:\:\:\boldsymbol{{y}}_{\mathrm{0}} \:=\:\frac{\mathrm{65}}{\mathrm{18}}\:{m}\:. \\ $$$${eq}.\:{of}\:{motion}\:{is} \\ $$$$\:\:\:\:\:\boldsymbol{{y}}=\frac{\mathrm{65}}{\mathrm{18}}+\frac{\mathrm{95}\boldsymbol{{t}}}{\mathrm{12}}−\frac{\mathrm{175}\boldsymbol{{t}}^{\mathrm{2}} }{\mathrm{36}} \\ $$$${v}=\frac{{dy}}{{dt}}\:=\:\frac{\mathrm{95}}{\mathrm{12}}−\frac{\mathrm{175}{t}}{\mathrm{18}} \\ $$$$\Rightarrow\:\:{v}=\mathrm{0}\:\:\:{at}\:\:\:{t}_{\mathrm{1}} =\:\frac{\mathrm{95}×\mathrm{18}}{\mathrm{12}×\mathrm{175}}\:=\frac{\mathrm{19}×\mathrm{3}}{\mathrm{2}×\mathrm{35}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{t}_{\mathrm{1}} =\:\frac{\mathrm{57}}{\mathrm{70}}\: \\ $$$${let}\:{y}\:{at}\:{t}_{\mathrm{1}} \:{be}\:{y}_{\mathrm{1}} \:=\frac{\mathrm{65}}{\mathrm{18}}+\frac{\mathrm{95}×\mathrm{57}}{\mathrm{12}×\mathrm{70}}−\frac{\mathrm{175}}{\mathrm{36}}×\frac{\mathrm{57}}{\mathrm{70}}×\frac{\mathrm{57}}{\mathrm{70}} \\ $$$$……\:\:=\:\frac{\mathrm{65}}{\mathrm{18}}+\frac{\mathrm{57}\left(\mathrm{95}×\mathrm{3}×\mathrm{70}−\mathrm{175}×\mathrm{57}\right)}{\mathrm{36}×\mathrm{70}×\mathrm{70}} \\ $$$$\:\:\:\:\:\:\:\:\:\:=\frac{\mathrm{65}}{\mathrm{18}}+\frac{\mathrm{57}×\mathrm{35}\left(\mathrm{95}×\mathrm{6}−\mathrm{57}×\mathrm{5}\right)}{\mathrm{36}×\mathrm{70}×\mathrm{70}} \\ $$$$\:\:\:\:\:\:=\frac{\mathrm{65}}{\mathrm{18}}+\frac{\mathrm{57}×\mathrm{35}×\mathrm{57}×\mathrm{5}}{\mathrm{36}×\mathrm{70}×\mathrm{70}} \\ $$$$\:\:\:\:\:\:=\frac{\mathrm{65}}{\mathrm{18}}+\frac{\mathrm{57}×\mathrm{57}}{\mathrm{36}×\mathrm{2}×\mathrm{14}}\:=\frac{\mathrm{65}×\mathrm{56}+\mathrm{57}×\mathrm{57}}{\mathrm{18}×\mathrm{56}} \\ $$$$\:\:\:\:\:\:=\frac{\mathrm{6889}}{\mathrm{1008}}\:. \\ $$$${distance}\:{travelled}\:{in}\:\mathrm{2}{s}\: \\ $$$$\:\:\:\:={y}_{\mathrm{1}} −{y}_{\mathrm{0}} \:+{y}_{\mathrm{1}} \:=\mathrm{2}{y}_{\mathrm{1}} −{y}_{\mathrm{0}} \\ $$$$\:\:\:\:=\frac{\mathrm{6889}}{\mathrm{504}}−\frac{\mathrm{65}}{\mathrm{18}}\:=\frac{\mathrm{6889}−\mathrm{65}×\mathrm{28}}{\mathrm{504}} \\ $$$$\:\:\:=\:\frac{\mathrm{5069}}{\mathrm{504}}\:=\:\mathrm{10}\frac{\mathrm{29}}{\mathrm{504}}\:{m}. \\ $$
Commented by tawa tawa last updated on 09/Feb/18
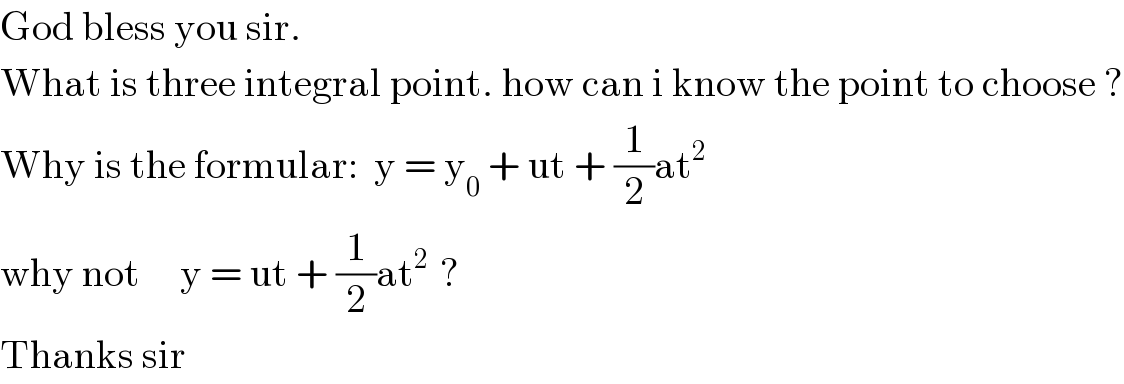
God bless you sir. What is three integral point. how can i know the point to choose ? Why is the formular: y = y_0 + ut + (1/2)at^2 why not y = ut + (1/2)at^(2 ) ? Thanks sir
$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}.\:\: \\ $$$$\mathrm{What}\:\mathrm{is}\:\mathrm{three}\:\mathrm{integral}\:\mathrm{point}.\:\mathrm{how}\:\mathrm{can}\:\mathrm{i}\:\mathrm{know}\:\mathrm{the}\:\mathrm{point}\:\mathrm{to}\:\mathrm{choose}\:? \\ $$$$\mathrm{Why}\:\mathrm{is}\:\mathrm{the}\:\mathrm{formular}:\:\:\mathrm{y}\:=\:\mathrm{y}_{\mathrm{0}} \:+\:\mathrm{ut}\:+\:\frac{\mathrm{1}}{\mathrm{2}}\mathrm{at}^{\mathrm{2}} \: \\ $$$$\mathrm{why}\:\mathrm{not}\:\:\:\:\:\mathrm{y}\:=\:\mathrm{ut}\:+\:\frac{\mathrm{1}}{\mathrm{2}}\mathrm{at}^{\mathrm{2}\:\:\:} ? \\ $$$$\mathrm{Thanks}\:\mathrm{sir} \\ $$
Commented by tawa tawa last updated on 09/Feb/18
And sir. What are the answers to the question. look like you are not through with the workings sir. Thanks for your help. waiting for the solution to the question. (i), (ii), (iii)
$$\mathrm{And}\:\mathrm{sir}.\:\:\mathrm{What}\:\mathrm{are}\:\mathrm{the}\:\mathrm{answers}\:\mathrm{to}\:\mathrm{the}\:\mathrm{question}.\:\:\mathrm{look}\:\mathrm{like}\:\mathrm{you}\:\mathrm{are}\:\mathrm{not} \\ $$$$\mathrm{through}\:\mathrm{with}\:\mathrm{the}\:\mathrm{workings}\:\mathrm{sir}.\:\:\mathrm{Thanks}\:\mathrm{for}\:\mathrm{your}\:\mathrm{help}. \\ $$$$\mathrm{waiting}\:\mathrm{for}\:\mathrm{the}\:\mathrm{solution}\:\mathrm{to}\:\mathrm{the}\:\mathrm{question}.\:\:\left(\mathrm{i}\right),\:\:\left(\mathrm{ii}\right),\:\:\left(\mathrm{iii}\right) \\ $$
Commented by 33 last updated on 10/Feb/18
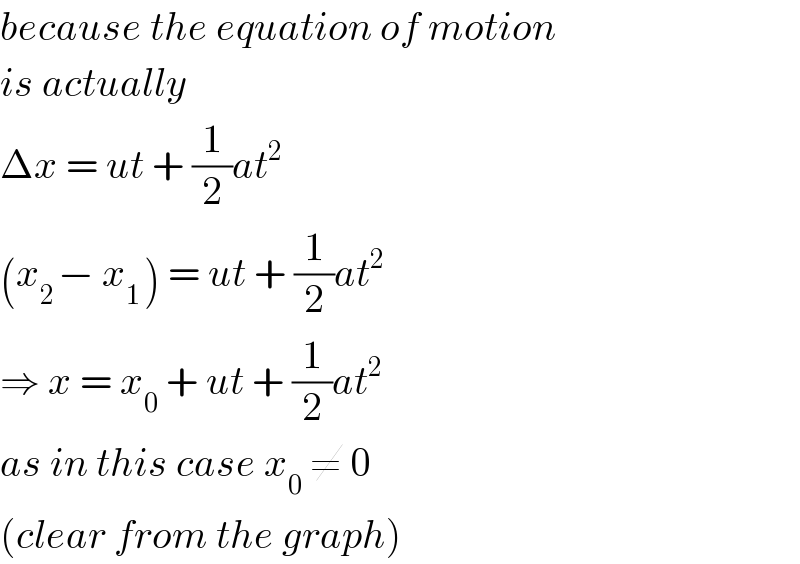
because the equation of motion is actually Δx = ut + (1/2)at^2 (x_(2 ) − x_(1 ) ) = ut + (1/2)at^2 ⇒ x = x_0 + ut + (1/2)at^2 as in this case x_0 ≠ 0 (clear from the graph)
$${because}\:{the}\:{equation}\:{of}\:{motion} \\ $$$${is}\:{actually}\: \\ $$$$\Delta{x}\:=\:{ut}\:+\:\frac{\mathrm{1}}{\mathrm{2}}{at}^{\mathrm{2}} \\ $$$$\left({x}_{\mathrm{2}\:} −\:{x}_{\mathrm{1}\:} \right)\:=\:{ut}\:+\:\frac{\mathrm{1}}{\mathrm{2}}{at}^{\mathrm{2}} \\ $$$$\Rightarrow\:{x}\:=\:{x}_{\mathrm{0}} \:+\:{ut}\:+\:\frac{\mathrm{1}}{\mathrm{2}}{at}^{\mathrm{2}} \\ $$$${as}\:{in}\:{this}\:{case}\:{x}_{\mathrm{0}} \:\neq\:\mathrm{0}\: \\ $$$$\left({clear}\:{from}\:{the}\:{graph}\right) \\ $$
Commented by tawa tawa last updated on 10/Feb/18
Understood sir. God bless you
$$\mathrm{Understood}\:\mathrm{sir}.\:\mathrm{God}\:\mathrm{bless}\:\mathrm{you} \\ $$
Commented by tawa tawa last updated on 10/Feb/18
And please sir. how is distance travel in 2s = y_1 − y_0 + y_1
$$\mathrm{And}\:\mathrm{please}\:\mathrm{sir}.\:\mathrm{how}\:\mathrm{is}\:\mathrm{distance}\:\mathrm{travel}\:\mathrm{in}\:\:\mathrm{2s}\:\:=\:\:\mathrm{y}_{\mathrm{1}} \:−\:\mathrm{y}_{\mathrm{0}} \:+\:\mathrm{y}_{\mathrm{1}} \\ $$
Commented by 33 last updated on 10/Feb/18
pls see the graph its clear
$${pls}\:{see}\:{the}\:{graph}\:{its}\:{clear} \\ $$
Commented by tawa tawa last updated on 10/Feb/18
Ummm. where sir ???
$$\mathrm{Ummm}.\:\mathrm{where}\:\mathrm{sir}\:\:??? \\ $$
Commented by ajfour last updated on 10/Feb/18
the graph in your question, i think, is meant.
$${the}\:{graph}\:{in}\:{your}\:{question},\:{i}\:{think}, \\ $$$${is}\:{meant}. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *