Menu Close

Question-29559

Tinku Tara 0 Comments
Pin




Question Number 29559 by ajfour last updated on 09/Feb/18
Commented by ajfour last updated on 10/Feb/18
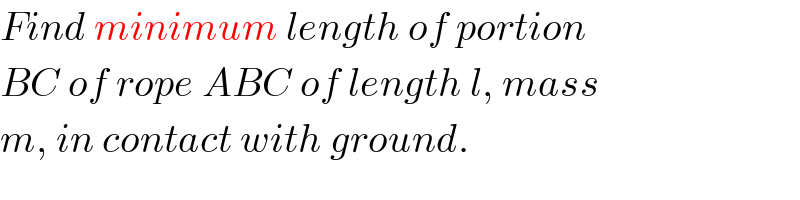
Find minimum length of portion BC of rope ABC of length l, mass m, in contact with ground.
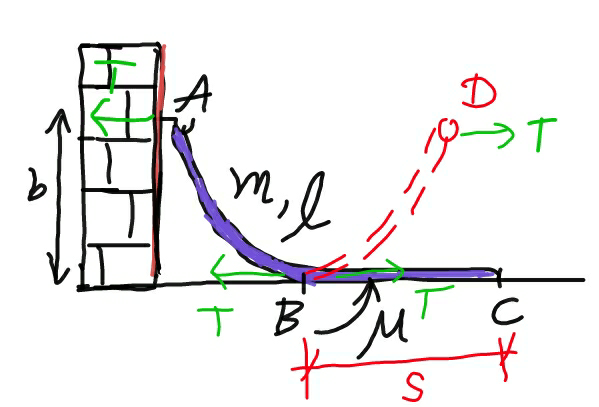
$${Find}\:{minimum}\:{length}\:{of}\:{portion} \\ $$$${BC}\:{of}\:{rope}\:{ABC}\:{of}\:{length}\:{l},\:{mass} \\ $$$${m},\:{in}\:{contact}\:{with}\:{ground}. \\ $$
Commented by ajfour last updated on 10/Feb/18
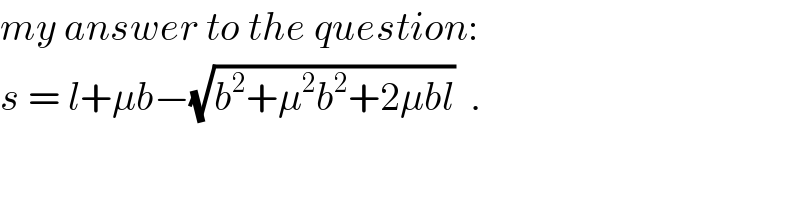
my answer to the question: s = l+μb−(√(b^2 +μ^2 b^2 +2μbl)) .
$${my}\:{answer}\:{to}\:{the}\:{question}: \\ $$$${s}\:=\:{l}+\mu{b}−\sqrt{{b}^{\mathrm{2}} +\mu^{\mathrm{2}} {b}^{\mathrm{2}} +\mathrm{2}\mu{bl}}\:\:. \\ $$
Commented by ajfour last updated on 10/Feb/18
Commented by ajfour last updated on 10/Feb/18
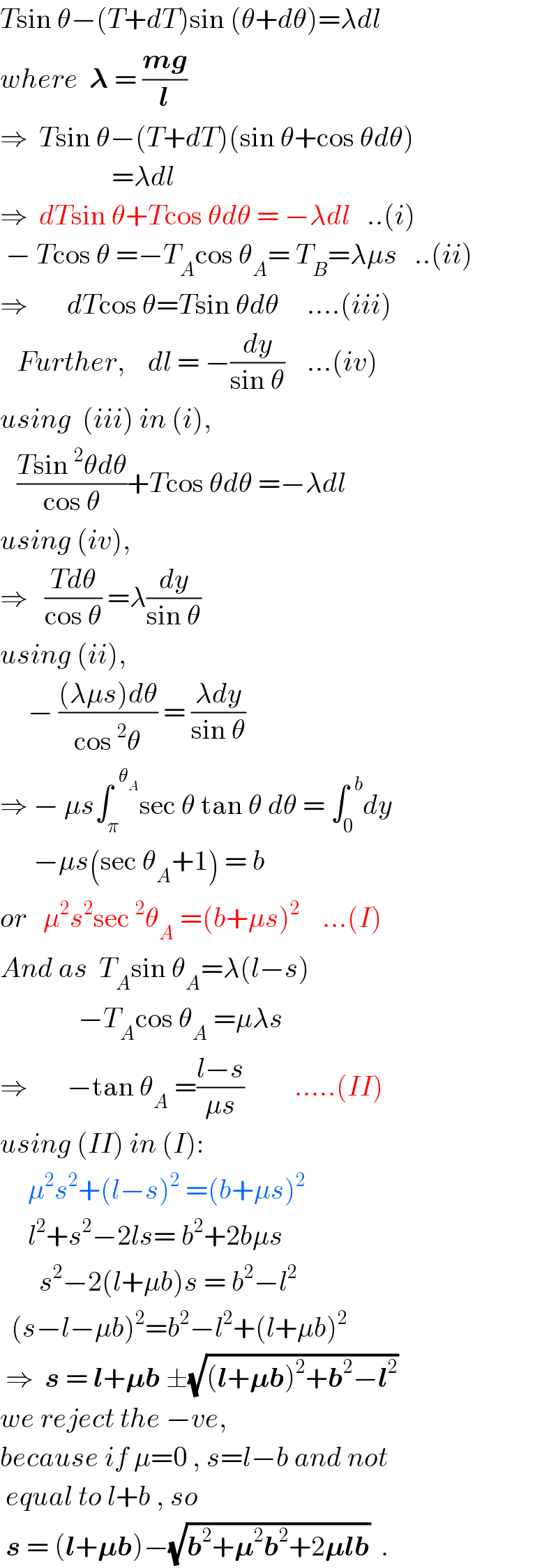
Tsin θ−(T+dT)sin (θ+dθ)=λdl where 𝛌 = ((mg)/l) ⇒ Tsin θ−(T+dT)(sin θ+cos θdθ) =λdl ⇒ dTsin θ+Tcos θdθ = −λdl ..(i) − Tcos θ =−T_A cos θ_A = T_B =λμs ..(ii) ⇒ dTcos θ=Tsin θdθ ....(iii) Further, dl = −(dy/(sin θ)) ...(iv) using (iii) in (i), ((Tsin^2 θdθ)/(cos θ))+Tcos θdθ =−λdl using (iv), ⇒ ((Tdθ)/(cos θ)) =λ(dy/(sin θ)) using (ii), − (((λμs)dθ)/(cos^2 θ)) = ((λdy)/(sin θ)) ⇒ − μs∫_π ^( θ_A ) sec θ tan θ dθ = ∫_0 ^( b) dy −μs(sec θ_A +1) = b or μ^2 s^2 sec^2 θ_A =(b+μs)^2 ...(I) And as T_A sin θ_A =λ(l−s) −T_A cos θ_A =μλs ⇒ −tan θ_A =((l−s)/(μs)) .....(II) using (II) in (I): μ^2 s^2 +(l−s)^2 =(b+μs)^2 l^2 +s^2 −2ls= b^2 +2bμs s^2 −2(l+μb)s = b^2 −l^2 (s−l−μb)^2 =b^2 −l^2 +(l+μb)^2 ⇒ s = l+𝛍b ±(√((l+𝛍b)^2 +b^2 −l^2 )) we reject the −ve, because if μ=0 , s=l−b and not equal to l+b , so s = (l+𝛍b)−(√(b^2 +𝛍^2 b^2 +2𝛍lb)) .
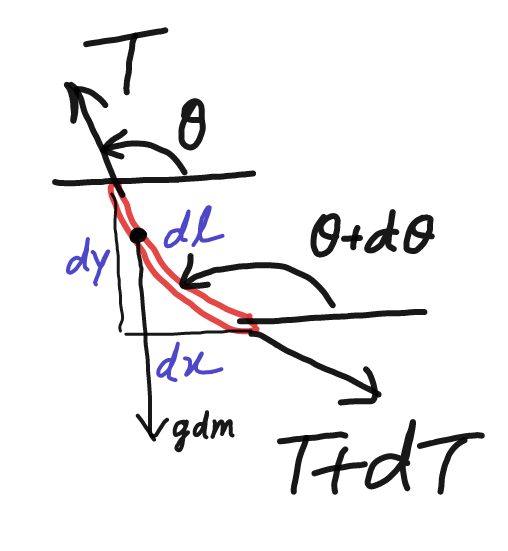
$${T}\mathrm{sin}\:\theta−\left({T}+{dT}\right)\mathrm{sin}\:\left(\theta+{d}\theta\right)=\lambda{dl} \\ $$$${where}\:\:\boldsymbol{\lambda}\:=\:\frac{\boldsymbol{{mg}}}{\boldsymbol{{l}}} \\ $$$$\Rightarrow\:\:{T}\mathrm{sin}\:\theta−\left({T}+{dT}\right)\left(\mathrm{sin}\:\theta+\mathrm{cos}\:\theta{d}\theta\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\lambda{dl}\:\:\:\:\:\:\:\:\: \\ $$$$\Rightarrow\:\:{dT}\mathrm{sin}\:\theta+{T}\mathrm{cos}\:\theta{d}\theta\:=\:−\lambda{dl}\:\:\:..\left({i}\right) \\ $$$$\:−\:{T}\mathrm{cos}\:\theta\:=−{T}_{{A}} \mathrm{cos}\:\theta_{{A}} =\:{T}_{{B}} =\lambda\mu{s}\:\:\:..\left({ii}\right) \\ $$$$\Rightarrow\:\:\:\:\:\:\:{dT}\mathrm{cos}\:\theta={T}\mathrm{sin}\:\theta{d}\theta\:\:\:\:\:….\left({iii}\right) \\ $$$$\:\:\:{Further},\:\:\:\:{dl}\:=\:−\frac{{dy}}{\mathrm{sin}\:\theta}\:\:\:\:…\left({iv}\right) \\ $$$${using}\:\:\left({iii}\right)\:{in}\:\left({i}\right), \\ $$$$\:\:\:\frac{{T}\mathrm{sin}\:^{\mathrm{2}} \theta{d}\theta}{\mathrm{cos}\:\theta}+{T}\mathrm{cos}\:\theta{d}\theta\:=−\lambda{dl} \\ $$$${using}\:\left({iv}\right), \\ $$$$\Rightarrow\:\:\:\frac{{Td}\theta}{\mathrm{cos}\:\theta}\:=\lambda\frac{{dy}}{\mathrm{sin}\:\theta} \\ $$$${using}\:\left({ii}\right), \\ $$$$\:\:\:\:\:−\:\frac{\left(\lambda\mu{s}\right){d}\theta}{\mathrm{cos}\:^{\mathrm{2}} \theta}\:=\:\frac{\lambda{dy}}{\mathrm{sin}\:\theta} \\ $$$$\Rightarrow\:−\:\mu{s}\int_{\pi} ^{\:\:\theta_{{A}} } \mathrm{sec}\:\theta\:\mathrm{tan}\:\theta\:{d}\theta\:=\:\int_{\mathrm{0}} ^{\:\:{b}} {dy} \\ $$$$\:\:\:\:\:\:−\mu{s}\left(\mathrm{sec}\:\theta_{{A}} +\mathrm{1}\right)\:=\:{b} \\ $$$${or}\:\:\:\mu^{\mathrm{2}} {s}^{\mathrm{2}} \mathrm{sec}\:^{\mathrm{2}} \theta_{{A}} \:=\left({b}+\mu{s}\right)^{\mathrm{2}} \:\:\:\:…\left({I}\right) \\ $$$${And}\:{as}\:\:{T}_{{A}} \mathrm{sin}\:\theta_{{A}} =\lambda\left({l}−{s}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:−{T}_{{A}} \mathrm{cos}\:\theta_{{A}} \:=\mu\lambda{s} \\ $$$$\Rightarrow\:\:\:\:\:\:\:−\mathrm{tan}\:\theta_{{A}} \:=\frac{{l}−{s}}{\mu{s}}\:\:\:\:\:\:\:\:\:…..\left({II}\right) \\ $$$${using}\:\left({II}\right)\:{in}\:\left({I}\right): \\ $$$$\:\:\:\:\:\mu^{\mathrm{2}} {s}^{\mathrm{2}} +\left({l}−{s}\right)^{\mathrm{2}} \:=\left({b}+\mu{s}\right)^{\mathrm{2}} \\ $$$$\:\:\:\:\:{l}^{\mathrm{2}} +{s}^{\mathrm{2}} −\mathrm{2}{ls}=\:{b}^{\mathrm{2}} +\mathrm{2}{b}\mu{s} \\ $$$$\:\:\:\:\:\:\:{s}^{\mathrm{2}} −\mathrm{2}\left({l}+\mu{b}\right){s}\:=\:{b}^{\mathrm{2}} −{l}^{\mathrm{2}} \\ $$$$\:\:\left({s}−{l}−\mu{b}\right)^{\mathrm{2}} ={b}^{\mathrm{2}} −{l}^{\mathrm{2}} +\left({l}+\mu{b}\right)^{\mathrm{2}} \\ $$$$\:\Rightarrow\:\:\boldsymbol{{s}}\:=\:\boldsymbol{{l}}+\boldsymbol{\mu{b}}\:\pm\sqrt{\left(\boldsymbol{{l}}+\boldsymbol{\mu{b}}\right)^{\mathrm{2}} +\boldsymbol{{b}}^{\mathrm{2}} −\boldsymbol{{l}}^{\mathrm{2}} } \\ $$$${we}\:{reject}\:{the}\:−{ve},\: \\ $$$${because}\:{if}\:\mu=\mathrm{0}\:,\:{s}={l}−{b}\:{and}\:{not} \\ $$$$\:{equal}\:{to}\:{l}+{b}\:,\:{so} \\ $$$$\:\boldsymbol{{s}}\:=\:\left(\boldsymbol{{l}}+\boldsymbol{\mu{b}}\right)−\sqrt{\boldsymbol{{b}}^{\mathrm{2}} +\boldsymbol{\mu}^{\mathrm{2}} \boldsymbol{{b}}^{\mathrm{2}} +\mathrm{2}\boldsymbol{\mu{lb}}}\:\:. \\ $$
Commented by ajfour last updated on 10/Feb/18
anything wrong with my method ? Please check my solution mrW Sir.
$${anything}\:{wrong}\:{with}\:{my}\:{method}\:? \\ $$$${Please}\:{check}\:{my}\:{solution} \\ $$$${mrW}\:{Sir}. \\ $$
Commented by mrW2 last updated on 10/Feb/18
Your answer is correct sir. I made a mistake in my calculation.
$${Your}\:{answer}\:{is}\:{correct}\:{sir}.\: \\ $$$${I}\:{made}\:{a}\:{mistake}\:{in}\:{my}\:{calculation}. \\ $$
Answered by mrW2 last updated on 10/Feb/18
Commented by 33 last updated on 10/Feb/18
Sir, we can also use the equation of caternary arc. i dont know much about it tho. just suggesting
$${Sir},\:{we}\:{can}\:{also}\:{use}\:{the}\:{equation} \\ $$$${of}\:{caternary}\:{arc}.\:{i}\:{dont}\:{know} \\ $$$${much}\:{about}\:{it}\:{tho}.\:{just}\:{suggesting} \\ $$
Commented by 33 last updated on 10/Feb/18
glad that my suggestion helped you
$${glad}\:{that}\:{my}\:{suggestion}\:{helped}\:{you} \\ $$
Commented by mrW2 last updated on 10/Feb/18
let ρ=(m/l) let′s say the length of portion BC is s. then length of portion AB=l−s length of imaged rope AD=2(l−s) the tension in rope AD at B is T T≤μρsg (=max. friction force) now we look at the catenary ABD. eqn. of catenary is y=a cosh (x/a) L=a sinh (x/a) (length of rope upon B) with a=(T/(ρg))=((μρsg)/(ρg))=μs assume distance from A to D=2λa at point D we have: y=a+b=a cosh ((λa)/a) ⇒cosh λ=((a+b)/a) ..(i) l−s=a sinh ((λa)/a) ⇒sinh λ=((l−s)/a) ..(ii) cosh^2 λ−sinh^2 λ=1 ⇒(((a+b)/a))^2 −(((l−s)/a))^2 =1 ⇒a^2 +2ab+b^2 −l^2 +2ls−s^2 =a^2 ⇒2ab+b^2 −l^2 +2ls−s^2 =0 ⇒2μbs+b^2 −l^2 +2ls−s^2 =0 ⇒s^2 −2(l+μb)s+l^2 −b^2 =0 ⇒s=(l+μb)−(√((l+μb)^2 −(l^2 −b^2 ))) (+(√(...)) is not suitable) ⇒s=(l+μb)−(√((1+μ^2 )b^2 +2μbl))
$${let}\:\rho=\frac{{m}}{{l}} \\ $$$${let}'{s}\:{say}\:{the}\:{length}\:{of}\:{portion}\:{BC}\:{is}\:{s}. \\ $$$${then}\:{length}\:{of}\:{portion}\:{AB}={l}−{s} \\ $$$${length}\:{of}\:{imaged}\:{rope}\:{AD}=\mathrm{2}\left({l}−{s}\right) \\ $$$${the}\:{tension}\:{in}\:{rope}\:{AD}\:{at}\:{B}\:{is}\:{T} \\ $$$${T}\leqslant\mu\rho{sg}\:\left(={max}.\:{friction}\:{force}\right) \\ $$$$ \\ $$$${now}\:{we}\:{look}\:{at}\:{the}\:{catenary}\:{ABD}. \\ $$$${eqn}.\:{of}\:{catenary}\:{is} \\ $$$${y}={a}\:\mathrm{cosh}\:\frac{{x}}{{a}} \\ $$$${L}={a}\:\mathrm{sinh}\:\frac{{x}}{{a}}\:\left({length}\:{of}\:{rope}\:{upon}\:{B}\right) \\ $$$${with}\:{a}=\frac{{T}}{\rho{g}}=\frac{\mu\rho{sg}}{\rho{g}}=\mu{s} \\ $$$$ \\ $$$${assume}\:{distance}\:{from}\:{A}\:{to}\:{D}=\mathrm{2}\lambda{a} \\ $$$$ \\ $$$${at}\:{point}\:{D}\:{we}\:{have}: \\ $$$${y}={a}+{b}={a}\:\mathrm{cosh}\:\frac{\lambda{a}}{{a}} \\ $$$$\Rightarrow\mathrm{cosh}\:\lambda=\frac{{a}+{b}}{{a}}\:\:\:..\left({i}\right) \\ $$$${l}−{s}={a}\:\mathrm{sinh}\:\frac{\lambda{a}}{{a}} \\ $$$$\Rightarrow\mathrm{sinh}\:\lambda=\frac{{l}−{s}}{{a}}\:\:\:\:..\left({ii}\right) \\ $$$$ \\ $$$$\mathrm{cosh}^{\mathrm{2}} \:\lambda−\mathrm{sinh}^{\mathrm{2}} \:\lambda=\mathrm{1} \\ $$$$\Rightarrow\left(\frac{{a}+{b}}{{a}}\right)^{\mathrm{2}} −\left(\frac{{l}−{s}}{{a}}\right)^{\mathrm{2}} =\mathrm{1} \\ $$$$\Rightarrow{a}^{\mathrm{2}} +\mathrm{2}{ab}+{b}^{\mathrm{2}} −{l}^{\mathrm{2}} +\mathrm{2}{ls}−{s}^{\mathrm{2}} ={a}^{\mathrm{2}} \\ $$$$\Rightarrow\mathrm{2}{ab}+{b}^{\mathrm{2}} −{l}^{\mathrm{2}} +\mathrm{2}{ls}−{s}^{\mathrm{2}} =\mathrm{0} \\ $$$$\Rightarrow\mathrm{2}\mu{bs}+{b}^{\mathrm{2}} −{l}^{\mathrm{2}} +\mathrm{2}{ls}−{s}^{\mathrm{2}} =\mathrm{0} \\ $$$$\Rightarrow{s}^{\mathrm{2}} −\mathrm{2}\left({l}+\mu{b}\right){s}+{l}^{\mathrm{2}} −{b}^{\mathrm{2}} =\mathrm{0} \\ $$$$\Rightarrow{s}=\left({l}+\mu{b}\right)−\sqrt{\left({l}+\mu{b}\right)^{\mathrm{2}} −\left({l}^{\mathrm{2}} −{b}^{\mathrm{2}} \right)}\:\:\left(+\sqrt{…}\:{is}\:{not}\:{suitable}\right) \\ $$$$\Rightarrow{s}=\left({l}+\mu{b}\right)−\sqrt{\left(\mathrm{1}+\mu^{\mathrm{2}} \right){b}^{\mathrm{2}} +\mathrm{2}\mu{bl}} \\ $$
Commented by mrW2 last updated on 10/Feb/18
To 33 sir: yes. the application of catenary eqn. in this case is suitable.
$${To}\:\mathrm{33}\:{sir}: \\ $$$${yes}.\:{the}\:{application}\:{of}\:{catenary}\:{eqn}. \\ $$$${in}\:{this}\:{case}\:{is}\:{suitable}. \\ $$
Commented by ajfour last updated on 11/Feb/18
Thanks Sir, but i guess, i will need time and effort to follow (this catenary thing).
$${Thanks}\:{Sir},\:{but}\:{i}\:{guess},\:{i}\:{will}\:{need}\:{time} \\ $$$${and}\:{effort}\:{to}\:{follow}\:\left({this}\:{catenary}\right. \\ $$$$\left.{thing}\right). \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *