Question Number 29687 by ajfour last updated on 11/Feb/18
Commented by ajfour last updated on 11/Feb/18

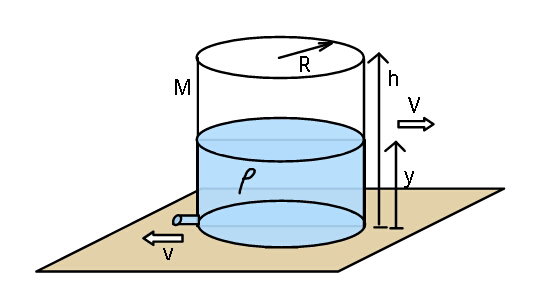
$${Find}\:{the}\:{final}\:{velocity}\:{gained}\:{by}\:{a} \\ $$$${tank}\:{of}\:{mass}\:{M},\:{initially}\:{completely} \\ $$$${filled}\:{with}\:{water}\:{and}\:{at}\:{rest},\:{as}\:{it} \\ $$$${slips}\:{on}\:{a}\:{frictionless}\:{ground}\:{owing} \\ $$$${to}\:{a}\:{small}\:{opening}\:{at}\:{its}\:{base}\:{of} \\ $$$${radius}\:{a},\:{through}\:{which}\:{it}\:{drains} \\ $$$${out}.\:\left({Assume}\:{density}\:{of}\:{water}\:\boldsymbol{\rho}\right). \\ $$
Commented by 803jaideep@gmail.com last updated on 11/Feb/18
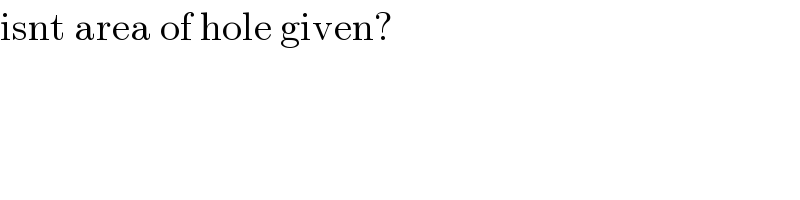
$$\mathrm{isnt}\:\mathrm{area}\:\mathrm{of}\:\mathrm{hole}\:\mathrm{given}? \\ $$
Commented by ajfour last updated on 11/Feb/18
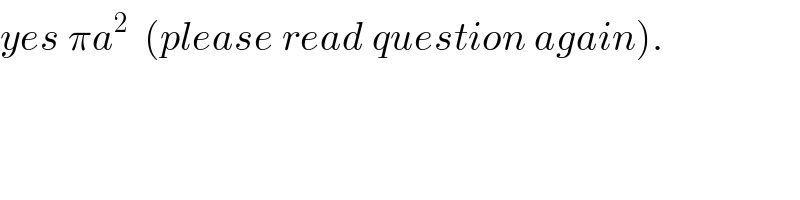
$${yes}\:\pi{a}^{\mathrm{2}} \:\:\left({please}\:{read}\:{question}\:{again}\right). \\ $$
Commented by ajfour last updated on 11/Feb/18
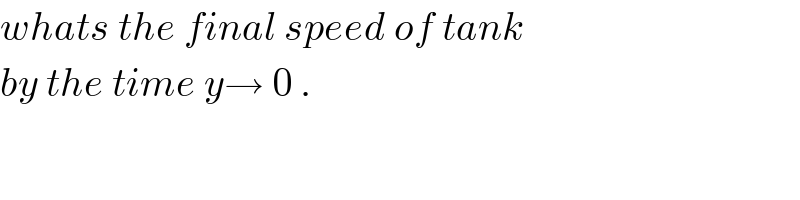
$${whats}\:{the}\:{final}\:{speed}\:{of}\:{tank} \\ $$$${by}\:{the}\:{time}\:{y}\rightarrow\:\mathrm{0}\:. \\ $$
Answered by mrW2 last updated on 12/Feb/18
![M_W =mass of water at begin=πR^2 hρ at water depth y: total mass: m=M+M_W (y/h) ⇒(dm/dt)=(M_W /h)×(dy/dt) (relative) speed of outgoing water: v=(√(2gy)) let′s say speed of tank=u −v(dm/dt)=m(du/dt) −v×(M_W /h)×(dy/dt)=m(du/dy)×(dy/dt) −(M_W /h)v=m(du/dy) −(M_W /h)(√(2gy))=(M+(M_W /h)y)(du/dy) −(M_W /h)×((√(2gy))/(M+(M_W /h)y)) dy=du −(√(2g))×((√y)/((((hM)/M_W )+y))) dy=du with k=((hM)/M_W ) −(√(2g))×∫_h ^( 0) ((√y)/((k+y))) dy=∫_0 ^( u_(max) ) du (√(2g))×2(√k)[(√(y/k))−tan^(−1) (√(y/k))]_0 ^h =u_(max) u_(max) =2(√(2gk))((√(h/k))−tan^(−1) (√(h/k))) u_(max) =2(√((2ghM)/M_W ))((√(M_W /M))−tan^(−1) (√(M_W /M))) with λ=(M_W /M) ⇒u_(max) =2(√((2gh)/λ))((√λ)−tan^(−1) (√λ)) Example: λ=(M_W /M)=5, h=1 m ⇒u_(max) =2(√((20)/5))((√5)−tan^(−1) (√5))=4.3 m/s ==================== u(y)=2(√(2gk))((√(h/k))−(√(y/k))−tan^(−1) (√(h/k))+tan^(−1) (√(y/k))) πa^2 vdt=−πR^2 dy ⇒(dy/dt)=−(a^2 /R^2 )v=−((a^2 (√(2gy)))/R^2 ) ⇒(dy/( (√y)))=−((a^2 (√(2g)))/R^2 ) dt ⇒∫_h ^( y) (dy/( (√y)))=−((a^2 (√(2g)))/R^2 ) ∫_0 ^( t) dt ⇒2((√y)−(√h))=−((a^2 (√(2g)))/R^2 )×t ⇒(√y)=(√h)−((a^2 (√(2g)))/(2R^2 ))×t=(√h)−pt ⇒y=h−2(√h)pt+p^2 t^2 y=0⇒t=((√h)/p)=(R^2 /a^2 )(√((2h)/g))=t_1 (at t_1 tank is empty) ⇒u(t)=2(√(2gk))[((pt)/( (√k)))−tan^(−1) (√(h/k))+tan^(−1) ((√(h/k))−((pt)/( (√k))))] with η=(p/( (√k)))=(a^2 /R^2 )(√((2gλ)/h)) ⇒u(t)=2(√((2gh)/λ))[ηt−tan^(−1) (√λ)+tan^(−1) ((√λ)−ηt)]](https://www.tinkutara.com/question/Q29759.png)
$${M}_{{W}} ={mass}\:{of}\:{water}\:{at}\:{begin}=\pi{R}^{\mathrm{2}} {h}\rho \\ $$$${at}\:{water}\:{depth}\:{y}: \\ $$$${total}\:{mass}:\:{m}={M}+{M}_{{W}} \frac{{y}}{{h}} \\ $$$$\Rightarrow\frac{{dm}}{{dt}}=\frac{{M}_{{W}} }{{h}}×\frac{{dy}}{{dt}} \\ $$$$\left({relative}\right)\:{speed}\:{of}\:{outgoing}\:{water}: \\ $$$${v}=\sqrt{\mathrm{2}{gy}} \\ $$$$ \\ $$$${let}'{s}\:{say}\:{speed}\:{of}\:{tank}={u} \\ $$$$−{v}\frac{{dm}}{{dt}}={m}\frac{{du}}{{dt}} \\ $$$$−{v}×\frac{{M}_{{W}} }{{h}}×\frac{{dy}}{{dt}}={m}\frac{{du}}{{dy}}×\frac{{dy}}{{dt}} \\ $$$$−\frac{{M}_{{W}} }{{h}}{v}={m}\frac{{du}}{{dy}} \\ $$$$−\frac{{M}_{{W}} }{{h}}\sqrt{\mathrm{2}{gy}}=\left({M}+\frac{{M}_{{W}} }{{h}}{y}\right)\frac{{du}}{{dy}} \\ $$$$−\frac{{M}_{{W}} }{{h}}×\frac{\sqrt{\mathrm{2}{gy}}}{{M}+\frac{{M}_{{W}} }{{h}}{y}}\:{dy}={du} \\ $$$$−\sqrt{\mathrm{2}{g}}×\frac{\sqrt{{y}}}{\left(\frac{{hM}}{{M}_{{W}} }+{y}\right)}\:{dy}={du} \\ $$$${with}\:{k}=\frac{{hM}}{{M}_{{W}} } \\ $$$$−\sqrt{\mathrm{2}{g}}×\int_{{h}} ^{\:\mathrm{0}} \frac{\sqrt{{y}}}{\left({k}+{y}\right)}\:{dy}=\int_{\mathrm{0}} ^{\:{u}_{{max}} } {du} \\ $$$$\sqrt{\mathrm{2}{g}}×\mathrm{2}\sqrt{{k}}\left[\sqrt{\frac{{y}}{{k}}}−\mathrm{tan}^{−\mathrm{1}} \sqrt{\frac{{y}}{{k}}}\right]_{\mathrm{0}} ^{{h}} ={u}_{{max}} \\ $$$${u}_{{max}} =\mathrm{2}\sqrt{\mathrm{2}{gk}}\left(\sqrt{\frac{{h}}{{k}}}−\mathrm{tan}^{−\mathrm{1}} \sqrt{\frac{{h}}{{k}}}\right) \\ $$$${u}_{{max}} =\mathrm{2}\sqrt{\frac{\mathrm{2}{ghM}}{{M}_{{W}} }}\left(\sqrt{\frac{{M}_{{W}} }{{M}}}−\mathrm{tan}^{−\mathrm{1}} \sqrt{\frac{{M}_{{W}} }{{M}}}\right) \\ $$$${with}\:\lambda=\frac{{M}_{{W}} }{{M}} \\ $$$$\Rightarrow{u}_{{max}} =\mathrm{2}\sqrt{\frac{\mathrm{2}{gh}}{\lambda}}\left(\sqrt{\lambda}−\mathrm{tan}^{−\mathrm{1}} \sqrt{\lambda}\right) \\ $$$$ \\ $$$${Example}:\:\lambda=\frac{{M}_{{W}} }{{M}}=\mathrm{5},\:{h}=\mathrm{1}\:{m} \\ $$$$\Rightarrow{u}_{{max}} =\mathrm{2}\sqrt{\frac{\mathrm{20}}{\mathrm{5}}}\left(\sqrt{\mathrm{5}}−\mathrm{tan}^{−\mathrm{1}} \sqrt{\mathrm{5}}\right)=\mathrm{4}.\mathrm{3}\:{m}/{s} \\ $$$$==================== \\ $$$${u}\left({y}\right)=\mathrm{2}\sqrt{\mathrm{2}{gk}}\left(\sqrt{\frac{{h}}{{k}}}−\sqrt{\frac{{y}}{{k}}}−\mathrm{tan}^{−\mathrm{1}} \sqrt{\frac{{h}}{{k}}}+\mathrm{tan}^{−\mathrm{1}} \sqrt{\frac{{y}}{{k}}}\right) \\ $$$$\pi{a}^{\mathrm{2}} {vdt}=−\pi{R}^{\mathrm{2}} {dy} \\ $$$$\Rightarrow\frac{{dy}}{{dt}}=−\frac{{a}^{\mathrm{2}} }{{R}^{\mathrm{2}} }{v}=−\frac{{a}^{\mathrm{2}} \sqrt{\mathrm{2}{gy}}}{{R}^{\mathrm{2}} } \\ $$$$\Rightarrow\frac{{dy}}{\:\sqrt{{y}}}=−\frac{{a}^{\mathrm{2}} \sqrt{\mathrm{2}{g}}}{{R}^{\mathrm{2}} }\:{dt} \\ $$$$\Rightarrow\int_{{h}} ^{\:{y}} \frac{{dy}}{\:\sqrt{{y}}}=−\frac{{a}^{\mathrm{2}} \sqrt{\mathrm{2}{g}}}{{R}^{\mathrm{2}} }\:\int_{\mathrm{0}} ^{\:{t}} {dt} \\ $$$$\Rightarrow\mathrm{2}\left(\sqrt{{y}}−\sqrt{{h}}\right)=−\frac{{a}^{\mathrm{2}} \sqrt{\mathrm{2}{g}}}{{R}^{\mathrm{2}} }×{t} \\ $$$$\Rightarrow\sqrt{{y}}=\sqrt{{h}}−\frac{{a}^{\mathrm{2}} \sqrt{\mathrm{2}{g}}}{\mathrm{2}{R}^{\mathrm{2}} }×{t}=\sqrt{{h}}−{pt} \\ $$$$\Rightarrow{y}={h}−\mathrm{2}\sqrt{{h}}{pt}+{p}^{\mathrm{2}} {t}^{\mathrm{2}} \\ $$$${y}=\mathrm{0}\Rightarrow{t}=\frac{\sqrt{{h}}}{{p}}=\frac{{R}^{\mathrm{2}} }{{a}^{\mathrm{2}} }\sqrt{\frac{\mathrm{2}{h}}{{g}}}={t}_{\mathrm{1}} \:\left({at}\:{t}_{\mathrm{1}} \:{tank}\:{is}\:{empty}\right) \\ $$$$ \\ $$$$\Rightarrow{u}\left({t}\right)=\mathrm{2}\sqrt{\mathrm{2}{gk}}\left[\frac{{pt}}{\:\sqrt{{k}}}−\mathrm{tan}^{−\mathrm{1}} \sqrt{\frac{{h}}{{k}}}+\mathrm{tan}^{−\mathrm{1}} \left(\sqrt{\frac{{h}}{{k}}}−\frac{{pt}}{\:\sqrt{{k}}}\right)\right] \\ $$$${with}\:\eta=\frac{{p}}{\:\sqrt{{k}}}=\frac{{a}^{\mathrm{2}} }{{R}^{\mathrm{2}} }\sqrt{\frac{\mathrm{2}{g}\lambda}{{h}}} \\ $$$$\Rightarrow{u}\left({t}\right)=\mathrm{2}\sqrt{\frac{\mathrm{2}{gh}}{\lambda}}\left[\eta{t}−\mathrm{tan}^{−\mathrm{1}} \sqrt{\lambda}+\mathrm{tan}^{−\mathrm{1}} \left(\sqrt{\lambda}−\eta{t}\right)\right] \\ $$
Commented by mrW2 last updated on 12/Feb/18
Is any solution for this question given?
Commented by ajfour last updated on 12/Feb/18

$$\mathbb{SUPERB}!\:{Sir},\:{Energy}\:{method} \\ $$$${leads}\:{to}\:{a}\:{complicated}\:{differential} \\ $$$${equation},\:{i}\:{guess}.\: \\ $$$${Your}\:{method}\:{is}\:\mathscr{E}{xcellent}\:,\:{Sir}. \\ $$
Commented by ajfour last updated on 12/Feb/18
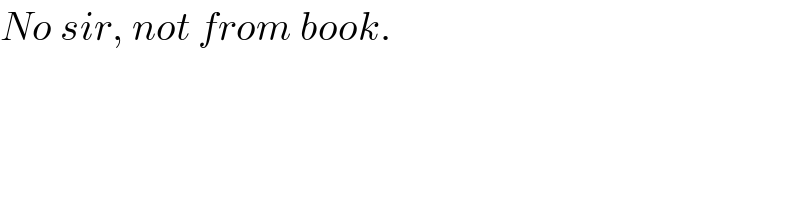
$${No}\:{sir},\:{not}\:{from}\:{book}. \\ $$
