Question Number 29723 by ajfour last updated on 11/Feb/18
Commented by ajfour last updated on 11/Feb/18
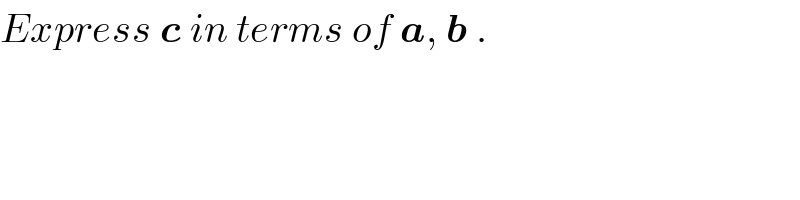
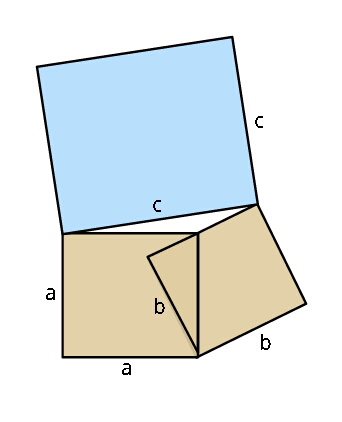
$${Express}\:\boldsymbol{{c}}\:{in}\:{terms}\:{of}\:\boldsymbol{{a}},\:\boldsymbol{{b}}\:. \\ $$
Answered by mrW2 last updated on 11/Feb/18
Commented by ajfour last updated on 12/Feb/18

$${Thank}\:{you}\:{Sir}. \\ $$
Commented by mrW2 last updated on 11/Feb/18
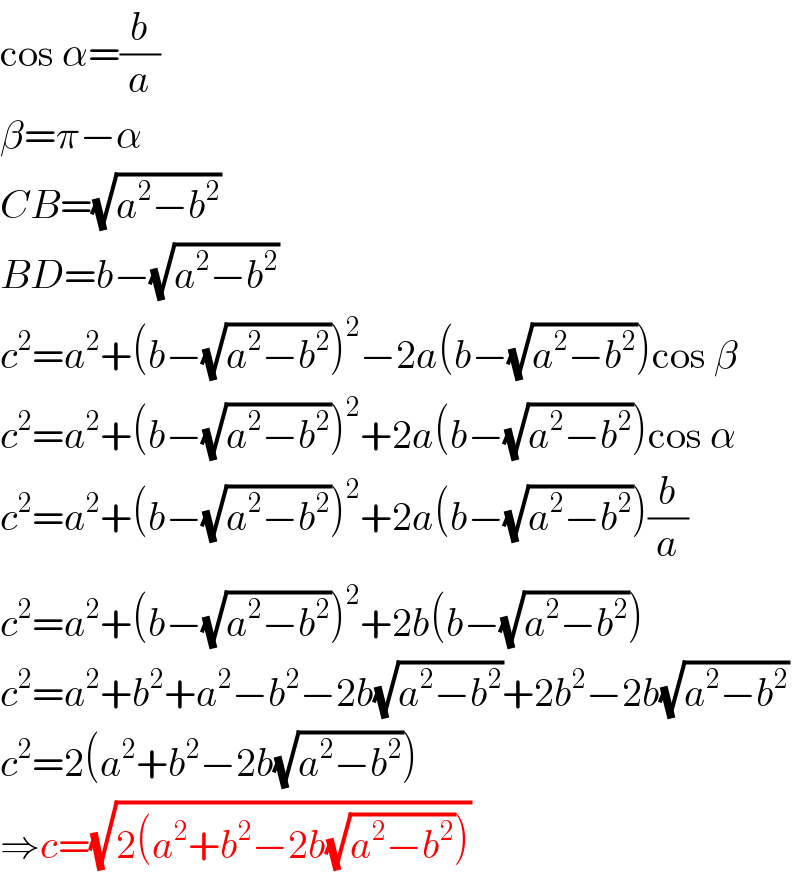
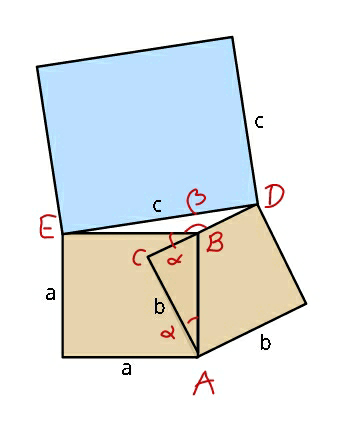
$$\mathrm{cos}\:\alpha=\frac{{b}}{{a}} \\ $$$$\beta=\pi−\alpha \\ $$$${CB}=\sqrt{{a}^{\mathrm{2}} −{b}^{\mathrm{2}} } \\ $$$${BD}={b}−\sqrt{{a}^{\mathrm{2}} −{b}^{\mathrm{2}} } \\ $$$${c}^{\mathrm{2}} ={a}^{\mathrm{2}} +\left({b}−\sqrt{{a}^{\mathrm{2}} −{b}^{\mathrm{2}} }\right)^{\mathrm{2}} −\mathrm{2}{a}\left({b}−\sqrt{{a}^{\mathrm{2}} −{b}^{\mathrm{2}} }\right)\mathrm{cos}\:\beta \\ $$$${c}^{\mathrm{2}} ={a}^{\mathrm{2}} +\left({b}−\sqrt{{a}^{\mathrm{2}} −{b}^{\mathrm{2}} }\right)^{\mathrm{2}} +\mathrm{2}{a}\left({b}−\sqrt{{a}^{\mathrm{2}} −{b}^{\mathrm{2}} }\right)\mathrm{cos}\:\alpha \\ $$$${c}^{\mathrm{2}} ={a}^{\mathrm{2}} +\left({b}−\sqrt{{a}^{\mathrm{2}} −{b}^{\mathrm{2}} }\right)^{\mathrm{2}} +\mathrm{2}{a}\left({b}−\sqrt{{a}^{\mathrm{2}} −{b}^{\mathrm{2}} }\right)\frac{{b}}{{a}} \\ $$$${c}^{\mathrm{2}} ={a}^{\mathrm{2}} +\left({b}−\sqrt{{a}^{\mathrm{2}} −{b}^{\mathrm{2}} }\right)^{\mathrm{2}} +\mathrm{2}{b}\left({b}−\sqrt{{a}^{\mathrm{2}} −{b}^{\mathrm{2}} }\right) \\ $$$${c}^{\mathrm{2}} ={a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{a}^{\mathrm{2}} −{b}^{\mathrm{2}} −\mathrm{2}{b}\sqrt{{a}^{\mathrm{2}} −{b}^{\mathrm{2}} }+\mathrm{2}{b}^{\mathrm{2}} −\mathrm{2}{b}\sqrt{{a}^{\mathrm{2}} −{b}^{\mathrm{2}} } \\ $$$${c}^{\mathrm{2}} =\mathrm{2}\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} −\mathrm{2}{b}\sqrt{{a}^{\mathrm{2}} −{b}^{\mathrm{2}} }\right) \\ $$$$\Rightarrow{c}=\sqrt{\mathrm{2}\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} −\mathrm{2}{b}\sqrt{{a}^{\mathrm{2}} −{b}^{\mathrm{2}} }\right)} \\ $$
