Question Number 29726 by naka3546 last updated on 11/Feb/18

Commented by ajfour last updated on 11/Feb/18
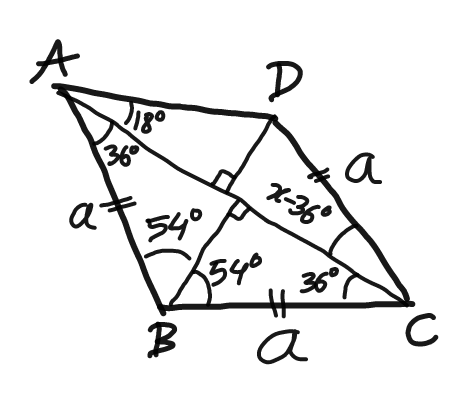
Commented by ajfour last updated on 12/Feb/18
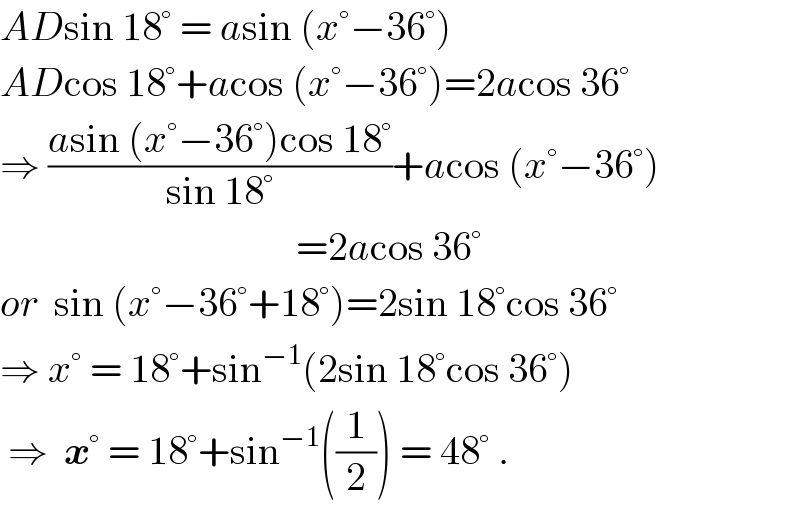
$${AD}\mathrm{sin}\:\mathrm{18}°\:=\:{a}\mathrm{sin}\:\left({x}°−\mathrm{36}°\right) \\ $$$${AD}\mathrm{cos}\:\mathrm{18}°+{a}\mathrm{cos}\:\left({x}°−\mathrm{36}°\right)=\mathrm{2}{a}\mathrm{cos}\:\mathrm{36}° \\ $$$$\Rightarrow\:\frac{{a}\mathrm{sin}\:\left({x}°−\mathrm{36}°\right)\mathrm{cos}\:\mathrm{18}°}{\mathrm{sin}\:\mathrm{18}°}+{a}\mathrm{cos}\:\left({x}°−\mathrm{36}°\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{2}{a}\mathrm{cos}\:\mathrm{36}° \\ $$$${or}\:\:\mathrm{sin}\:\left({x}°−\mathrm{36}°+\mathrm{18}°\right)=\mathrm{2sin}\:\mathrm{18}°\mathrm{cos}\:\mathrm{36}° \\ $$$$\Rightarrow\:{x}°\:=\:\mathrm{18}°+\mathrm{sin}^{−\mathrm{1}} \left(\mathrm{2sin}\:\mathrm{18}°\mathrm{cos}\:\mathrm{36}°\right)\: \\ $$$$\:\Rightarrow\:\:\boldsymbol{{x}}°\:=\:\mathrm{18}°+\mathrm{sin}^{−\mathrm{1}} \left(\frac{\mathrm{1}}{\mathrm{2}}\right)\:=\:\mathrm{48}°\:. \\ $$
