Question Number 29728 by rahul 19 last updated on 11/Feb/18

Commented by 803jaideep@gmail.com last updated on 11/Feb/18

$$\mathrm{i}\:\mathrm{dnt}\:\mathrm{know}\:\mathrm{exactly}\:\mathrm{but}\:\mathrm{i}\:\mathrm{think}\: \\ $$$$\mathrm{tangents}\:\mathrm{at}\:\mathrm{end}\:\mathrm{of}\:\mathrm{latus}\:\mathrm{rectum}\: \\ $$$$\mathrm{can}\:\mathrm{form}\:\mathrm{square} \\ $$
Commented by rahul 19 last updated on 11/Feb/18

Commented by rahul 19 last updated on 11/Feb/18
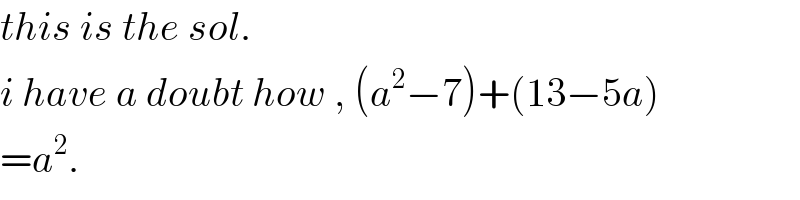
$${this}\:{is}\:{the}\:{sol}. \\ $$$${i}\:{have}\:{a}\:{doubt}\:{how}\:,\:\left({a}^{\mathrm{2}} −\mathrm{7}\right)+\left(\mathrm{13}−\mathrm{5}{a}\right) \\ $$$$={a}^{\mathrm{2}} . \\ $$
Commented by rahul 19 last updated on 11/Feb/18
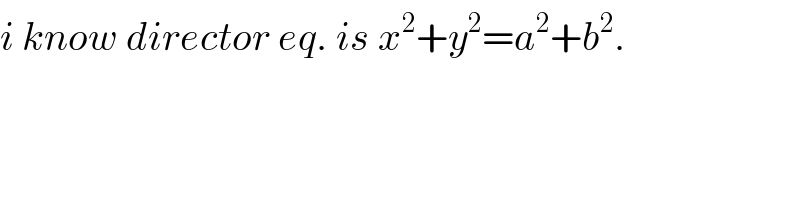
$${i}\:{know}\:{director}\:{eq}.\:{is}\:{x}^{\mathrm{2}} +{y}^{\mathrm{2}} ={a}^{\mathrm{2}} +{b}^{\mathrm{2}} . \\ $$
Commented by 803jaideep@gmail.com last updated on 11/Feb/18
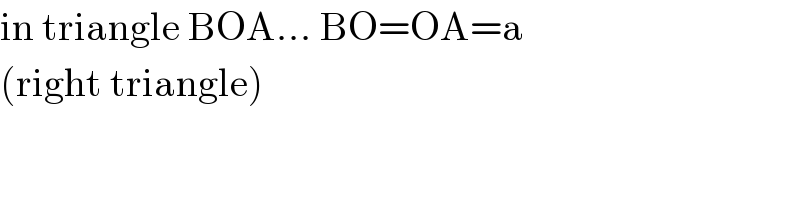
$$\mathrm{in}\:\mathrm{triangle}\:\mathrm{BOA}…\:\mathrm{BO}=\mathrm{OA}=\mathrm{a} \\ $$$$\left(\mathrm{right}\:\mathrm{triangle}\right) \\ $$
Commented by 803jaideep@gmail.com last updated on 11/Feb/18
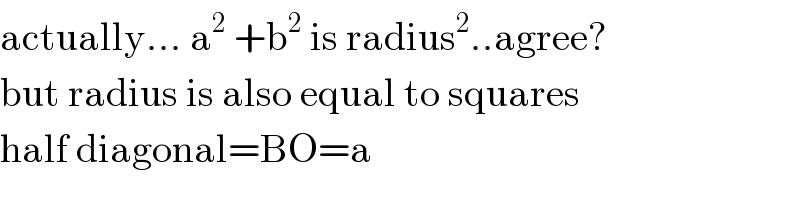
$$\mathrm{actually}…\:\mathrm{a}^{\mathrm{2}} \:+\mathrm{b}^{\mathrm{2}} \:\mathrm{is}\:\mathrm{radius}^{\mathrm{2}} ..\mathrm{agree}? \\ $$$$\mathrm{but}\:\mathrm{radius}\:\mathrm{is}\:\mathrm{also}\:\mathrm{equal}\:\mathrm{to}\:\mathrm{squares}\: \\ $$$$\mathrm{half}\:\mathrm{diagonal}=\mathrm{BO}=\mathrm{a} \\ $$
Commented by 803jaideep@gmail.com last updated on 11/Feb/18

$$\mathrm{it}\:\mathrm{is}\:\mathrm{radius}^{\mathrm{2}} \:\mathrm{of}\:\mathrm{director}\:\mathrm{circle}\:\mathrm{and}\: \\ $$$$\mathrm{director}\:\mathrm{circle}\:\mathrm{radius}\:\mathrm{also}\:\mathrm{equal}\:\mathrm{to} \\ $$$$\mathrm{BO}…\mathrm{equate} \\ $$
Commented by rahul 19 last updated on 11/Feb/18

$${ok},\:{fine}\:. \\ $$$${thanks}!! \\ $$
